Delaunay Triangulation: Difference between revisions
Jump to navigation
Jump to search
No edit summary |
No edit summary |
||
| (4 intermediate revisions by the same user not shown) | |||
| Line 8: | Line 8: | ||
== Parameters == | == Parameters == | ||
n: number of points | $n$: number of points | ||
== Table of Algorithms == | == Table of Algorithms == | ||
| Line 18: | Line 18: | ||
|- | |- | ||
| [[ Katajainen and M. Koppinen ( Delaunay Triangulation)| Katajainen and M. Koppinen]] || | | [[Fortune ( Delaunay Triangulation)|Fortune]] || 1987 || $O(n \log n)$ || $O(n)$ || Exact || Deterministic || [http://www.wias-berlin.de/people/si/course/files/Fortune87-SweepLine-Voronoi.pdf Time] | ||
|- | |||
| [[Naive algorithm (2-Dimensional Delaunay Triangulation Delaunay Triangulation)|Naive algorithm]] || 1934 || $O(n^{4})$? (previously $O(n^{2})$) || $O(n)$ || Exact || Deterministic || | |||
|- | |||
| [[Flipping algorithm (2-Dimensional Delaunay Triangulation Delaunay Triangulation)|Flipping algorithm]] || 1999 || $O(n^{2})$ || $O(n)$ || Exact || Deterministic || [https://link.springer.com/article/10.1007/PL00009464 Time] | |||
|- | |||
| [[de Berg; Cheong (2-Dimensional Delaunay Triangulation Delaunay Triangulation)|de Berg; Cheong]] || 2008 || $O(n \log n)$ || $O(n)$ || Exact || Deterministic || [https://web.archive.org/web/20091028054315/http://www.cs.uu.nl/geobook/interpolation.pdf Time] | |||
|- | |||
| [[Bowyer–Watson algorithm (2-Dimensional Delaunay Triangulation Delaunay Triangulation)|Bowyer–Watson algorithm]] || 1981 || $O(n \log n)$ || $O(n)$ || Exact || Deterministic || [https://academic.oup.com/comjnl/article/24/2/167/338200 Time] | |||
|- | |||
| [[Belloch (2-Dimensional Delaunay Triangulation Delaunay Triangulation)|Belloch]] || 2006 || $O(n \log n)$ || $O(n)$ || Exact || Parallel || [https://web.archive.org/web/20180425231851/https://www.cs.cmu.edu/~ygu1/paper/SPAA16/Incremental.pdf Time] | |||
|- | |||
| [[Guibas; Stofli (2-Dimensional Delaunay Triangulation Delaunay Triangulation)|Guibas; Stofli]] || 1985 || $O(n \log n)$ || $O(n)$ || Exact || Deterministic || [http://www.geom.uiuc.edu/~samuelp/del_project.html Time] | |||
|- | |||
| [[Fortune (2-Dimensional Delaunay Triangulation Delaunay Triangulation)|Fortune]] || 1992 || $O(n^{2})$ || $O(n)$ || Exact || Deterministic || [https://dl.acm.org/doi/10.1145/142675.142695 Time] | |||
|- | |||
| [[S-hull (Sinclair) (2-Dimensional Delaunay Triangulation Delaunay Triangulation)|S-hull (Sinclair)]] || 2010 || $O(n \log n)$ || $O(n)$ || Exact || Deterministic || [http://www.s-hull.org/paper/s_hull.pdf Time] | |||
|- | |||
| [[Dwyer (2-Dimensional Delaunay Triangulation Delaunay Triangulation)|Dwyer]] || 1987 || $O(n \log n)$ || $O(n)$? || Exact || Deterministic || [https://link.springer.com/article/10.1007/BF01840356 Time] | |||
|- | |||
| [[ Katajainen and M. Koppinen ( Delaunay Triangulation)| Katajainen and M. Koppinen]] || 1988 || $O(n \log n)$ || || Exact || Deterministic || [https://ieeexplore.ieee.org/stamp/stamp.jsp?tp=&arnumber=6313167 Time] | |||
|- | |||
| [[Drysdale; Su (2-Dimensional Delaunay Triangulation Delaunay Triangulation)|Drysdale; Su]] || 1996 || $O(n)$ || $O(n)$? || Exact || Deterministic || [https://web.archive.org/web/20120308043808/http://www.cs.berkeley.edu/~jrs/meshpapers/SuDrysdale.pdf Time] | |||
|- | |||
| [[Dwyer (higher dimensions) (General Delaunay Triangulation (d-dimensions) Delaunay Triangulation)|Dwyer (higher dimensions)]] || 1987 || $O(n \log \log n)$ || $O(n)$? || Exact || Deterministic || [https://link.springer.com/article/10.1007/BF02574694 Time] | |||
|- | |- | ||
|} | |} | ||
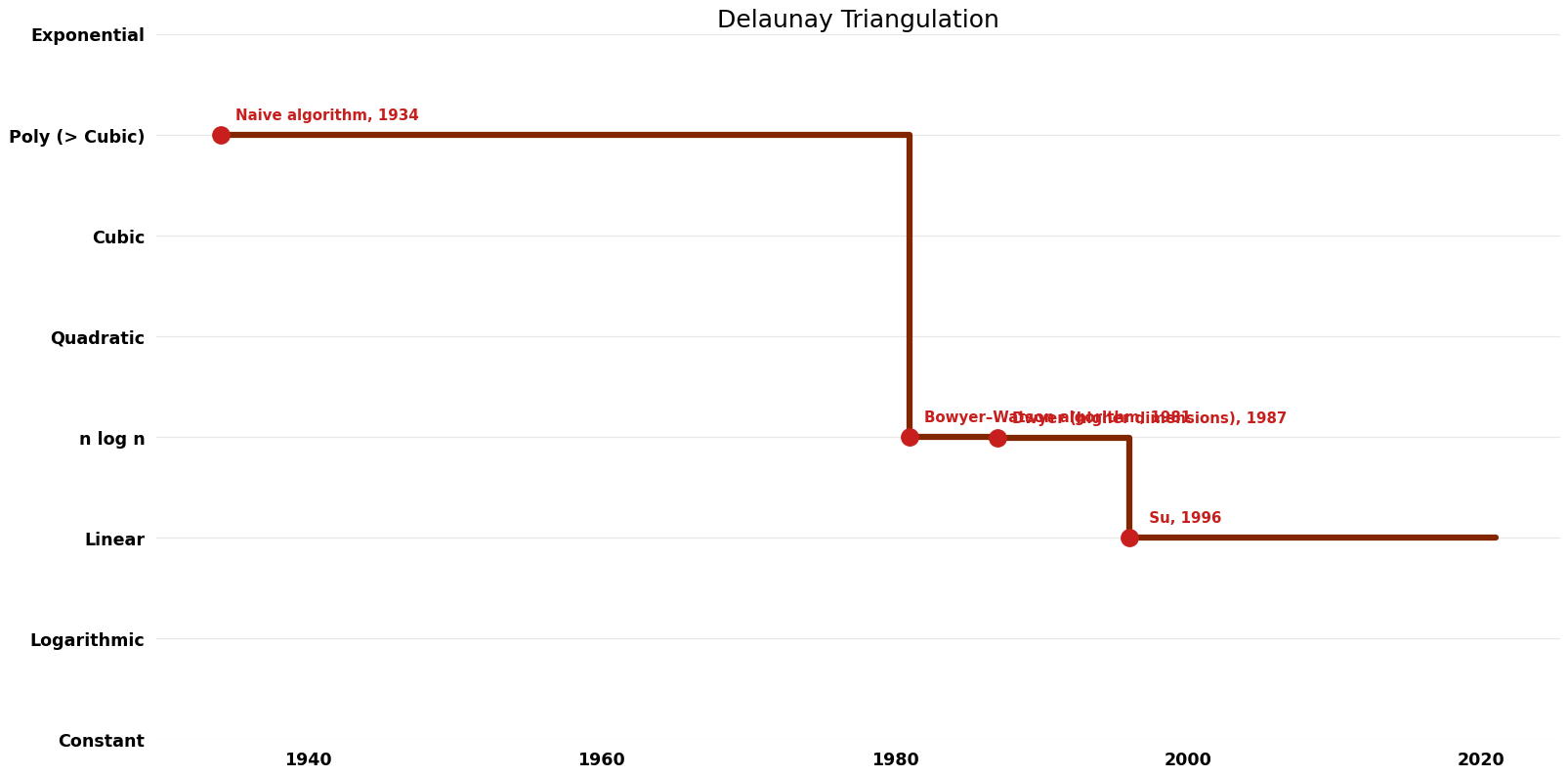
== Time Complexity | == Time Complexity Graph == | ||
[[File:Delaunay Triangulation - Time.png|1000px]] | [[File:Delaunay Triangulation - Time.png|1000px]] | ||
Latest revision as of 10:09, 28 April 2023
Description
Given a set of points, the Delaunay Triangulation problem is to triangulate the points using the following notion of triangulation.
$AB$ is an edge of the Delaunay triangulation iff there is a circle passing through $A$ and $B$ so that all other points in the point set, $C$, where $C$ is not equal to $A$ or $B$, lie outside the circle. Equivalently, all triangles in the Delaunay triangulation for a set of points will have empty circumscribed circles. That is, no points lie in the interior of any triangle's circumcircle.
Parameters
$n$: number of points
Table of Algorithms
| Name | Year | Time | Space | Approximation Factor | Model | Reference |
|---|---|---|---|---|---|---|
| Fortune | 1987 | $O(n \log n)$ | $O(n)$ | Exact | Deterministic | Time |
| Naive algorithm | 1934 | $O(n^{4})$? (previously $O(n^{2})$) | $O(n)$ | Exact | Deterministic | |
| Flipping algorithm | 1999 | $O(n^{2})$ | $O(n)$ | Exact | Deterministic | Time |
| de Berg; Cheong | 2008 | $O(n \log n)$ | $O(n)$ | Exact | Deterministic | Time |
| Bowyer–Watson algorithm | 1981 | $O(n \log n)$ | $O(n)$ | Exact | Deterministic | Time |
| Belloch | 2006 | $O(n \log n)$ | $O(n)$ | Exact | Parallel | Time |
| Guibas; Stofli | 1985 | $O(n \log n)$ | $O(n)$ | Exact | Deterministic | Time |
| Fortune | 1992 | $O(n^{2})$ | $O(n)$ | Exact | Deterministic | Time |
| S-hull (Sinclair) | 2010 | $O(n \log n)$ | $O(n)$ | Exact | Deterministic | Time |
| Dwyer | 1987 | $O(n \log n)$ | $O(n)$? | Exact | Deterministic | Time |
| Katajainen and M. Koppinen | 1988 | $O(n \log n)$ | Exact | Deterministic | Time | |
| Drysdale; Su | 1996 | $O(n)$ | $O(n)$? | Exact | Deterministic | Time |
| Dwyer (higher dimensions) | 1987 | $O(n \log \log n)$ | $O(n)$? | Exact | Deterministic | Time |