Lowest Common Ancestor: Difference between revisions
Jump to navigation
Jump to search
(Created page with "{{DISPLAYTITLE:Lowest Common Ancestor (Lowest Common Ancestor)}} == Description == Given a collection of rooted trees, answer queries of the form, "What is the nearest common ancestor of vertices $x$ and $y$?" == Related Problems == Subproblem: Off-Line Lowest Common Ancestor, Lowest Common Ancestor with Static Trees, Lowest Common Ancestor with Linking Roots, Lowest Common Ancestor with Linking, Lowest Common Ancestors with Linking and Cutting...") |
No edit summary |
||
| (4 intermediate revisions by the same user not shown) | |||
| Line 13: | Line 13: | ||
== Parameters == | == Parameters == | ||
$n$: number of vertices | |||
m: number of total number of operations (queries, links, and cuts) | |||
$m$: number of total number of operations (queries, links, and cuts) | |||
== Table of Algorithms == | == Table of Algorithms == | ||
{| class="wikitable sortable" style="text-align:center;" width="100%" | |||
== | |||
! Name !! Year !! Time !! Space !! Approximation Factor !! Model !! Reference | |||
|- | |||
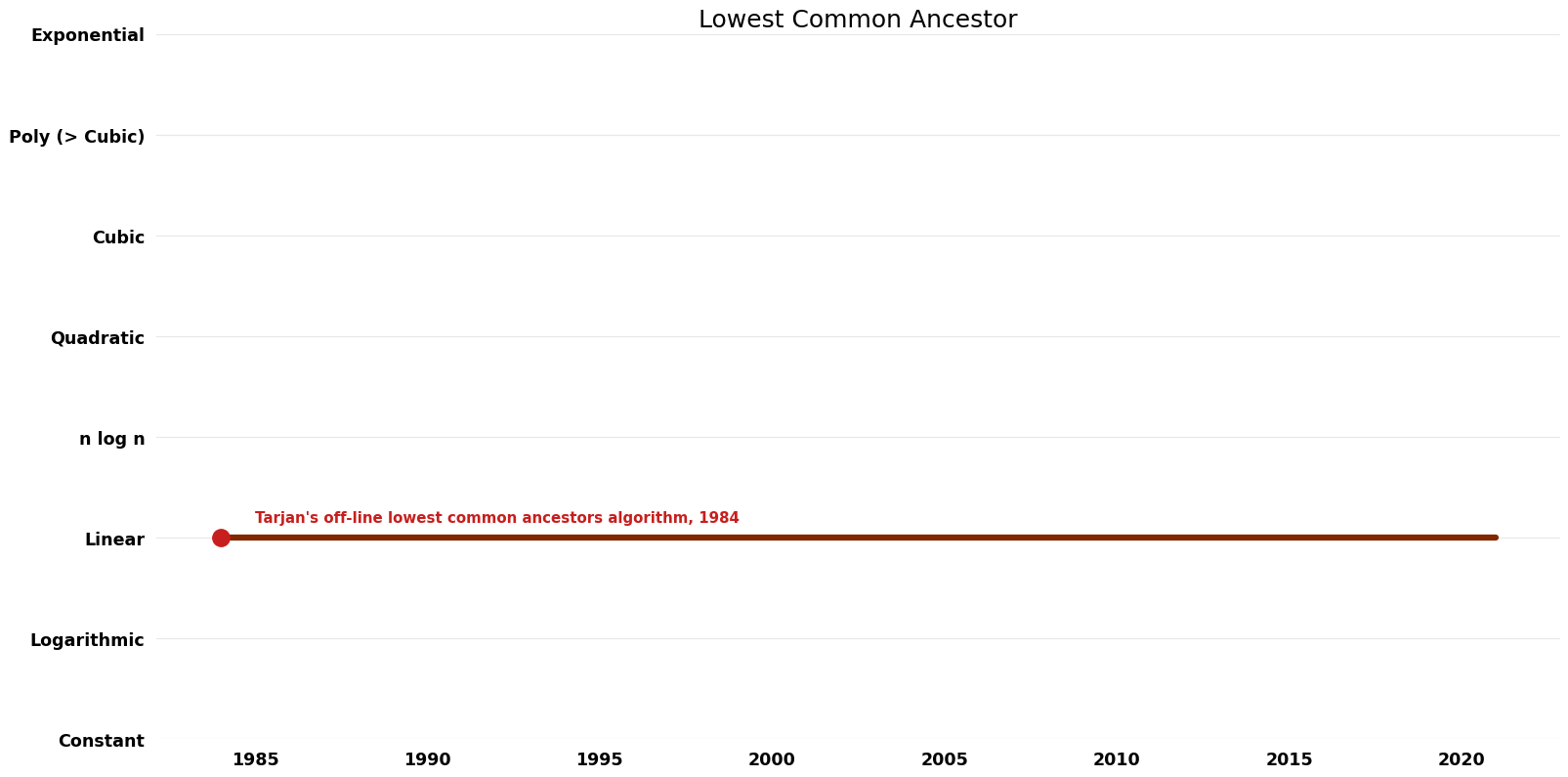
[[ | | [[Tarjan's off-line lowest common ancestors algorithm (Off-Line Lowest Common Ancestor Lowest Common Ancestor)|Tarjan's off-line lowest common ancestors algorithm]] || 1984 || $O(n+m)$ || $O(n)$ || Exact || Deterministic || [https://www.semanticscholar.org/paper/Fast-Algorithms-for-Finding-Nearest-Common-Harel-Tarjan/8867d059dda279b1aed4a0301e4e46f9daf65174 Time & Space] | ||
|- | |||
| [[Schieber; Vishkin (Lowest Common Ancestor with Static Trees Lowest Common Ancestor)|Schieber; Vishkin]] || 1988 || $O(n+m)$ || $O(n)$ || Exact || Deterministic || [https://epubs.siam.org/doi/abs/10.1137/0217079?journalCode=smjcat Time & Space] | |||
|- | |||
| [[Berkman; Vishkin (Lowest Common Ancestor with Static Trees Lowest Common Ancestor)|Berkman; Vishkin]] || 1993 || $O(n+m)$ ? || $O(n)$ || Exact || Deterministic || [https://apps.dtic.mil/dtic/tr/fulltext/u2/a227803.pdf Time] | |||
|- | |||
| [[Bender; Colton (LCA <=> RMQ) (Lowest Common Ancestor with Static Trees Lowest Common Ancestor)|Bender; Colton (LCA <=> RMQ)]] || 2000 || $O(n+m)$ || $O(n)$ || Exact || Deterministic || [https://www.ics.uci.edu/~eppstein/261/BenFar-LCA-00.pdf Time] | |||
|- | |||
| [[Stephen Alstrup, Cyril Gavoille, Haim Kaplan & Theis Rauhe (Lowest Common Ancestor with Static Trees Lowest Common Ancestor)|Stephen Alstrup, Cyril Gavoille, Haim Kaplan & Theis Rauhe ]] || 2004 || $O(n+m)$ || $O(n)$ || Exact || Deterministic || [https://link.springer.com/article/10.1007/s00224-004-1155-5 Time] | |||
|- | |||
| [[Aho, Hopcroft, and Ullman (Offline) (Off-Line Lowest Common Ancestor Lowest Common Ancestor)|Aho, Hopcroft, and Ullman (Offline)]] || 1976 || $O(n+ m*alpha(m + n, n)$) where alpha is the inverse Ackermann function || $O(n)$ || Exact || Deterministic || [https://dl.acm.org/doi/pdf/10.1145/800125.804056 Time] & [https://www.cs.bgu.ac.il/~segal/PAPERS2/tarj.pdf Space] | |||
|- | |||
| [[Aho, Hopcroft, and Ullman (Static Trees) (Lowest Common Ancestor with Static Trees Lowest Common Ancestor)|Aho, Hopcroft, and Ullman (Static Trees)]] || 1976 || $O((m+n)$*log(log(n))) || $O(n*log(log(n)$)) || Exact || Deterministic || [https://dl.acm.org/doi/pdf/10.1145/800125.804056 Time] & [https://www.cs.bgu.ac.il/~segal/PAPERS2/tarj.pdf Space] | |||
|- | |||
| [[Aho, Hopcroft, and Ullman (Linking) (Lowest Common Ancestor with Linking Lowest Common Ancestor)|Aho, Hopcroft, and Ullman (Linking)]] || 1976 || $O((m+n)$*log(n)) || $O(n*log(n)$) || Exact || Deterministic || [https://dl.acm.org/doi/pdf/10.1145/800125.804056 Time] & [https://www.cs.bgu.ac.il/~segal/PAPERS2/tarj.pdf Space] | |||
|- | |||
| [[Modified van Leeuwen (Static Trees) (Lowest Common Ancestor with Static Trees Lowest Common Ancestor)|Modified van Leeuwen (Static Trees)]] || 1976 || $O(n+m*log(log(n)$)) || $O(n)$ || Exact || Deterministic || [https://www.cs.bgu.ac.il/~segal/PAPERS2/tarj.pdf Space] | |||
|- | |||
| [[Modified van Leeuwen (Linking Roots) (Lowest Common Ancestor with Linking Roots Lowest Common Ancestor)|Modified van Leeuwen (Linking Roots)]] || 1976 || $O(n+m*log(log(n)$)) || $O(n)$ || Exact || Deterministic || [https://www.cs.bgu.ac.il/~segal/PAPERS2/tarj.pdf Space] | |||
|- | |||
| [[Sleator and Tarjan (Linking) (Lowest Common Ancestor with Linking Lowest Common Ancestor)|Sleator and Tarjan (Linking)]] || 1983 || $O(n+m*log(n)$) || $O(n)$ || Exact || Deterministic || [https://www.sciencedirect.com/science/article/pii/0022000083900065 Time] & [https://www.cs.bgu.ac.il/~segal/PAPERS2/tarj.pdf Space] | |||
|- | |||
| [[Sleator and Tarjan (Linking and Cutting) (Lowest Common Ancestor with Linking and Cutting Lowest Common Ancestor)|Sleator and Tarjan (Linking and Cutting)]] || 1983 || $O(n+m*log(n)$) || $O(n)$ || Exact || Deterministic || [https://www.sciencedirect.com/science/article/pii/0022000083900065 Time] & [https://www.cs.bgu.ac.il/~segal/PAPERS2/tarj.pdf Space] | |||
|- | |||
| [[Harel, Tarjan (Static Trees) (Lowest Common Ancestor with Static Trees Lowest Common Ancestor)|Harel, Tarjan (Static Trees)]] || 1984 || $O(n+m)$ || $O(n)$ || Exact || Deterministic || [https://www.semanticscholar.org/paper/Fast-Algorithms-for-Finding-Nearest-Common-Harel-Tarjan/8867d059dda279b1aed4a0301e4e46f9daf65174 Time] & [https://www.cs.bgu.ac.il/~segal/PAPERS2/tarj.pdf Space] | |||
|- | |||
| [[Harel, Tarjan (Linking Roots) (Lowest Common Ancestor with Linking Roots Lowest Common Ancestor)|Harel, Tarjan (Linking Roots)]] || 1984 || $O(n+ m*alpha(m + n, n)$) where alpha is the inverse Ackermann function || $O(n)$ || Exact || Deterministic || [https://www.semanticscholar.org/paper/Fast-Algorithms-for-Finding-Nearest-Common-Harel-Tarjan/8867d059dda279b1aed4a0301e4e46f9daf65174 Time] & [https://www.cs.bgu.ac.il/~segal/PAPERS2/tarj.pdf Space] | |||
|- | |||
| [[Schieber; Vishkin (Parallel) (Lowest Common Ancestor with Static Trees Lowest Common Ancestor)|Schieber; Vishkin (Parallel)]] || 1988 || $O(m+log(n)$) || $O(n)$ total (auxiliary?) || Exact || Parallel || [https://epubs.siam.org/doi/abs/10.1137/0217079?journalCode=smjcat Time] & [https://www.proquest.com/docview/919780720?pq-origsite=gscholar&fromopenview=true Space] | |||
|- | |||
| [[Fischer, Heun (Lowest Common Ancestor with Static Trees Lowest Common Ancestor)|Fischer, Heun]] || 2006 || $O(m+n)$ || $O(n)$ || Exact || Parallel || [https://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.64.5439 Time & Space] | |||
|- | |||
| [[Kmett (Lowest Common Ancestor with Static Trees Lowest Common Ancestor)|Kmett]] || 2015 || $O(m*log(h)$) || || Exact || Parallel || [https://www.schoolofhaskell.com/user/edwardk/online-lca Time] | |||
|- | |||
|} | |||
== | == Time Complexity Graph == | ||
[[File:Lowest Common Ancestor - | [[File:Lowest Common Ancestor - Time.png|1000px]] | ||
Latest revision as of 10:08, 28 April 2023
Description
Given a collection of rooted trees, answer queries of the form, "What is the nearest common ancestor of vertices $x$ and $y$?"
Related Problems
Subproblem: Off-Line Lowest Common Ancestor, Lowest Common Ancestor with Static Trees, Lowest Common Ancestor with Linking Roots, Lowest Common Ancestor with Linking, Lowest Common Ancestors with Linking and Cutting
Related: Lowest Common Ancestor with Static Trees, Lowest Common Ancestor with Linking Roots, Lowest Common Ancestor with Linking, Lowest Common Ancestors with Linking and Cutting
Parameters
$n$: number of vertices
$m$: number of total number of operations (queries, links, and cuts)
Table of Algorithms
| Name | Year | Time | Space | Approximation Factor | Model | Reference |
|---|---|---|---|---|---|---|
| Tarjan's off-line lowest common ancestors algorithm | 1984 | $O(n+m)$ | $O(n)$ | Exact | Deterministic | Time & Space |
| Schieber; Vishkin | 1988 | $O(n+m)$ | $O(n)$ | Exact | Deterministic | Time & Space |
| Berkman; Vishkin | 1993 | $O(n+m)$ ? | $O(n)$ | Exact | Deterministic | Time |
| [[Bender; Colton (LCA <=> RMQ) (Lowest Common Ancestor with Static Trees Lowest Common Ancestor)|Bender; Colton (LCA <=> RMQ)]] | 2000 | $O(n+m)$ | $O(n)$ | Exact | Deterministic | Time |
| Stephen Alstrup, Cyril Gavoille, Haim Kaplan & Theis Rauhe | 2004 | $O(n+m)$ | $O(n)$ | Exact | Deterministic | Time |
| Aho, Hopcroft, and Ullman (Offline) | 1976 | $O(n+ m*alpha(m + n, n)$) where alpha is the inverse Ackermann function | $O(n)$ | Exact | Deterministic | Time & Space |
| Aho, Hopcroft, and Ullman (Static Trees) | 1976 | $O((m+n)$*log(log(n))) | $O(n*log(log(n)$)) | Exact | Deterministic | Time & Space |
| Aho, Hopcroft, and Ullman (Linking) | 1976 | $O((m+n)$*log(n)) | $O(n*log(n)$) | Exact | Deterministic | Time & Space |
| Modified van Leeuwen (Static Trees) | 1976 | $O(n+m*log(log(n)$)) | $O(n)$ | Exact | Deterministic | Space |
| Modified van Leeuwen (Linking Roots) | 1976 | $O(n+m*log(log(n)$)) | $O(n)$ | Exact | Deterministic | Space |
| Sleator and Tarjan (Linking) | 1983 | $O(n+m*log(n)$) | $O(n)$ | Exact | Deterministic | Time & Space |
| Sleator and Tarjan (Linking and Cutting) | 1983 | $O(n+m*log(n)$) | $O(n)$ | Exact | Deterministic | Time & Space |
| Harel, Tarjan (Static Trees) | 1984 | $O(n+m)$ | $O(n)$ | Exact | Deterministic | Time & Space |
| Harel, Tarjan (Linking Roots) | 1984 | $O(n+ m*alpha(m + n, n)$) where alpha is the inverse Ackermann function | $O(n)$ | Exact | Deterministic | Time & Space |
| Schieber; Vishkin (Parallel) | 1988 | $O(m+log(n)$) | $O(n)$ total (auxiliary?) | Exact | Parallel | Time & Space |
| Fischer, Heun | 2006 | $O(m+n)$ | $O(n)$ | Exact | Parallel | Time & Space |
| Kmett | 2015 | $O(m*log(h)$) | Exact | Parallel | Time |