DFA Minimization: Difference between revisions
Jump to navigation
Jump to search
(Created page with "== Problem Description== == Bounds Chart == 350px == Step Chart == 350px == Improvement Table == {| class="wikitable" style="text-align:center;" width="100%" !width="20%" | Complexity Classes !! width="40%" | Algorithm Paper Links !! width="40%" | Lower Bounds Paper Links |- | rowspan="1" | Exp/Factorial | | |- | rowspan="1" | Polynomial > 3 | | |- | rowspan="1" | Cubic | | |- | rowspa...") |
No edit summary |
||
| (5 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
== | {{DISPLAYTITLE:DFA Minimization (DFA Minimization)}} | ||
== Description == | |||
Given a finite deterministic automaton (DFA) from a class $C$ of DFAs, determine its minimal automaton given by the equivalence relation on states. | |||
== | == Related Problems == | ||
== | Subproblem: [[Acyclic DFA Minimization]], [[ Cyclic Nontrivial SCCs DFA Minimization]] | ||
Related: [[Cyclic Nontrivial SCCs DFA Minimization]] | |||
== Parameters == | |||
$n$: number of states | |||
$d$: number of transitions | |||
$k$: size of alphabet | |||
== Table of Algorithms == | |||
{| class="wikitable sortable" style="text-align:center;" width="100%" | |||
! Name !! Year !! Time !! Space !! Approximation Factor !! Model !! Reference | |||
|- | |- | ||
| | |||
| | | [[Hopcroft's algorithm (DFA Minimization DFA Minimization)|Hopcroft's algorithm]] || 1971 || $O(kn \log n)$ || $O(kn)$ || Exact || Deterministic || [https://www.cs.cmu.edu/~./sutner/CDM/papers/Hopcroft71.pdf Time] & [https://link.springer.com/content/pdf/10.1007/3-540-54430-5_107.pdf Space] | ||
| | |||
|- | |- | ||
| | | [[Moore's algorithm (DFA Minimization DFA Minimization)|Moore's algorithm]] || 1956 || $O(n^{2} k)$ || $O(n)$ || Exact || Deterministic || [https://doi.org/10.2307/2964500 Time] | ||
| | |||
| | |||
|- | |- | ||
| | | [[Brzozowski's algorithm (DFA Minimization DFA Minimization)|Brzozowski's algorithm]] || 1963 || $O({2}^n)$ || $O({2}^n)$ || Exact || Deterministic || [https://www.semanticscholar.org/paper/Canonical-regular-expressions-and-minimal-state-for-Brzozowski/94def4233e1e8f15bab72e82708a03fd37233b14 Time] & [http://www.cs.ru.nl/bachelors-theses/2017/Erin_van_der_Veen___4431200___The_Practical_Performance_of_Automata_Minimization_Algorithms.pdf Space] | ||
| | |||
| | |||
|- | |- | ||
| | | [[Revuz's algorithm (Acyclic DFA Minimization DFA Minimization)|Revuz's algorithm]] || 1992 || $O(n)$ || $O(n)$ || Exact || Deterministic || [https://www.sciencedirect.com/science/article/pii/0304397592901423 Time] & [https://www.labri.fr/perso/zeitoun/research/pdf/Almeida-Zeitoun-IPL2008.pdf Space] | ||
| | |||
| | |||
|- | |- | ||
| | | [[Almeida & Zeitoun (Cyclic Nontrivial SCCs DFA Minimization DFA Minimization)|Almeida & Zeitoun]] || 2008 || $O(n)$ || $O(n)$ || Exact || Deterministic || [https://www.labri.fr/perso/zeitoun/research/pdf/Almeida-Zeitoun-IPL2008.pdf Time & Space] | ||
| | |||
| | |||
|- | |- | ||
| | |} | ||
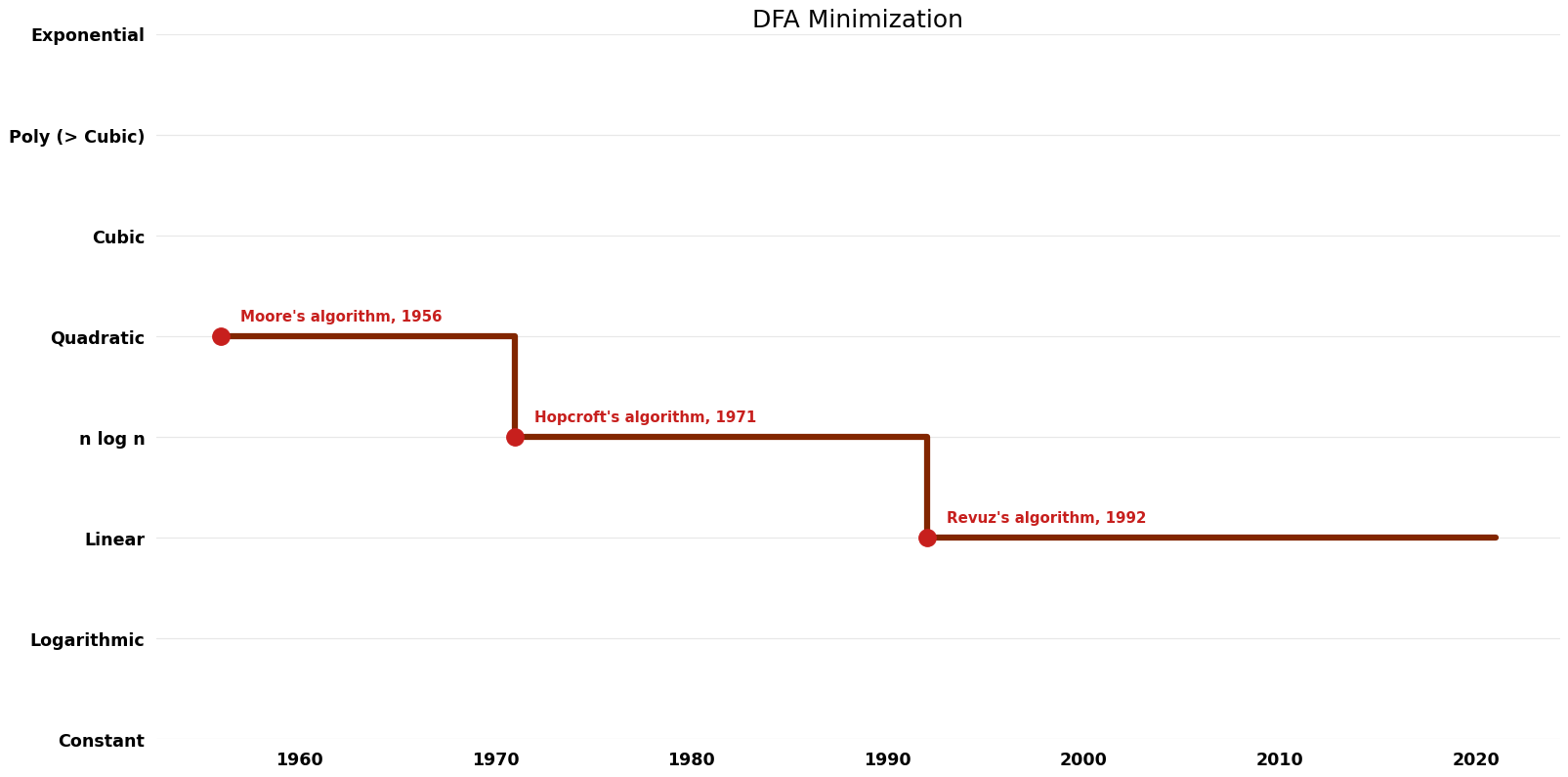
== Time Complexity Graph == | |||
[[File:DFA Minimization - Time.png|1000px]] | |||
Latest revision as of 10:08, 28 April 2023
Description
Given a finite deterministic automaton (DFA) from a class $C$ of DFAs, determine its minimal automaton given by the equivalence relation on states.
Related Problems
Subproblem: Acyclic DFA Minimization, Cyclic Nontrivial SCCs DFA Minimization
Related: Cyclic Nontrivial SCCs DFA Minimization
Parameters
$n$: number of states
$d$: number of transitions
$k$: size of alphabet
Table of Algorithms
| Name | Year | Time | Space | Approximation Factor | Model | Reference |
|---|---|---|---|---|---|---|
| Hopcroft's algorithm | 1971 | $O(kn \log n)$ | $O(kn)$ | Exact | Deterministic | Time & Space |
| Moore's algorithm | 1956 | $O(n^{2} k)$ | $O(n)$ | Exact | Deterministic | Time |
| Brzozowski's algorithm | 1963 | $O({2}^n)$ | $O({2}^n)$ | Exact | Deterministic | Time & Space |
| Revuz's algorithm | 1992 | $O(n)$ | $O(n)$ | Exact | Deterministic | Time & Space |
| Almeida & Zeitoun | 2008 | $O(n)$ | $O(n)$ | Exact | Deterministic | Time & Space |