Topological Sorting: Difference between revisions
Jump to navigation
Jump to search
No edit summary |
No edit summary |
||
| (2 intermediate revisions by the same user not shown) | |||
| Line 6: | Line 6: | ||
== Parameters == | == Parameters == | ||
V: number of vertices | $V$: number of vertices | ||
E: number of edges | $E$: number of edges | ||
== Table of Algorithms == | == Table of Algorithms == | ||
| Line 18: | Line 18: | ||
|- | |- | ||
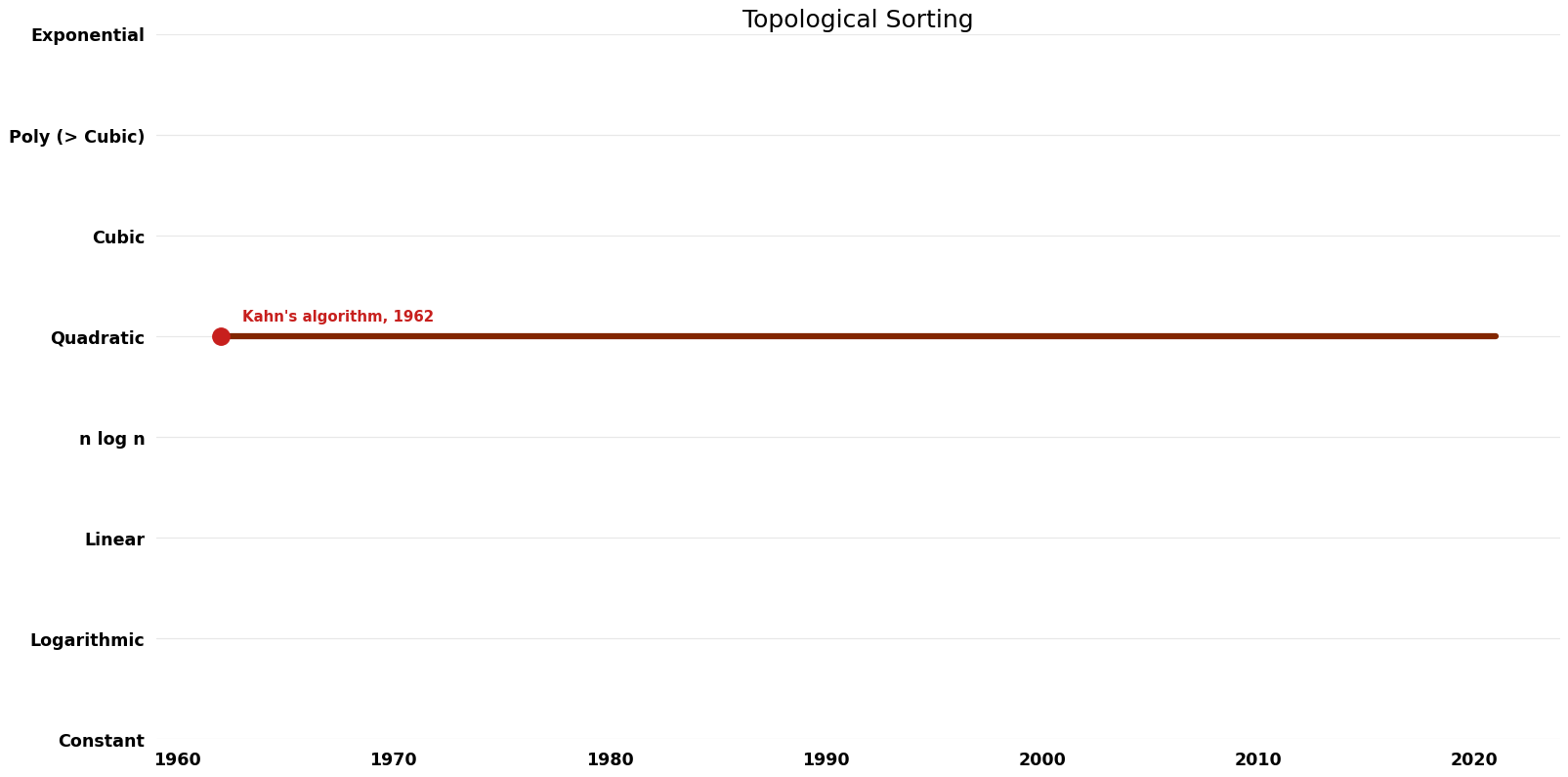
| [[Kahn's algorithm (Topological Sorting Topological Sorting)|Kahn's algorithm]] || 1962 || $O(V+E)$ || $O(V)$ | | [[Kahn's algorithm (Topological Sorting Topological Sorting)|Kahn's algorithm]] || 1962 || $O(V+E)$ || $O(V)$ || Exact || Deterministic || [https://dl.acm.org/doi/10.1145/368996.369025 Time] | ||
|- | |- | ||
| [[Tarjan's DFS based algorithm (Topological Sorting Topological Sorting)|Tarjan's DFS based algorithm]] || 1976 || $O(V+E)$ || $O(V)$ | | [[Tarjan's DFS based algorithm (Topological Sorting Topological Sorting)|Tarjan's DFS based algorithm]] || 1976 || $O(V+E)$ || $O(V)$? || Exact || Deterministic || [https://link.springer.com/article/10.1007/BF00268499 Time] | ||
|- | |- | ||
| [[Dekel; Nassimi & Sahni Parallel Implementation (Topological Sorting Topological Sorting)|Dekel; Nassimi & Sahni Parallel Implementation ]] || 1981 || $O( | | [[Dekel; Nassimi & Sahni Parallel Implementation (Topological Sorting Topological Sorting)|Dekel; Nassimi & Sahni Parallel Implementation ]] || 1981 || $O(\log^{2} V)$ || $O(V^{2})$?? || Exact || Parallel || [https://www.proquest.com/docview/920003939?pq-origsite=gscholar&fromopenview=true Time] | ||
|- | |- | ||
|} | |} | ||
| Line 29: | Line 29: | ||
[[File:Topological Sorting - Time.png|1000px]] | [[File:Topological Sorting - Time.png|1000px]] | ||
Latest revision as of 10:08, 28 April 2023
Description
Given a graph or network, find a topological sorting of the graph. A list in topological order has a special property. Simply expressed: proceeding from element to element along any path in the network, one passes through the list in one direction only. Stated another way, a list in topological order is such that no element appears in it until after all elements appearing on all paths leading to the particular element have been listed.
Parameters
$V$: number of vertices
$E$: number of edges
Table of Algorithms
| Name | Year | Time | Space | Approximation Factor | Model | Reference |
|---|---|---|---|---|---|---|
| Kahn's algorithm | 1962 | $O(V+E)$ | $O(V)$ | Exact | Deterministic | Time |
| Tarjan's DFS based algorithm | 1976 | $O(V+E)$ | $O(V)$? | Exact | Deterministic | Time |
| Dekel; Nassimi & Sahni Parallel Implementation | 1981 | $O(\log^{2} V)$ | $O(V^{2})$?? | Exact | Parallel | Time |