Variance Calculations: Difference between revisions
Jump to navigation
Jump to search
(Created page with "{{DISPLAYTITLE:Variance Calculations (Variance Calculations)}} == Description == Given a set of n (real/integer) numbers, compute the variance (sample or population). Of interest is streaming algorithms and numerical stability. == Parameters == <pre>n: number of values</pre> == Table of Algorithms == {| class="wikitable sortable" style="text-align:center;" width="100%" ! Name !! Year !! Time !! Space !! Approximation Factor !! Model !! Reference |- | Naïve...") |
No edit summary |
||
| (4 intermediate revisions by the same user not shown) | |||
| Line 6: | Line 6: | ||
== Parameters == | == Parameters == | ||
$n$: number of values | |||
== Table of Algorithms == | == Table of Algorithms == | ||
| Line 16: | Line 16: | ||
|- | |- | ||
| [[Naïve algorithm ( Variance Calculations)|Naïve algorithm]] || 1940 || $O(n)$ || $O({1})$ | | [[Naïve algorithm ( Variance Calculations)|Naïve algorithm]] || 1940 || $O(n)$ || $O({1})$ || Exact || Deterministic || | ||
|- | |- | ||
| [[Two-pass algorithm ( Variance Calculations)|Two-pass algorithm]] || 1940 || $O(n)$ || $O({1})$ | | [[Two-pass algorithm ( Variance Calculations)|Two-pass algorithm]] || 1940 || $O(n)$ || $O({1})$ || Exact || Deterministic || | ||
|- | |- | ||
| [[Welford's Online algorithm ( Variance Calculations)|Welford's Online algorithm]] || 1962 || $O(n)$ || $O({1})$ | | [[Welford's Online algorithm ( Variance Calculations)|Welford's Online algorithm]] || 1962 || $O(n)$ || $O({1})$ || Exact || Deterministic || [http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.302.7503&rep=rep1&type=pdf Time] | ||
|- | |- | ||
| [[Weighted incremental algorithm ( Variance Calculations)|Weighted incremental algorithm]] || 1979 || $O(n)$ || $O({1})$ | | [[Weighted incremental algorithm ( Variance Calculations)|Weighted incremental algorithm]] || 1979 || $O(n)$ || $O({1})$ || Exact || Deterministic || [https://dl.acm.org/doi/10.1145/359146.359153 Time] | ||
|- | |- | ||
| [[Chan's algorithm Parallel Implementation ( Variance Calculations)|Chan's algorithm Parallel Implementation]] || 1979 || $O(log n)$ || $O({1})$ per processor || Exact || Parallel || [http://i.stanford.edu/pub/cstr/reports/cs/tr/79/773/CS-TR-79-773.pdf Time] | | [[Chan's algorithm Parallel Implementation ( Variance Calculations)|Chan's algorithm Parallel Implementation]] || 1979 || $O(\log n)$ || $O({1})$ per processor || Exact || Parallel || [http://i.stanford.edu/pub/cstr/reports/cs/tr/79/773/CS-TR-79-773.pdf Time] | ||
|- | |- | ||
|} | |} | ||
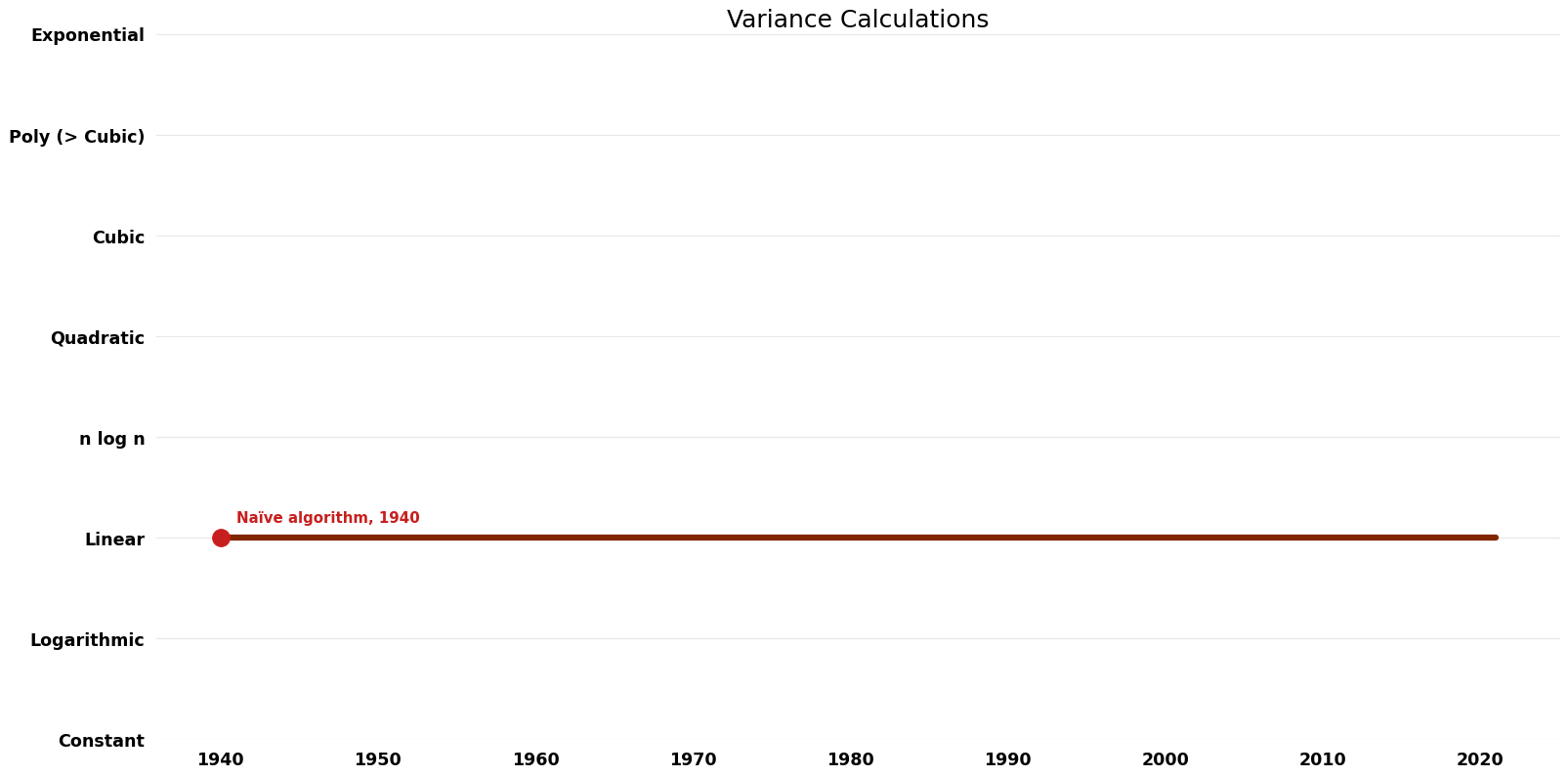
== Time Complexity | == Time Complexity Graph == | ||
[[File:Variance Calculations - Time.png|1000px]] | [[File:Variance Calculations - Time.png|1000px]] | ||
Latest revision as of 10:08, 28 April 2023
Description
Given a set of n (real/integer) numbers, compute the variance (sample or population). Of interest is streaming algorithms and numerical stability.
Parameters
$n$: number of values
Table of Algorithms
| Name | Year | Time | Space | Approximation Factor | Model | Reference |
|---|---|---|---|---|---|---|
| Naïve algorithm | 1940 | $O(n)$ | $O({1})$ | Exact | Deterministic | |
| Two-pass algorithm | 1940 | $O(n)$ | $O({1})$ | Exact | Deterministic | |
| Welford's Online algorithm | 1962 | $O(n)$ | $O({1})$ | Exact | Deterministic | Time |
| Weighted incremental algorithm | 1979 | $O(n)$ | $O({1})$ | Exact | Deterministic | Time |
| Chan's algorithm Parallel Implementation | 1979 | $O(\log n)$ | $O({1})$ per processor | Exact | Parallel | Time |