Coset Enumeration: Difference between revisions
Jump to navigation
Jump to search
No edit summary |
No edit summary |
||
| (2 intermediate revisions by the same user not shown) | |||
| Line 2: | Line 2: | ||
== Description == | == Description == | ||
Coset enumeration programs implement systematic procedures for enumerating the cosets of a subgroup H of finite index in a group G, given a set of defining relations for G and words generating H. | |||
== Parameters == | == Parameters == | ||
$n$: number of generators | |||
$g$: order of group (possibly exponential in $n$) | |||
$k$: number of relations | |||
$c$: maximum number of generators multiplied together in a relation | |||
== Table of Algorithms == | == Table of Algorithms == | ||
{| class="wikitable sortable" style="text-align:center;" width="100%" | |||
== | |||
! Name !! Year !! Time !! Space !! Approximation Factor !! Model !! Reference | |||
|- | |||
[[ | | [[Todd–Coxeter algorithm (Coset Enumeration Coset Enumeration)|Todd–Coxeter algorithm]] || 1936 || $O({2}^n)$ || $O(gkc)$ || Exact || Deterministic || [https://www.cambridge.org/core/journals/proceedings-of-the-edinburgh-mathematical-society/article/practical-method-for-enumerating-cosets-of-a-finite-abstract-group/0306574AD958F694A0A8339338348AA1 Time] | ||
|- | |||
| [[Haselgrove-Leech-Trotter (HLT) algorithm (Coset Enumeration Coset Enumeration)|Haselgrove-Leech-Trotter (HLT) algorithm]] || 1940 || $O({2}^n)$ || $O(ng)$? || Exact || Deterministic || | |||
|- | |||
| [[Knuth–Bendix algorithm (Coset Enumeration Coset Enumeration)|Knuth–Bendix algorithm]] || 1970 || $O({1.5}^n n^{2} logn)$ || $O(ng)$??? || Exact || Deterministic || [https://www.cs.tufts.edu/~nr/cs257/archive/don-knuth/knuth-bendix.pdf Time] | |||
|- | |||
|} | |||
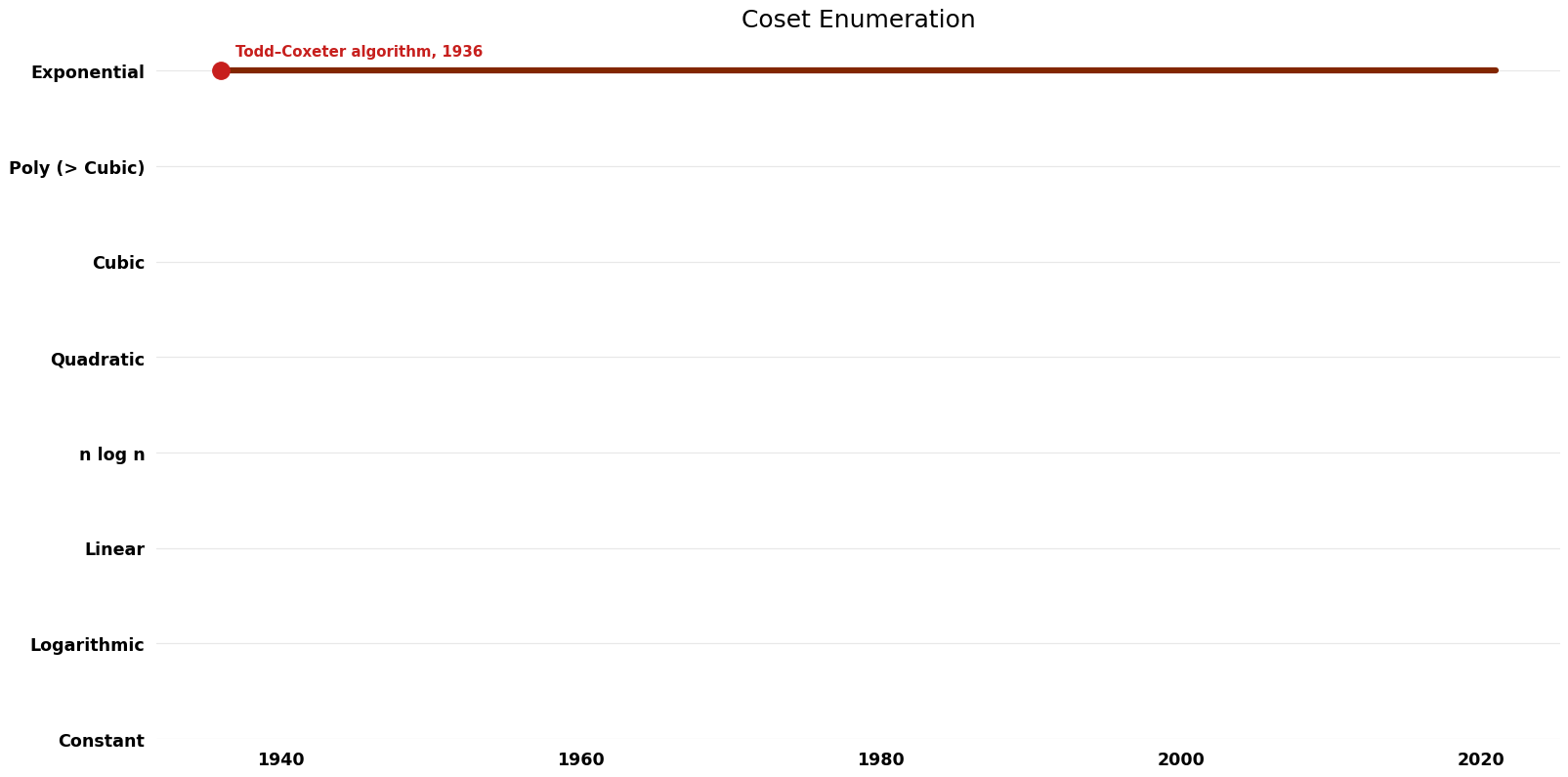
== | == Time Complexity Graph == | ||
[[File:Coset Enumeration - | [[File:Coset Enumeration - Time.png|1000px]] | ||
Latest revision as of 10:08, 28 April 2023
Description
Coset enumeration programs implement systematic procedures for enumerating the cosets of a subgroup H of finite index in a group G, given a set of defining relations for G and words generating H.
Parameters
$n$: number of generators
$g$: order of group (possibly exponential in $n$)
$k$: number of relations
$c$: maximum number of generators multiplied together in a relation
Table of Algorithms
| Name | Year | Time | Space | Approximation Factor | Model | Reference |
|---|---|---|---|---|---|---|
| Todd–Coxeter algorithm | 1936 | $O({2}^n)$ | $O(gkc)$ | Exact | Deterministic | Time |
| Haselgrove-Leech-Trotter (HLT) algorithm | 1940 | $O({2}^n)$ | $O(ng)$? | Exact | Deterministic | |
| Knuth–Bendix algorithm | 1970 | $O({1.5}^n n^{2} logn)$ | $O(ng)$??? | Exact | Deterministic | Time |