Maximum-Weight Matching: Difference between revisions
Jump to navigation
Jump to search
(Created page with "{{DISPLAYTITLE:Maximum-Weight Matching (Maximum-Weight Matching)}} == Description == In computer science, the maximum weight matching problem is the problem of finding, in a weighted graph, a matching in which the sum of weights is maximized. Here, the graph is unrestricted; i.e. can be any general graph. == Related Problems == Subproblem: Bipartite Maximum-Weight Matching == Parameters == <pre>n: number of vertices m: number of edges N: largest weight magnit...") |
No edit summary |
||
| (5 intermediate revisions by the same user not shown) | |||
| Line 10: | Line 10: | ||
== Parameters == | == Parameters == | ||
$n$: number of vertices | |||
m: number of edges | |||
N: largest weight magnitude | $m$: number of edges | ||
$N$: largest weight magnitude | |||
== Table of Algorithms == | == Table of Algorithms == | ||
| Line 22: | Line 24: | ||
|- | |- | ||
| [[Hungarian algorithm (Bipartite Maximum-Weight Matching Maximum-Weight Matching)|Hungarian algorithm]] || 1955 || $O(n^{4})$ || $O(n^{2})$ || Exact || Deterministic || [https://web.eecs.umich.edu/~pettie/matching/Kuhn-hungarian-assignment.pdf Time] | |||
|- | |||
| [[Edmonds (Maximum-Weight Matching Maximum-Weight Matching)|Edmonds]] || 1965 || $O(mn^{2})$ || $O(mn^{2})$?? || Exact || Deterministic || [https://nvlpubs.nist.gov/nistpubs/jres/69B/jresv69Bn1-2p125_A1b.pdf Time] | | [[Edmonds (Maximum-Weight Matching Maximum-Weight Matching)|Edmonds]] || 1965 || $O(mn^{2})$ || $O(mn^{2})$?? || Exact || Deterministic || [https://nvlpubs.nist.gov/nistpubs/jres/69B/jresv69Bn1-2p125_A1b.pdf Time] | ||
|- | |- | ||
| [[Micali; Vazirani ( Maximum-Weight Matching)|Micali; Vazirani]] || 1980 || $O(n^{3} | | [[Micali; Vazirani ( Maximum-Weight Matching)|Micali; Vazirani]] || 1980 || $O(n^{3} \log n)$ || || Exact || Deterministic || [https://ieeexplore.ieee.org/document/4567800 Time] | ||
|- | |- | ||
| [[Mucha and Sankowski ( Maximum-Weight Matching)|Mucha and Sankowski]] || 2004 || $O(n^{3})$ || || Exact || Deterministic || [https://dl.acm.org/doi/10.1109/FOCS.2004.40 Time] | | [[Mucha and Sankowski ( Maximum-Weight Matching)|Mucha and Sankowski]] || 2004 || $O(n^{3})$ || || Exact || Deterministic || [https://dl.acm.org/doi/10.1109/FOCS.2004.40 Time] | ||
| Line 30: | Line 34: | ||
|} | |} | ||
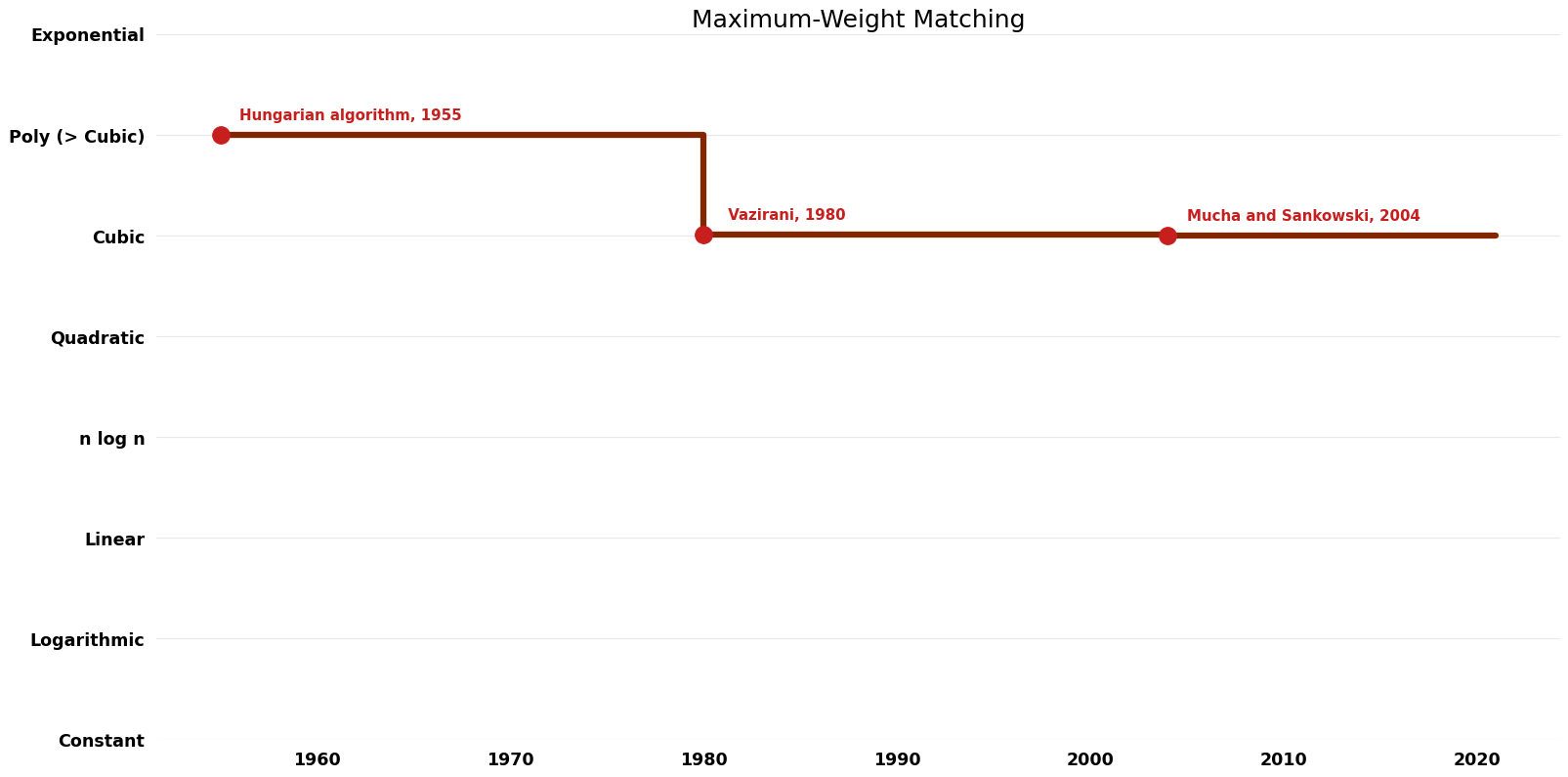
== Time Complexity | == Time Complexity Graph == | ||
[[File:Maximum-Weight Matching - Time.png|1000px]] | [[File:Maximum-Weight Matching - Time.png|1000px]] | ||
Latest revision as of 10:08, 28 April 2023
Description
In computer science, the maximum weight matching problem is the problem of finding, in a weighted graph, a matching in which the sum of weights is maximized. Here, the graph is unrestricted; i.e. can be any general graph.
Related Problems
Subproblem: Bipartite Maximum-Weight Matching
Parameters
$n$: number of vertices
$m$: number of edges
$N$: largest weight magnitude
Table of Algorithms
| Name | Year | Time | Space | Approximation Factor | Model | Reference |
|---|---|---|---|---|---|---|
| Hungarian algorithm | 1955 | $O(n^{4})$ | $O(n^{2})$ | Exact | Deterministic | Time |
| Edmonds | 1965 | $O(mn^{2})$ | $O(mn^{2})$?? | Exact | Deterministic | Time |
| Micali; Vazirani | 1980 | $O(n^{3} \log n)$ | Exact | Deterministic | Time | |
| Mucha and Sankowski | 2004 | $O(n^{3})$ | Exact | Deterministic | Time |