Alphabetic Tree Problem: Difference between revisions
Jump to navigation
Jump to search
No edit summary |
No edit summary |
||
| (2 intermediate revisions by the same user not shown) | |||
| Line 12: | Line 12: | ||
== Parameters == | == Parameters == | ||
n: number of elements | $n$: number of elements | ||
== Table of Algorithms == | == Table of Algorithms == | ||
| Line 33: | Line 33: | ||
[[File:Optimal Binary Search Trees - Alphabetic Tree Problem - Time.png|1000px]] | [[File:Optimal Binary Search Trees - Alphabetic Tree Problem - Time.png|1000px]] | ||
Latest revision as of 09:08, 28 April 2023
Description
A variant of the OBST problem is when only the gaps have nonzero access probabilities, and is called the optimal alphabetic tree problem.
Related Problems
Generalizations: Optimal Binary Search Tree Problem
Related: Approximate OBST, Huffman Encoding
Parameters
$n$: number of elements
Table of Algorithms
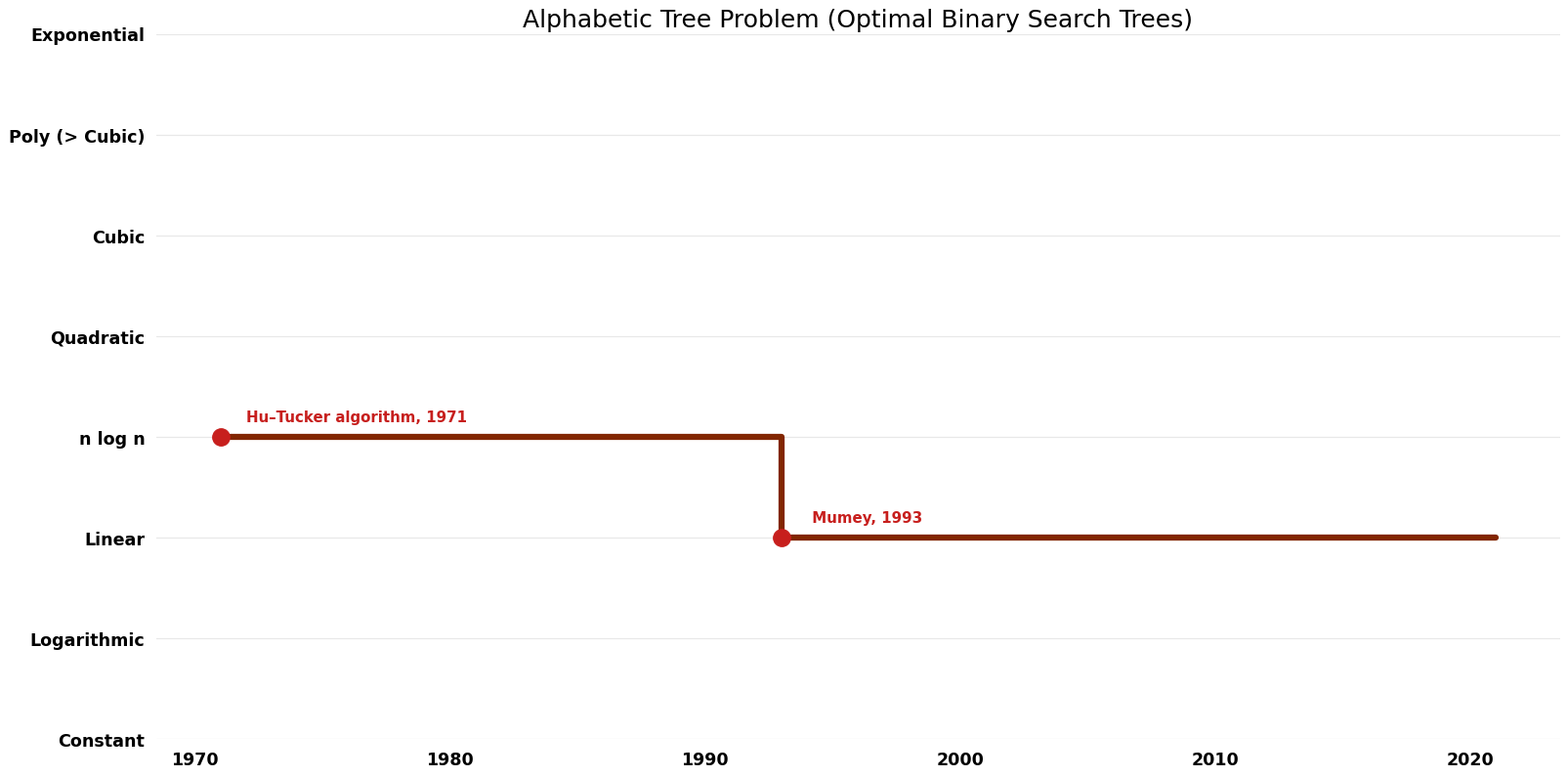
| Name | Year | Time | Space | Approximation Factor | Model | Reference |
|---|---|---|---|---|---|---|
| Klawe; Mumey | 1993 | $O(n)$ | $O(n)$ | Exact | Deterministic | Time |
| Garsia–Wachs algorithm | 1977 | $O(n \log n)$ | $O(n)$ | Exact | Deterministic | Time & Space |
| Hu–Tucker algorithm | 1971 | $O(n \log n)$ | $O(n)$ | Exact | Deterministic | Time & Space |
Time Complexity Graph
