General Graph MCM: Difference between revisions
Jump to navigation
Jump to search
(Created page with "{{DISPLAYTITLE:General Graph MCM (Maximum Cardinality Matching)}} == Description == The goal of maximum cardinality matching is to find a matching with as many edges as possible (equivalently: a matching that covers as many vertices as possible). Here, the graph can be any general graph. == Related Problems == Subproblem: Bipartite Graph MCM Related: Planar Bipartite Graph Perfect Matching == Parameters == <pre>V: number of vertices E: number of edges</p...") |
No edit summary |
||
| (5 intermediate revisions by the same user not shown) | |||
| Line 12: | Line 12: | ||
== Parameters == | == Parameters == | ||
$V$: number of vertices | |||
E: number of edges | |||
$E$: number of edges | |||
== Table of Algorithms == | == Table of Algorithms == | ||
| Line 23: | Line 24: | ||
|- | |- | ||
| [[Micali and Vazirani ( Maximum Cardinality Matching)|Micali and Vazirani]] || 1980 || $O(V^{0.5} E)$ || $O(V)$ || || Deterministic || [https:// | | [[Micali and Vazirani ( Maximum Cardinality Matching)|Micali and Vazirani]] || 1980 || $O(V^{0.5} E)$ || $O(V)$ || || Deterministic || [https://ieeexplore.ieee.org/document/4567800 Time] & [https://link.springer.com/content/pdf/10.1007/PL00009186.pdf Space] | ||
|- | |- | ||
| [[Blum (General Graph MCM Maximum Cardinality Matching)|Blum]] || 1990 || $O((V^{0.5})$E) || $O(E)$ | | [[Blum (General Graph MCM Maximum Cardinality Matching)|Blum]] || 1990 || $O((V^{0.5})$E) || $O(E)$?? || Exact || Deterministic || [https://web.eecs.umich.edu/~pettie/matching/Blum-matching-ICALP90.pdf Time] | ||
|- | |- | ||
| [[Gabow; Tarjan (General Graph MCM Maximum Cardinality Matching)|Gabow; Tarjan]] || 1991 || $O((V^{0.5})$E) || $O(E)$ | | [[Gabow; Tarjan (General Graph MCM Maximum Cardinality Matching)|Gabow; Tarjan]] || 1991 || $O((V^{0.5})$E) || $O(E)$? || Exact || Deterministic || [https://web.eecs.umich.edu/~pettie/matching/Gabow-Tarjan-scaling-general-graph-matching.pdf Time & Space] | ||
|- | |- | ||
| [[Mucha, Sankowski (general) (General Graph MCM Maximum Cardinality Matching)|Mucha, Sankowski (general)]] || 2004 || $O(V^{2.{37}6})$ || $O(V^{2})$?? || Exact || Randomized || [https://ieeexplore.ieee.org/document/1366244 Time] | | [[Mucha, Sankowski (general) (General Graph MCM Maximum Cardinality Matching)|Mucha, Sankowski (general)]] || 2004 || $O(V^{2.{37}6})$ || $O(V^{2})$?? || Exact || Randomized || [https://ieeexplore.ieee.org/document/1366244 Time] | ||
| Line 33: | Line 34: | ||
|} | |} | ||
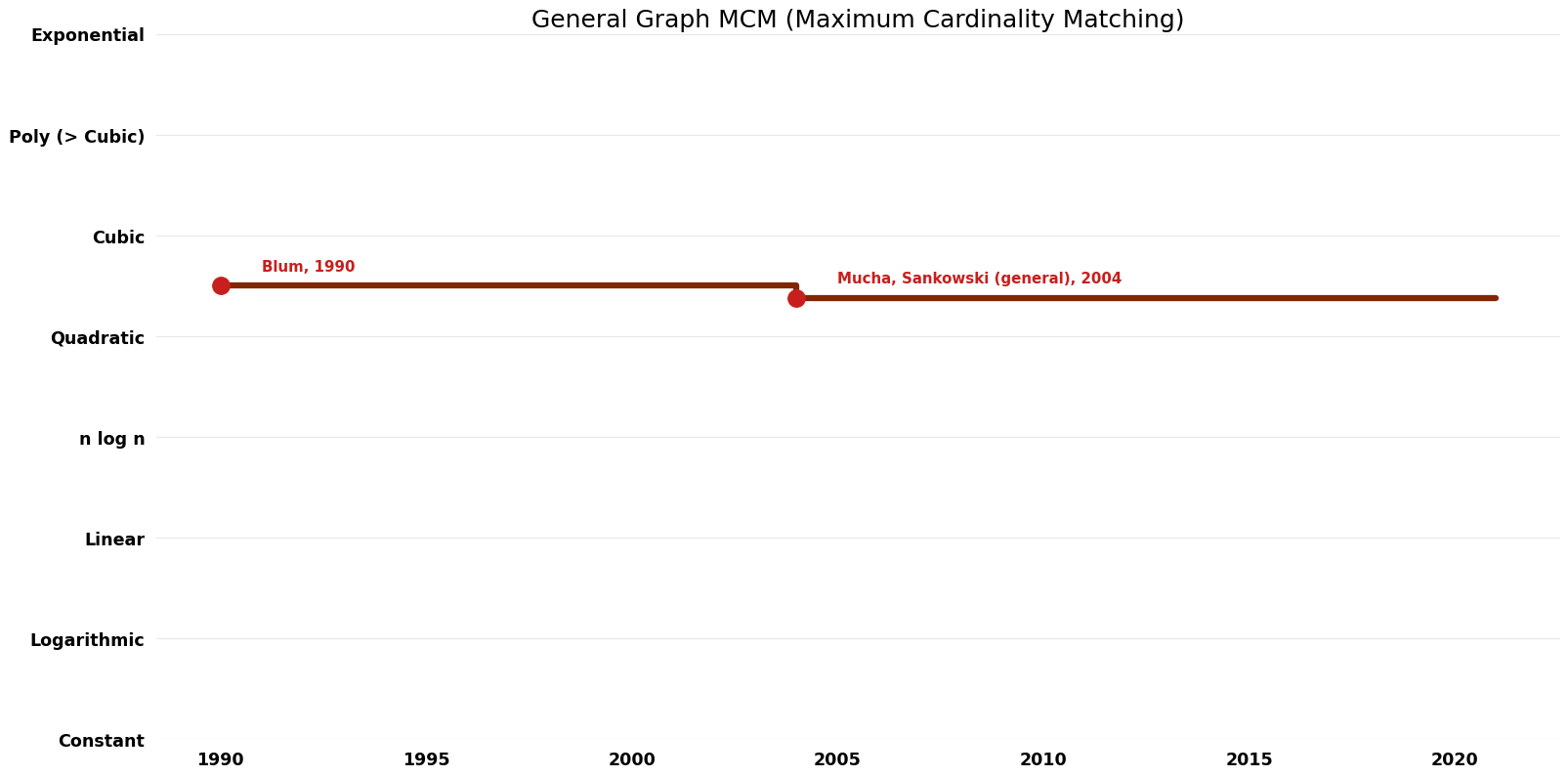
== Time Complexity | == Time Complexity Graph == | ||
[[File:Maximum Cardinality Matching - General Graph MCM - Time.png|1000px]] | [[File:Maximum Cardinality Matching - General Graph MCM - Time.png|1000px]] | ||
Latest revision as of 10:07, 28 April 2023
Description
The goal of maximum cardinality matching is to find a matching with as many edges as possible (equivalently: a matching that covers as many vertices as possible). Here, the graph can be any general graph.
Related Problems
Subproblem: Bipartite Graph MCM
Related: Planar Bipartite Graph Perfect Matching
Parameters
$V$: number of vertices
$E$: number of edges
Table of Algorithms
| Name | Year | Time | Space | Approximation Factor | Model | Reference |
|---|---|---|---|---|---|---|
| Micali and Vazirani | 1980 | $O(V^{0.5} E)$ | $O(V)$ | Deterministic | Time & Space | |
| Blum | 1990 | $O((V^{0.5})$E) | $O(E)$?? | Exact | Deterministic | Time |
| Gabow; Tarjan | 1991 | $O((V^{0.5})$E) | $O(E)$? | Exact | Deterministic | Time & Space |
| Mucha, Sankowski (general) | 2004 | $O(V^{2.{37}6})$ | $O(V^{2})$?? | Exact | Randomized | Time |