Multiplication: Difference between revisions
Jump to navigation
Jump to search
No edit summary |
No edit summary |
||
| (One intermediate revision by the same user not shown) | |||
| Line 6: | Line 6: | ||
== Parameters == | == Parameters == | ||
n: length of one of the integers, in bits | $n$: length of one of the integers, in bits | ||
== Table of Algorithms == | == Table of Algorithms == | ||
| Line 16: | Line 16: | ||
|- | |- | ||
| [[Karatsuba Algorithm ( Multiplication)|Karatsuba Algorithm]] || 1962 || $O(n^{1.{5}8})$ || $O(n)$ | | [[Karatsuba Algorithm ( Multiplication)|Karatsuba Algorithm]] || 1962 || $O(n^{1.{5}8})$ || $O(n)$ || Exact || Deterministic || [http://www.mathnet.ru/php/archive.phtml?wshow=paper&jrnid=dan&paperid=26729&option_lang=eng Time] | ||
|- | |- | ||
| [[Toom-3 ( Multiplication)|Toom-3]] || 1969 || $O(n^{1.{4}6})$ || $O(n)$ | | [[Toom-3 ( Multiplication)|Toom-3]] || 1969 || $O(n^{1.{4}6})$ || $O(n)$ || Exact || Deterministic || [https://www.ams.org/journals/tran/1969-142-00/S0002-9947-1969-0249212-8/S0002-9947-1969-0249212-8.pdf Time] | ||
|- | |- | ||
| [[Long Multiplication ( Multiplication)|Long Multiplication]] || 1940 || $O(n^{2})$ || $O(n)$ | | [[Long Multiplication ( Multiplication)|Long Multiplication]] || 1940 || $O(n^{2})$ || $O(n)$ || Exact || Deterministic || | ||
|- | |- | ||
| [[Schönhage–Strassen algorithm ( Multiplication)|Schönhage–Strassen algorithm]] || 1971 || $O(n | | [[Schönhage–Strassen algorithm ( Multiplication)|Schönhage–Strassen algorithm]] || 1971 || $O(n \log n \log\log n)$ || $O(n)$ auxiliary? || Exact || Deterministic || [https://link.springer.com/article/10.1007/BF02242355 Time] | ||
|- | |- | ||
| [[Furer's algorithm ( Multiplication)|Furer's algorithm]] || 2007 || $O( | | [[Furer's algorithm ( Multiplication)|Furer's algorithm]] || 2007 || $O(n \log n {2}^{O(\log*n)})$ || $O(n)$ auxiliary? || Exact || Deterministic || [https://web.archive.org/web/20130425232048/http://www.cse.psu.edu/~furer/Papers/mult.pdf Time] | ||
|- | |- | ||
| [[De ( Multiplication)|De]] || 2008 || $O( | | [[De ( Multiplication)|De]] || 2008 || $O(n \log n {2}^{O(\log*n)})$ || $O(n)$ auxiliary? || Exact || Deterministic || [https://arxiv.org/abs/0801.1416 Time] | ||
|- | |- | ||
| [[Harvey; Hoeven ( Multiplication)|Harvey; Hoeven]] || 2019 || $O( | | [[Harvey; Hoeven ( Multiplication)|Harvey; Hoeven]] || 2019 || $O(n \log n)$ || $O(n)$ auxiliary?? || Exact || Deterministic || [https://hal.archives-ouvertes.fr/hal-02070778 Time] | ||
|- | |- | ||
| [[Harvey; Hoeven; Lecerf ( Multiplication)|Harvey; Hoeven; Lecerf]] || 2015 || $O( | | [[Harvey; Hoeven; Lecerf ( Multiplication)|Harvey; Hoeven; Lecerf]] || 2015 || $O(n \log n {2}^{({3} \log*n)})$ || $O(n)$ auxiliary?? || Exact || Deterministic || [https://arxiv.org/abs/1407.3360 Time] | ||
|- | |- | ||
| [[Covanov and Thomé ( Multiplication)|Covanov and Thomé]] || 2015 || $O( | | [[Covanov and Thomé ( Multiplication)|Covanov and Thomé]] || 2015 || $O(n \log n {2}^{O(\log*n)})$ || $O(n)$ auxiliary?? || Exact || Deterministic || [https://hal.inria.fr/hal-01108166v1/document Time] | ||
|- | |- | ||
| [[Covanov and Thomé ( Multiplication)|Covanov and Thomé]] || 2016 || $O( | | [[Covanov and Thomé ( Multiplication)|Covanov and Thomé]] || 2016 || $O(n \log n {2}^{({3} \log*n)})$ || $O(n)$ auxiliary?? || Exact || Deterministic || [https://arxiv.org/abs/1502.02800 Time] | ||
|- | |- | ||
| [[Harvey; Hoeven; Lecerf ( Multiplication)|Harvey; Hoeven; Lecerf]] || 2018 || $O( | | [[Harvey; Hoeven; Lecerf ( Multiplication)|Harvey; Hoeven; Lecerf]] || 2018 || $O(n \log n {2}^{({2} \log*n)})$ || $O(n)$ auxiliary?? || Exact || Deterministic || [https://arxiv.org/abs/1802.07932 Time] | ||
|- | |- | ||
|} | |} | ||
| Line 43: | Line 43: | ||
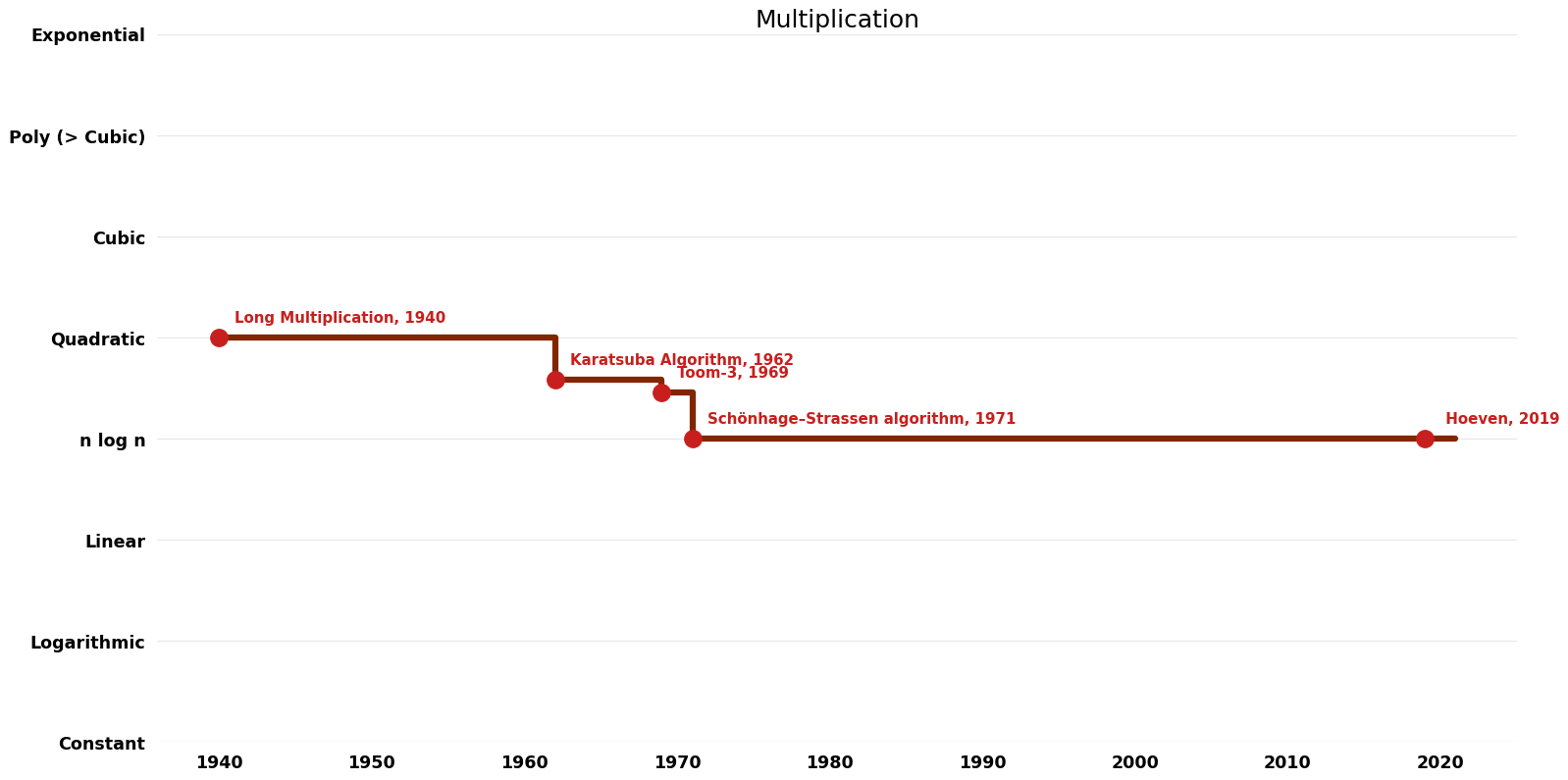
[[File:Multiplication - Time.png|1000px]] | [[File:Multiplication - Time.png|1000px]] | ||
== References/Citation == | == References/Citation == | ||
https://hal.archives-ouvertes.fr/hal-02070778 | https://hal.archives-ouvertes.fr/hal-02070778 | ||
Latest revision as of 10:07, 28 April 2023
Description
Multiplication is one of the four elementary mathematical operations of arithmetic; with the others being addition; subtraction and division. Given two $n$-bit integers, compute their product, which should be a $2n$-bit integer.
Parameters
$n$: length of one of the integers, in bits
Table of Algorithms
| Name | Year | Time | Space | Approximation Factor | Model | Reference |
|---|---|---|---|---|---|---|
| Karatsuba Algorithm | 1962 | $O(n^{1.{5}8})$ | $O(n)$ | Exact | Deterministic | Time |
| Toom-3 | 1969 | $O(n^{1.{4}6})$ | $O(n)$ | Exact | Deterministic | Time |
| Long Multiplication | 1940 | $O(n^{2})$ | $O(n)$ | Exact | Deterministic | |
| Schönhage–Strassen algorithm | 1971 | $O(n \log n \log\log n)$ | $O(n)$ auxiliary? | Exact | Deterministic | Time |
| Furer's algorithm | 2007 | $O(n \log n {2}^{O(\log*n)})$ | $O(n)$ auxiliary? | Exact | Deterministic | Time |
| De | 2008 | $O(n \log n {2}^{O(\log*n)})$ | $O(n)$ auxiliary? | Exact | Deterministic | Time |
| Harvey; Hoeven | 2019 | $O(n \log n)$ | $O(n)$ auxiliary?? | Exact | Deterministic | Time |
| Harvey; Hoeven; Lecerf | 2015 | $O(n \log n {2}^{({3} \log*n)})$ | $O(n)$ auxiliary?? | Exact | Deterministic | Time |
| Covanov and Thomé | 2015 | $O(n \log n {2}^{O(\log*n)})$ | $O(n)$ auxiliary?? | Exact | Deterministic | Time |
| Covanov and Thomé | 2016 | $O(n \log n {2}^{({3} \log*n)})$ | $O(n)$ auxiliary?? | Exact | Deterministic | Time |
| Harvey; Hoeven; Lecerf | 2018 | $O(n \log n {2}^{({2} \log*n)})$ | $O(n)$ auxiliary?? | Exact | Deterministic | Time |