Square Matrix LU Decomposition: Difference between revisions
Jump to navigation
Jump to search
No edit summary |
No edit summary |
||
| (One intermediate revision by the same user not shown) | |||
| Line 28: | Line 28: | ||
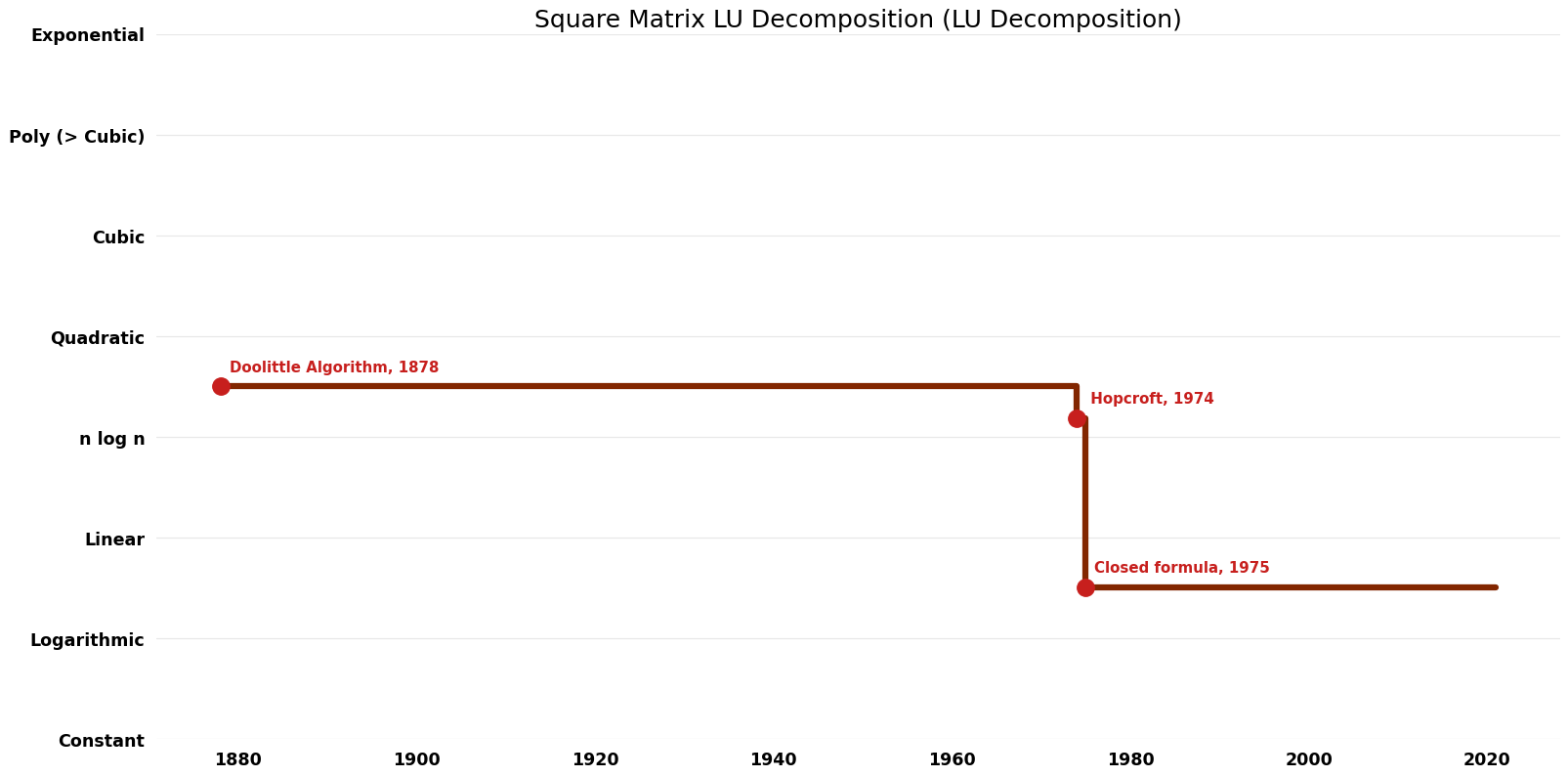
| [[Bunch; Hopcroft (Square Matrix LU Decomposition LU Decomposition)|Bunch; Hopcroft]] || 1974 || $O(n^{2.{37}6})$ || $\tilde{O}(n^{2})$ || Exact || Deterministic || [https://dl.acm.org/citation.cfm?id=248979 Time] | | [[Bunch; Hopcroft (Square Matrix LU Decomposition LU Decomposition)|Bunch; Hopcroft]] || 1974 || $O(n^{2.{37}6})$ || $\tilde{O}(n^{2})$ || Exact || Deterministic || [https://dl.acm.org/citation.cfm?id=248979 Time] | ||
|- | |- | ||
| [[Closed formula ( LU Decomposition)|Closed formula]] || 1975 || $O( | | [[Closed formula (Square Matrix LU Decomposition LU Decomposition)|Closed formula]] || 1975 || $O(n \log n)$ || || Exact || Deterministic || | ||
|- | |- | ||
| [[David ( LU Decomposition)|David]] || 2006 || $O( | | [[David (Square Matrix LU Decomposition LU Decomposition)|David]] || 2006 || $O(n \log n)$ || || Exact || Deterministic || | ||
|- | |- | ||
| [[Press, Teukolsky, Flannery (Square Matrix LU Decomposition LU Decomposition)|Press, Teukolsky, Flannery]] || 2007 || $O(n^{3})$ || $\tilde{O}(n)$ || Exact || Deterministic || [https://books.google.com/books?hl=en&lr=&id=1aAOdzK3FegC&oi=fnd&pg=PA1&dq=Teukolsky | | [[Press, Teukolsky, Flannery (Square Matrix LU Decomposition LU Decomposition)|Press, Teukolsky, Flannery]] || 2007 || $O(n^{3})$ || $\tilde{O}(n)$ || Exact || Deterministic || [https://books.google.com/books?hl=en&lr=&id=1aAOdzK3FegC&oi=fnd&pg=PA1&dq=Teukolsky#v=onepage&q=Teukolsky&f=false Time] | ||
|- | |- | ||
|} | |} | ||
| Line 39: | Line 39: | ||
[[File:LU Decomposition - Square Matrix LU Decomposition - Time.png|1000px]] | [[File:LU Decomposition - Square Matrix LU Decomposition - Time.png|1000px]] | ||
Latest revision as of 10:07, 28 April 2023
Description
Lower–upper (LU) decomposition or factorization factors a matrix as the product of a lower triangular matrix and an upper triangular matrix. In this specific case, the input is a square $n \times n$ matrix
Related Problems
Generalizations: Rectangular Matrix LU Decomposition
Parameters
$n$: dimension of square matrix
Table of Algorithms
| Name | Year | Time | Space | Approximation Factor | Model | Reference |
|---|---|---|---|---|---|---|
| Doolittle Algorithm | 1878 | $O(n^{3})$ | $\tilde{O}({1})$ | Exact | Deterministic | |
| Crout and LUP algorithms | 2007 | $O(n^{3})$ | $\tilde{O}({1})$ | Exact | Deterministic | Time |
| Okunev; Johnson | 1997 | $O(n^{3})$ | $O({1})$ | Exact | Deterministic | Time |
| Bunch; Hopcroft | 1974 | $O(n^{2.{37}6})$ | $\tilde{O}(n^{2})$ | Exact | Deterministic | Time |
| Closed formula | 1975 | $O(n \log n)$ | Exact | Deterministic | ||
| David | 2006 | $O(n \log n)$ | Exact | Deterministic | ||
| Press, Teukolsky, Flannery | 2007 | $O(n^{3})$ | $\tilde{O}(n)$ | Exact | Deterministic | Time |