Nonnegative Weights: Difference between revisions
No edit summary |
No edit summary |
||
| (One intermediate revision by the same user not shown) | |||
| Line 14: | Line 14: | ||
== Parameters == | == Parameters == | ||
V: number of vertices | $V$: number of vertices | ||
E: number of edges | $E$: number of edges | ||
L: maximum absolute value of edge cost | $L$: maximum absolute value of edge cost | ||
== Table of Algorithms == | == Table of Algorithms == | ||
| Line 28: | Line 28: | ||
|- | |- | ||
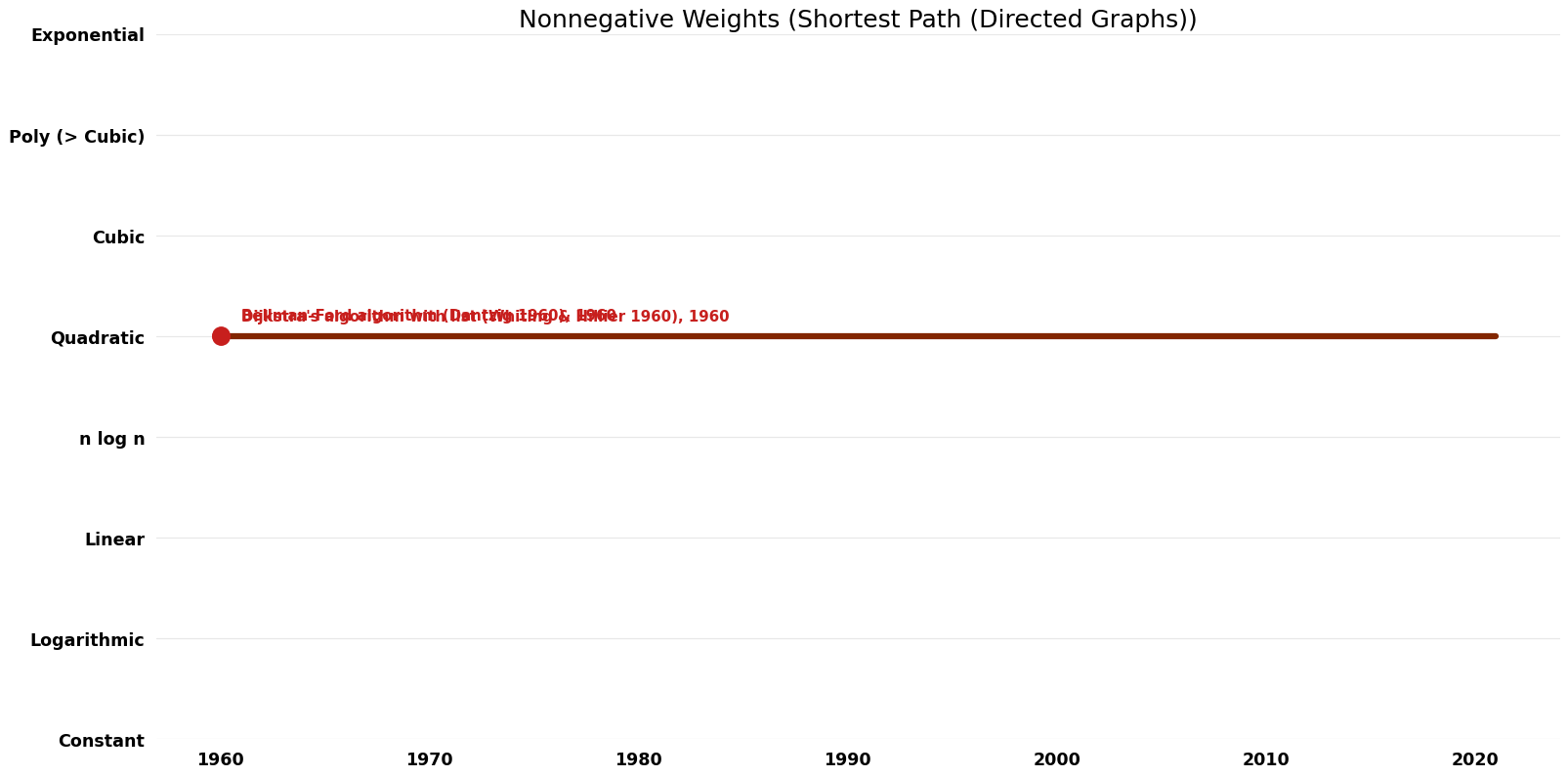
| [[Bellman–Ford algorithm (Dantzig 1960) (Nonnegative Weights Shortest Path (Directed Graphs))|Bellman–Ford algorithm (Dantzig )]] || 1960 || $O( | | [[Bellman–Ford algorithm (Dantzig 1960) (Nonnegative Weights Shortest Path (Directed Graphs))|Bellman–Ford algorithm (Dantzig )]] || 1960 || $O(V^{2} \log V)$ || $O(E)$ (total) || Exact || Deterministic || [https://www.jstor.org/stable/pdf/2627005.pdf Time] | ||
|- | |- | ||
| [[Dijkstra's algorithm with list (Whiting & Hillier 1960) (Nonnegative Weights Shortest Path (Directed Graphs))|Dijkstra's algorithm with list (Whiting & Hillier )]] || 1960 || $O( | | [[Dijkstra's algorithm with list (Whiting & Hillier 1960) (Nonnegative Weights Shortest Path (Directed Graphs))|Dijkstra's algorithm with list (Whiting & Hillier )]] || 1960 || $O(V^{2})$ || $O(V)$ || Exact || Deterministic || [https://www.jstor.org/stable/3007178?seq=1#page_scan_tab_contents Time] | ||
|- | |- | ||
| [[Dijkstra's algorithm with binary heap (Johnson 1977) (Nonnegative Weights Shortest Path (Directed Graphs))|Dijkstra's algorithm with binary heap (Johnson )]] || 1977 || $O((E + V) log V)$ || $O(V)$ | | [[Dijkstra's algorithm with binary heap (Johnson 1977) (Nonnegative Weights Shortest Path (Directed Graphs))|Dijkstra's algorithm with binary heap (Johnson )]] || 1977 || $O((E + V) \log V)$ || $O(V)$ || Exact || Deterministic || [https://dl.acm.org/citation.cfm?id=321993 Time] | ||
|- | |- | ||
| [[Dijkstra's algorithm with Fibonacci heap (Fredman & Tarjan 1984; Fredman & Tarjan 1987) (Nonnegative Weights Shortest Path (Directed Graphs))|Dijkstra's algorithm with Fibonacci heap (Fredman & Tarjan ; Fredman & Tarjan 1987)]] || 1984 || $O(E + V log V)$ || $O(V)$ | | [[Dijkstra's algorithm with Fibonacci heap (Fredman & Tarjan 1984; Fredman & Tarjan 1987) (Nonnegative Weights Shortest Path (Directed Graphs))|Dijkstra's algorithm with Fibonacci heap (Fredman & Tarjan ; Fredman & Tarjan 1987)]] || 1984 || $O(E + V \log V)$ || $O(V)$ || Exact || Deterministic || [https://www.cs.princeton.edu/courses/archive/fall03/cs528/handouts/fibonacci%20heaps.pdf Time] | ||
|- | |- | ||
| [[Gabow's algorithm (Nonnegative Weights Shortest Path (Directed Graphs))|Gabow's algorithm]] || 1983 || $O(E | | [[Gabow's algorithm (Nonnegative Weights Shortest Path (Directed Graphs))|Gabow's algorithm]] || 1983 || $O(E \log L/\log({2}+(E/V)))$ || $O(V+E)$? || Exact || Deterministic || [https://ieeexplore.ieee.org/document/4568085 Time] | ||
|- | |- | ||
|} | |} | ||
| Line 43: | Line 43: | ||
[[File:Shortest Path (Directed Graphs) - Nonnegative Weights - Time.png|1000px]] | [[File:Shortest Path (Directed Graphs) - Nonnegative Weights - Time.png|1000px]] | ||
== References/Citation == | == References/Citation == | ||
https://www.cs.princeton.edu/courses/archive/fall03/cs528/handouts/fibonacci%20heaps.pdf | https://www.cs.princeton.edu/courses/archive/fall03/cs528/handouts/fibonacci%20heaps.pdf | ||
Latest revision as of 10:06, 28 April 2023
Description
The shortest path problem is the problem of finding a path between two vertices (or nodes) in a graph such that the sum of the weights of its constituent edges is minimized. Here, the weights are restricted to be nonnegative.
Related Problems
Generalizations: general weights
Subproblem: Nonnegative Integer Weights
Related: General Weights, Second Shortest Simple Path, st-Shortest Path, 1-sensitive (3/2)-approximate ss-shortest paths, 2-sensitive (7/5)-approximate st-shortest paths, 1-sensitive decremental st-shortest paths, 2-sensitive decremental st-shortest paths, Replacement Paths Problem
Parameters
$V$: number of vertices
$E$: number of edges
$L$: maximum absolute value of edge cost
Table of Algorithms
| Name | Year | Time | Space | Approximation Factor | Model | Reference |
|---|---|---|---|---|---|---|
| Bellman–Ford algorithm (Dantzig ) | 1960 | $O(V^{2} \log V)$ | $O(E)$ (total) | Exact | Deterministic | Time |
| Dijkstra's algorithm with list (Whiting & Hillier ) | 1960 | $O(V^{2})$ | $O(V)$ | Exact | Deterministic | Time |
| Dijkstra's algorithm with binary heap (Johnson ) | 1977 | $O((E + V) \log V)$ | $O(V)$ | Exact | Deterministic | Time |
| Dijkstra's algorithm with Fibonacci heap (Fredman & Tarjan ; Fredman & Tarjan 1987) | 1984 | $O(E + V \log V)$ | $O(V)$ | Exact | Deterministic | Time |
| Gabow's algorithm | 1983 | $O(E \log L/\log({2}+(E/V)))$ | $O(V+E)$? | Exact | Deterministic | Time |
Time Complexity Graph
References/Citation
https://www.cs.princeton.edu/courses/archive/fall03/cs528/handouts/fibonacci%20heaps.pdf