Strongly Connected Components: Difference between revisions
Jump to navigation
Jump to search
(Created page with "== Problem Description== Connectivity in an undirected graph means that every vertex can reach every other vertex via any path. If the graph is not connected the graph can be broken down into Connected Components. Strong Connectivity applies only to directed graphs. A directed graph is strongly connected if there is a directed path from any vertex to every other vertex. This is same as connectivity in an undirected graph, the only difference being strong connectivity ap...") |
No edit summary |
||
| (6 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
== | {{DISPLAYTITLE:Strongly Connected Components (Strongly Connected Components)}} | ||
== Description == | |||
The strongly connected components or diconnected components of an arbitrary directed graph form a partition into subgraphs that are themselves strongly connected. | |||
== | == Related Problems == | ||
Related: [[Transitive Closure]], [[Maximum Strongly Connected Component]], [[Strong Connectivity (dynamic)]], [[2 Strong Components (dynamic)]], [[Connected Subgraph]] | |||
[[ | |||
== | == Parameters == | ||
$V$: number of vertices | |||
$E$: number of edges | |||
== Table of Algorithms == | |||
Currently no algorithms in our database for the given problem. | |||
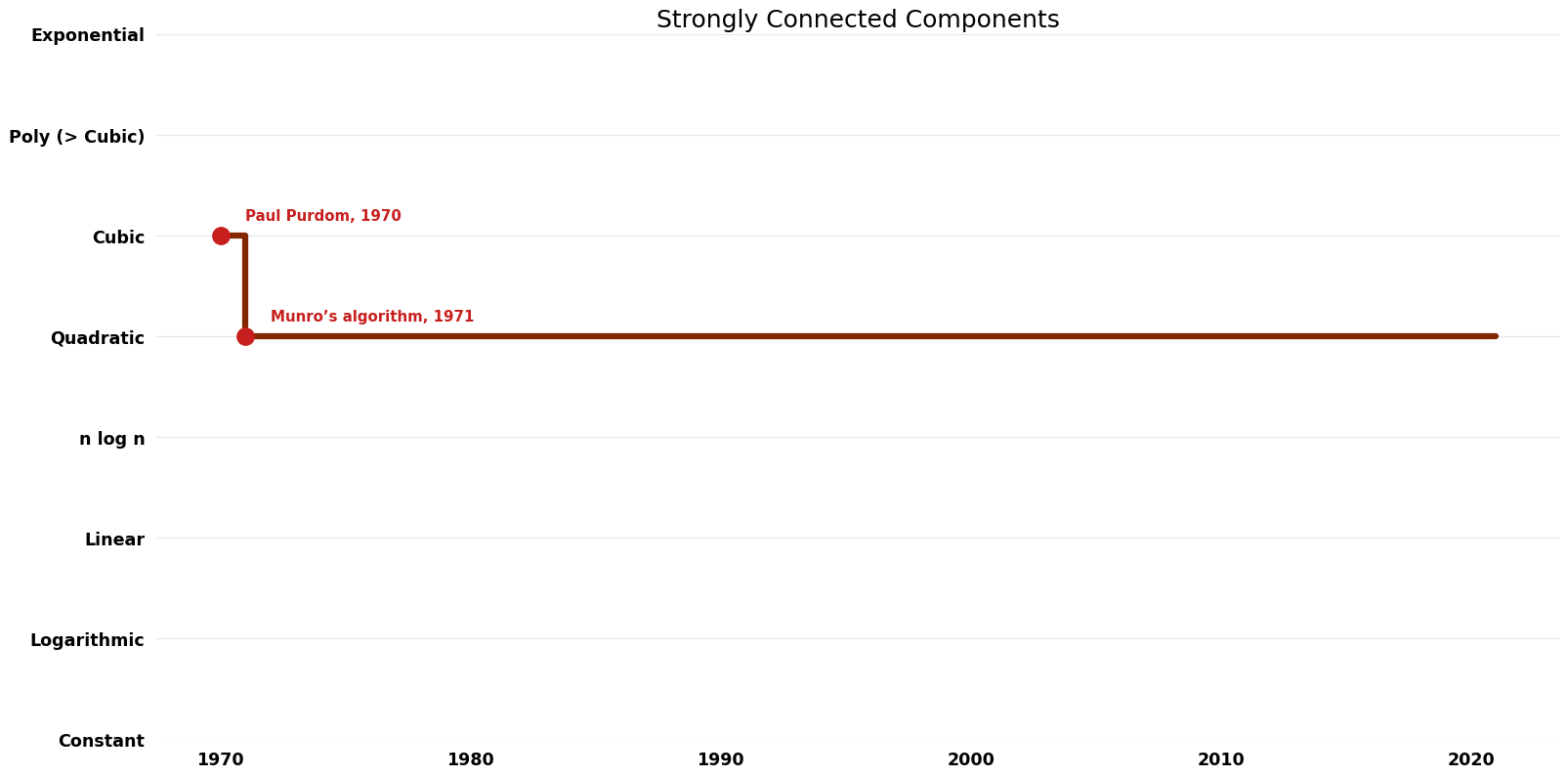
== Time Complexity Graph == | |||
[ | [[File:Strongly Connected Components - Time.png|1000px]] | ||
[ | |||
Latest revision as of 10:06, 28 April 2023
Description
The strongly connected components or diconnected components of an arbitrary directed graph form a partition into subgraphs that are themselves strongly connected.
Related Problems
Related: Transitive Closure, Maximum Strongly Connected Component, Strong Connectivity (dynamic), 2 Strong Components (dynamic), Connected Subgraph
Parameters
$V$: number of vertices
$E$: number of edges
Table of Algorithms
Currently no algorithms in our database for the given problem.