Matrix Multiplication

Description

Matrix Multiplication or Matrix Product is a binary operation that produces a matrix from two matrices with entries in a field; or; more generally; in a ring or even a semiring.

Related Problems

Subproblem: Boolean Matrix Multiplication, Matrix Product Verification

Related: Boolean Matrix Multiplication (Combinatorial), Matrix Product Verification, Distance Product, $(\min, \leq)$ Product

Parameters

$n$: dimension of square matrix

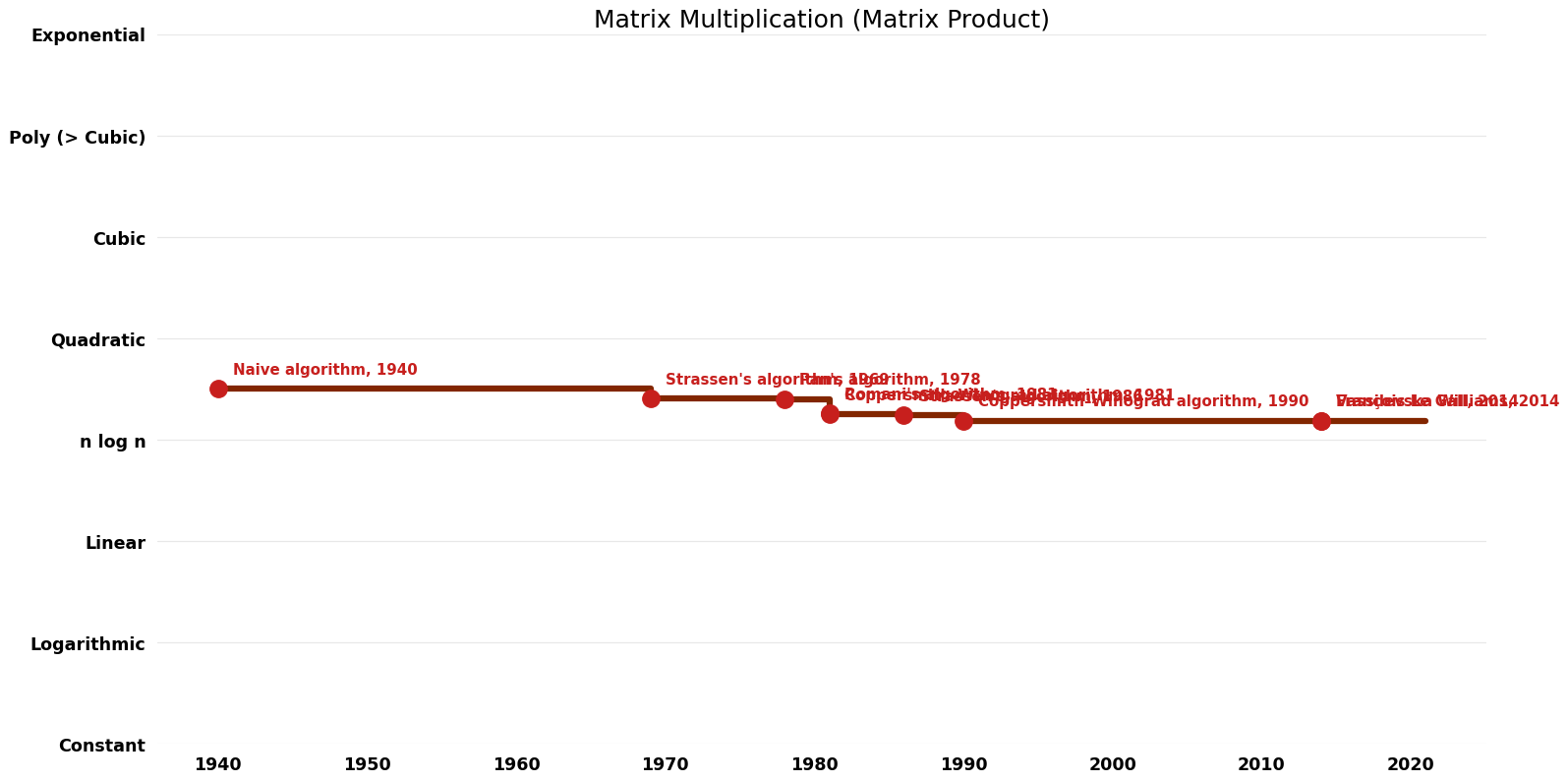
Table of Algorithms

Name	Year	Time	Space	Approximation Factor	Model	Reference
Naive algorithm	1940	$O(n^{3})$	$O({1})$ auxiliary	Exact	Deterministic
Strassen's algorithm	1969	$O(n^{(log7/log2)}) ~ O(n^{2.{80}7})$	$O(n^{2})$	Exact	Deterministic	Time & Space
Pan's algorithm	1978	$O(n^{(log({143640})/log({70}))}) ~ O(n^{2.{79}5})$	$O(n^{2})$	Exact	Deterministic	Time
Romani's algorithm	1981	$O(n^{2.{5166}5})$	$O(n^{2})$	Exact	Deterministic	Time
Coppersmith–Winograd algorithm	1981	$O(n^{2.{49554}8})$	$O(n^{2})$	Exact	Deterministic	Time
Strassen's algorithm	1986	$O(n^{(log54/log5)}) ~ O(n^{({2.4785})})$	$O(n^{2})$	Exact	Deterministic	Time
Coppersmith–Winograd algorithm	1990	$O(n^{2.{375}5})$	$O(n^{2})$	Exact	Deterministic	Time
Vassilevska Williams	2014	$O(n^{2.{37287}3})$	$O(n^{2})$	Exact	Deterministic	Time
François Le Gall	2014	$O(n^{2.{372863}9})$	$O(n^{2})$	Exact	Deterministic	Time
Bini's algorithm	1979	$O(n^{2.{779}9})$	$O(n^{2})$	$O(n logn)$ error	Deterministic	Time
Schonhage's algorithm	1980	$O(n^{({3}*\log {52}/l \og {110})}) ~ O(n^{2.{521}8})$	$O(n^{2})$	?	Deterministic	Time
Output-Sensitive Quantum BMM	2018	O*( \min \{n^{1/3} L^{17/{3}0}, n^{1.5} L^{1/4}\})		Exact	Quantum	Time
	2018	$O(n^{3} / log^{2.25} n)$		Exact	Deterministic	Time
O'Neil	1973	$O(n^{3})$		Exact	Deterministic	Time
Method of Four Russians	1970	$O(n^{3}/(log n)$^{2})		Exact	Deterministic	Time
Bansal, Williams	2009	$O(n^{3} * (log log n)$^{2} / log^{2.25} n)		Exact	Randomized	Time
Bansal, Williams	2009	$O(n^{3} * (log log n)$^{2} / (w * (log n)^{7}/{6}))		Exact	Randomized	Time
Chan	2015	$O(n^{3} * (log log n)$^{3} / log^{3} n)		Exact	Deterministic	Time
Chan	2015	$O(n^{3} * (log w)$^{3} / (w * log^{2} n))		Exact	Deterministic	Time
Yu	2015	$O(n^{3}*poly(log log n)$/log^{4} n)		Exact	Deterministic	Time

Time Complexity Graph

References/Citation

https://arxiv.org/pdf/2010.05846.pdf