Kth Order Statistic: Difference between revisions
Jump to navigation
Jump to search
No edit summary |
No edit summary |
||
| (2 intermediate revisions by the same user not shown) | |||
| Line 6: | Line 6: | ||
== Parameters == | == Parameters == | ||
n: size of list | $n$: size of list | ||
== Table of Algorithms == | == Table of Algorithms == | ||
| Line 16: | Line 16: | ||
|- | |- | ||
| [[Naive Selection (kth Order Statistic kth Order Statistic)|Naive Selection]] || 1940 || $O( | | [[Naive Selection (kth Order Statistic kth Order Statistic)|Naive Selection]] || 1940 || $O(n \log n)$ || $O({1})$ (in-situ) || Exact || Deterministic || | ||
|- | |- | ||
| [[Hoare's Selection Algorithm (QuickSelect) (kth Order Statistic kth Order Statistic)|Hoare's Selection Algorithm (QuickSelect)]] || 1961 || $O(n)$ || $O({1})$ (in-situ) || Exact || Deterministic || [https://dl.acm.org/citation.cfm?doid=366622.366647 Time] | | [[Hoare's Selection Algorithm (QuickSelect) (kth Order Statistic kth Order Statistic)|Hoare's Selection Algorithm (QuickSelect)]] || 1961 || $O(n^{2})$ || $O({1})$ (in-situ) || Exact || Deterministic || [https://dl.acm.org/citation.cfm?doid=366622.366647 Time] | ||
|- | |- | ||
| [[Hashing (kth Order Statistic kth Order Statistic)|Hashing]] || 1940 || $O(n)$ || $O(n)$ || Exact || Deterministic || | | [[Hashing (kth Order Statistic kth Order Statistic)|Hashing]] || 1940 || $O(n)$ || $O(n)$ || Exact || Deterministic || | ||
| Line 27: | Line 27: | ||
[[File:kth Order Statistic - Time.png|1000px]] | [[File:kth Order Statistic - Time.png|1000px]] | ||
== References/Citation == | == References/Citation == | ||
https://11011110.github.io/blog/2007/10/09/blum-style-analysis-of.html | https://11011110.github.io/blog/2007/10/09/blum-style-analysis-of.html | ||
Latest revision as of 10:04, 28 April 2023
Description
An algorithm seeks to find the $k^{th}$ order statistic of a statistical sample, or the $k^{th}$-smallest value in a list or array.
Parameters
$n$: size of list
Table of Algorithms
| Name | Year | Time | Space | Approximation Factor | Model | Reference |
|---|---|---|---|---|---|---|
| Naive Selection | 1940 | $O(n \log n)$ | $O({1})$ (in-situ) | Exact | Deterministic | |
| Hoare's Selection Algorithm (QuickSelect) | 1961 | $O(n^{2})$ | $O({1})$ (in-situ) | Exact | Deterministic | Time |
| Hashing | 1940 | $O(n)$ | $O(n)$ | Exact | Deterministic |
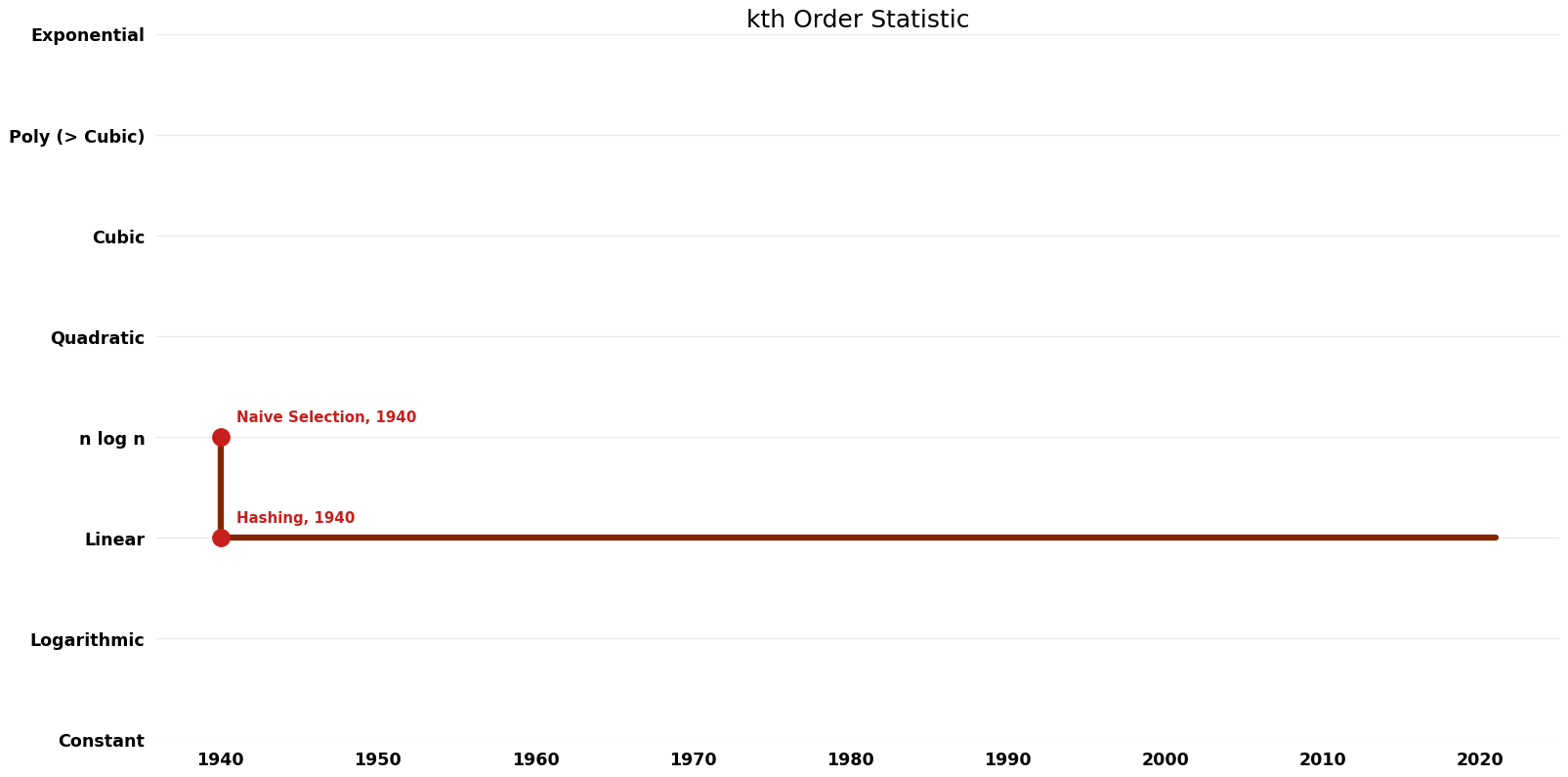
Time Complexity Graph
References/Citation
https://11011110.github.io/blog/2007/10/09/blum-style-analysis-of.html