Median String Problem with Unbounded Alphabets: Difference between revisions
Jump to navigation
Jump to search
No edit summary |
No edit summary |
||
| Line 10: | Line 10: | ||
== Parameters == | == Parameters == | ||
n: number of strings | $n$: number of strings | ||
== Table of Algorithms == | == Table of Algorithms == | ||
| Line 20: | Line 20: | ||
|- | |- | ||
| [[Naive Solution (Median String Problem with Unbounded Alphabets Median String Problem)|Naive Solution]] || 1965 || {2}^$O(n)$ || $O(n)$ | | [[Naive Solution (Median String Problem with Unbounded Alphabets Median String Problem)|Naive Solution]] || 1965 || {2}^$O(n)$ || $O(n)$ || Exact || Deterministic || | ||
|- | |- | ||
|} | |} | ||
Revision as of 09:25, 10 April 2023
Description
Given an unbounded alphabet $\Sigma$, a set $W$ of strings over $\Sigma$, and the Levenshtein distance between strings, find a string over $\Sigma$ that minimizes the sum of distances to the strings of $W$.
Related Problems
Related: Median String Problem with Bounded Alphabets, Median String Problem with Binary Alphabets
Parameters
$n$: number of strings
Table of Algorithms
| Name | Year | Time | Space | Approximation Factor | Model | Reference |
|---|---|---|---|---|---|---|
| Naive Solution | 1965 | {2}^$O(n)$ | $O(n)$ | Exact | Deterministic |
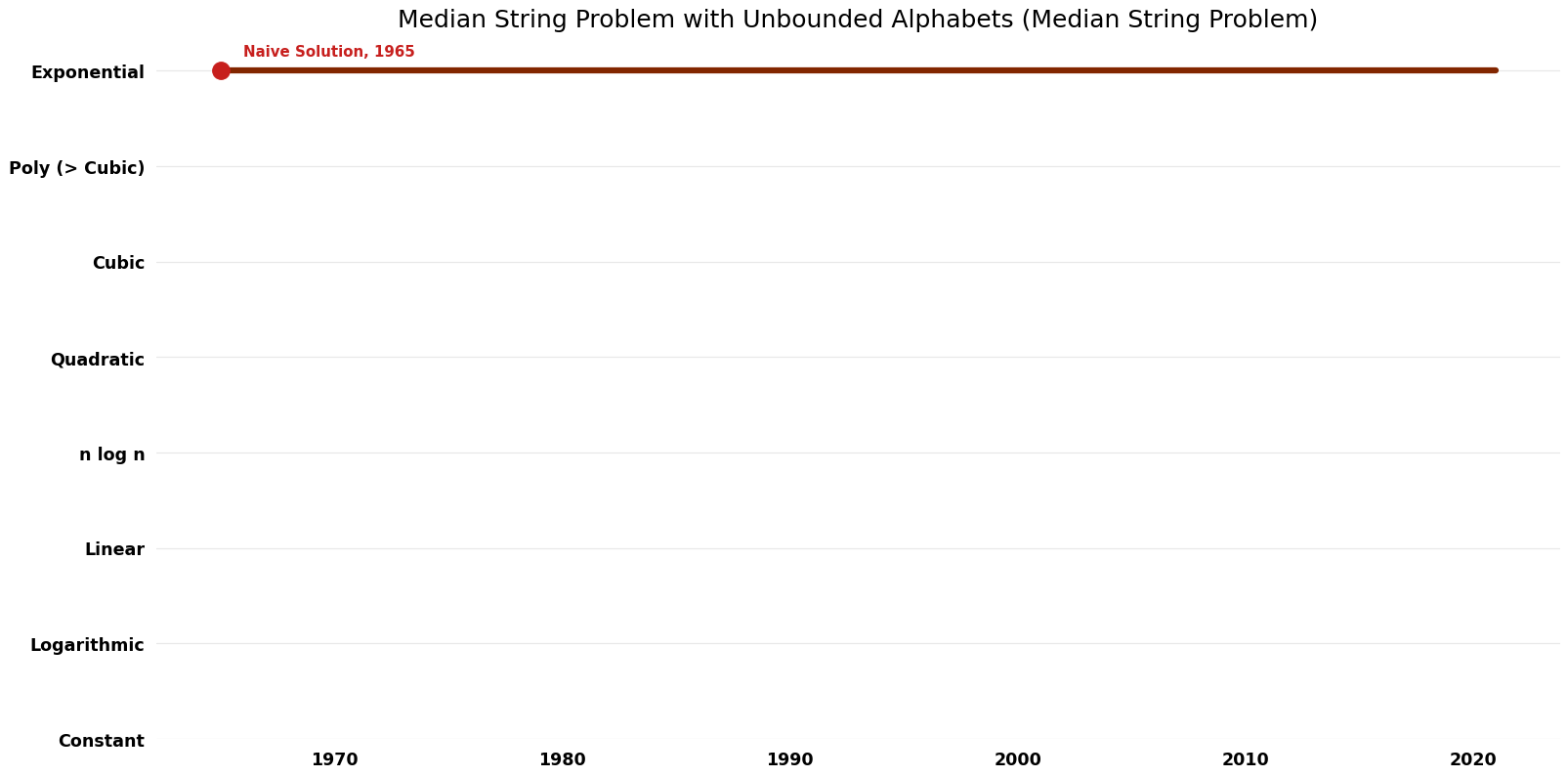
Time Complexity Graph
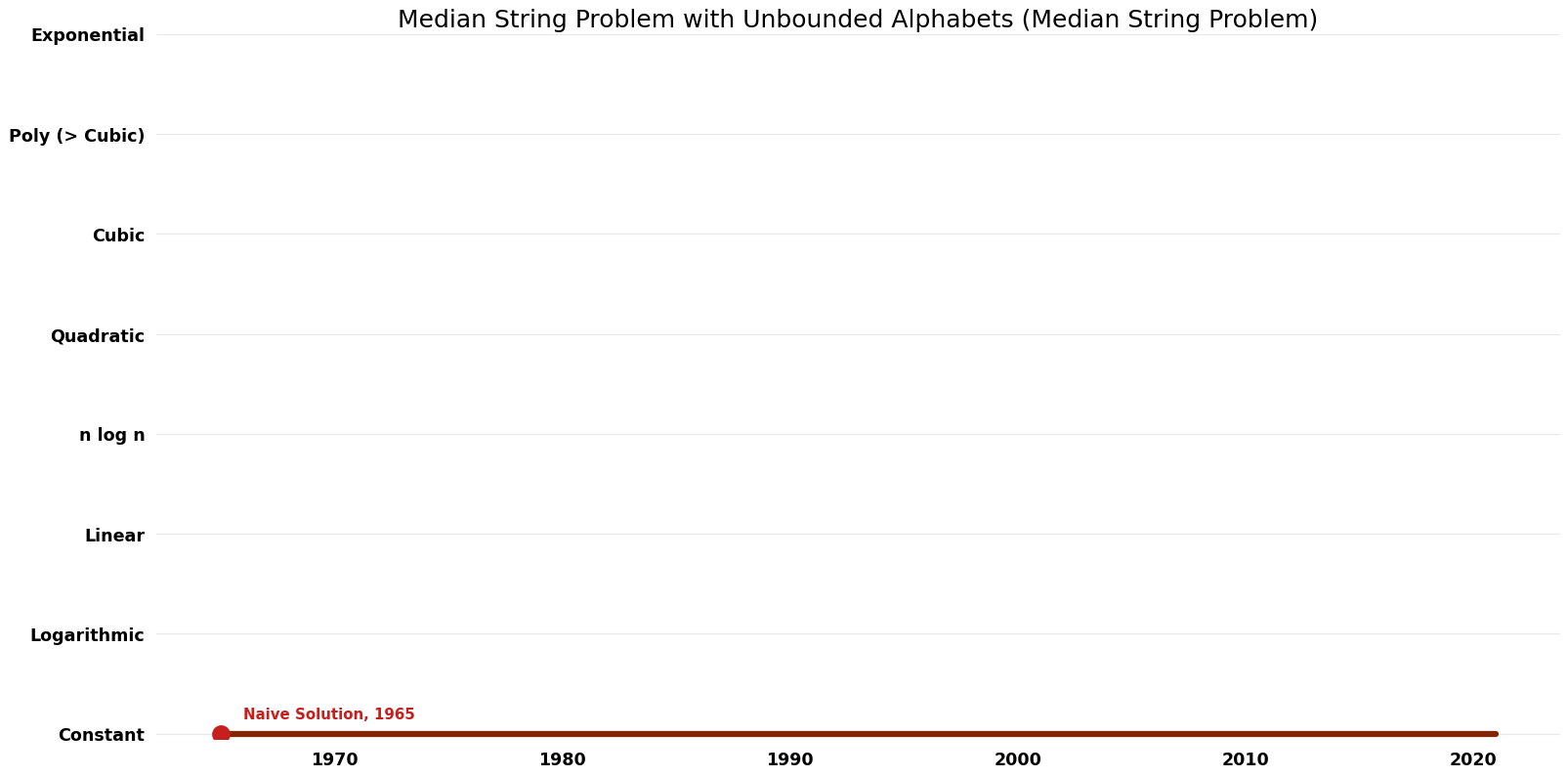
Space Complexity Graph
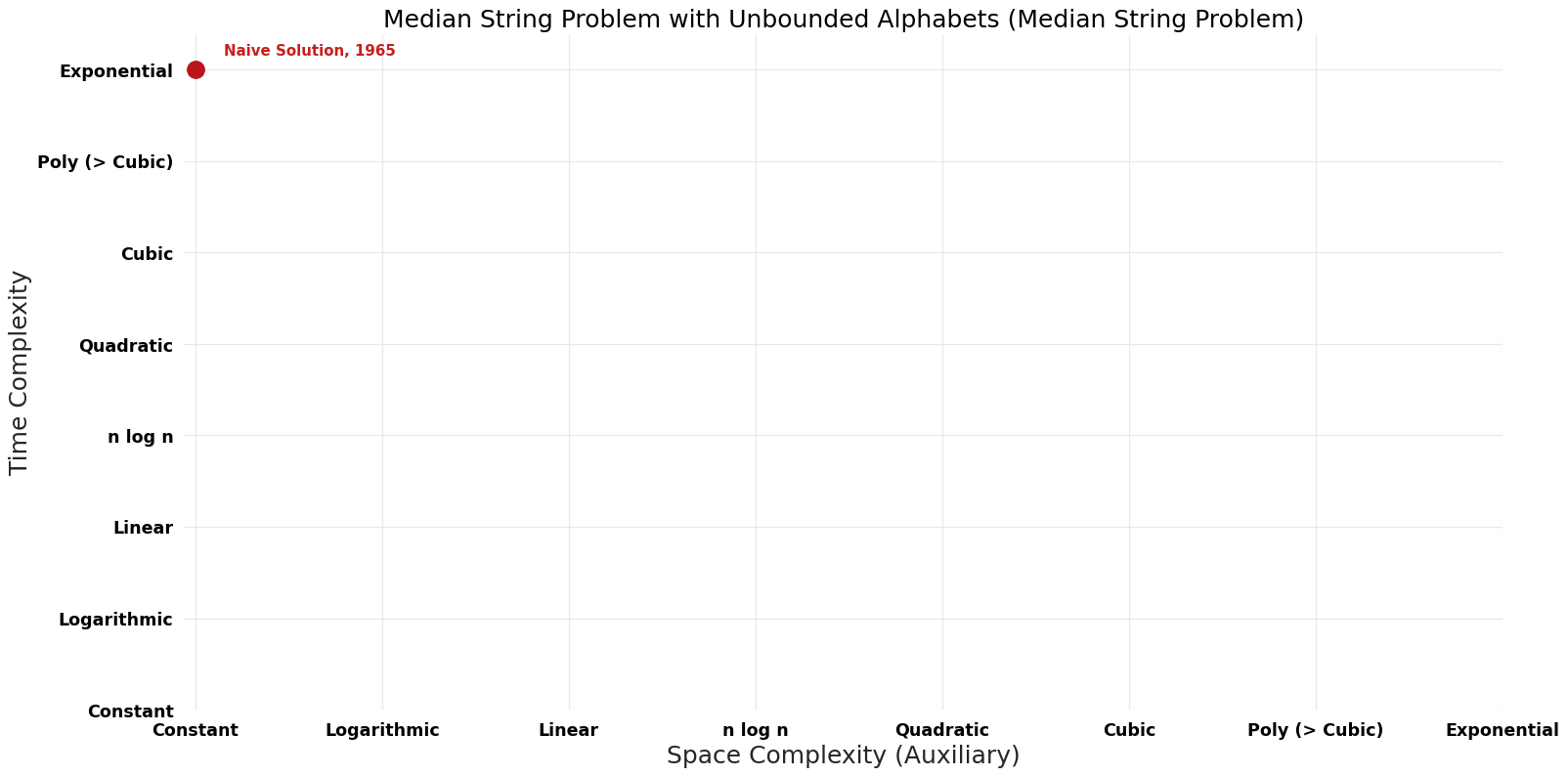
Time-Space Tradeoff
References/Citation
https://link.springer.com/content/pdf/10.1007/3-540-44888-8_23.pdf