Maximum Cut: Difference between revisions
Jump to navigation
Jump to search
(Created page with "{{DISPLAYTITLE:Maximum Cut (Maximum Cut)}} == Description == Given a graph $G=(V, E)$ with edge weights $c_e > 0$ for all $e\in E$, find a cut $\delta(W)$ such that $c(\delta(W)):=\Sigma_{e\in \dela(W)} c_e$ is as large as possible. == Parameters == <pre>n: number of vertices m: number of edges</pre> == Table of Algorithms == {| class="wikitable sortable" style="text-align:center;" width="100%" ! Name !! Year !! Time !! Space !! Approximation Factor !! Model !!...") |
No edit summary |
||
| (2 intermediate revisions by the same user not shown) | |||
| Line 6: | Line 6: | ||
== Parameters == | == Parameters == | ||
$n$: number of vertices | |||
m: number of edges | |||
$m$: number of edges | |||
== Table of Algorithms == | == Table of Algorithms == | ||
| Line 17: | Line 18: | ||
|- | |- | ||
| [[Hadlock (Maximum Cut Maximum Cut)|Hadlock]] || 1975 || $O({2}^ | | [[Hadlock (Maximum Cut Maximum Cut)|Hadlock]] || 1975 || $O({2}^n)$ || || Exact || Deterministic || | ||
|- | |||
| [[Motwani & Raghavan (Maximum Cut, Approximate Maximum Cut)|Motwani & Raghavan]] || 1995 || $O(n)$? || $O(n)$ || 0.5 || Randomized || [https://rajsain.files.wordpress.com/2013/11/randomized-algorithms-motwani-and-raghavan.pdf Time] | |||
|- | |||
| [[Mitzenmacher & Upfal (Maximum Cut, Approximate Maximum Cut)|Mitzenmacher & Upfal]] || 2005 || $O(mn)$? || $O(n)$ || 0.5 || Deterministic || [http://lib.ysu.am/open_books/413311.pdf Time] | |||
|- | |||
| [[Khuller; Raghavachari & Young, "Greedy Methods" (Maximum Cut, Approximate Maximum Cut)|Khuller; Raghavachari & Young, "Greedy Methods"]] || 2007 || $O(n^{2})$? || $O(n)$ || 0.5 || Deterministic || [https://doc.lagout.org/science/0_Computer%20Science/2_Algorithms/Handbook%20of%20Approximation%20Algorithms%20and%20Metaheuristics%20%5BGonzalez%202007-01-05%5D.pdf Time] | |||
|- | |||
| [[Ausiello et al. (Maximum Cut, Approximate Maximum Cut)|Ausiello et al.]] || 2003 || $O(n^{3} \log m)$ || $O(n^{2})$? || ~0.878; assuming this is the goemans-williamson algorithm || Deterministic || [https://link.springer.com/content/pdf/10.1007/978-3-642-58412-1.pdf?pdf=button Time] | |||
|- | |||
| [[Dunning; Gupta & Silberholz (Maximum Cut, Approximate Maximum Cut)|Dunning; Gupta & Silberholz]] || 2018 || $O(mn)$ || || Exact || Deterministic || [https://pubsonline.informs.org/doi/epdf/10.1287/ijoc.2017.0798 Time] | |||
|- | |- | ||
|} | |} | ||
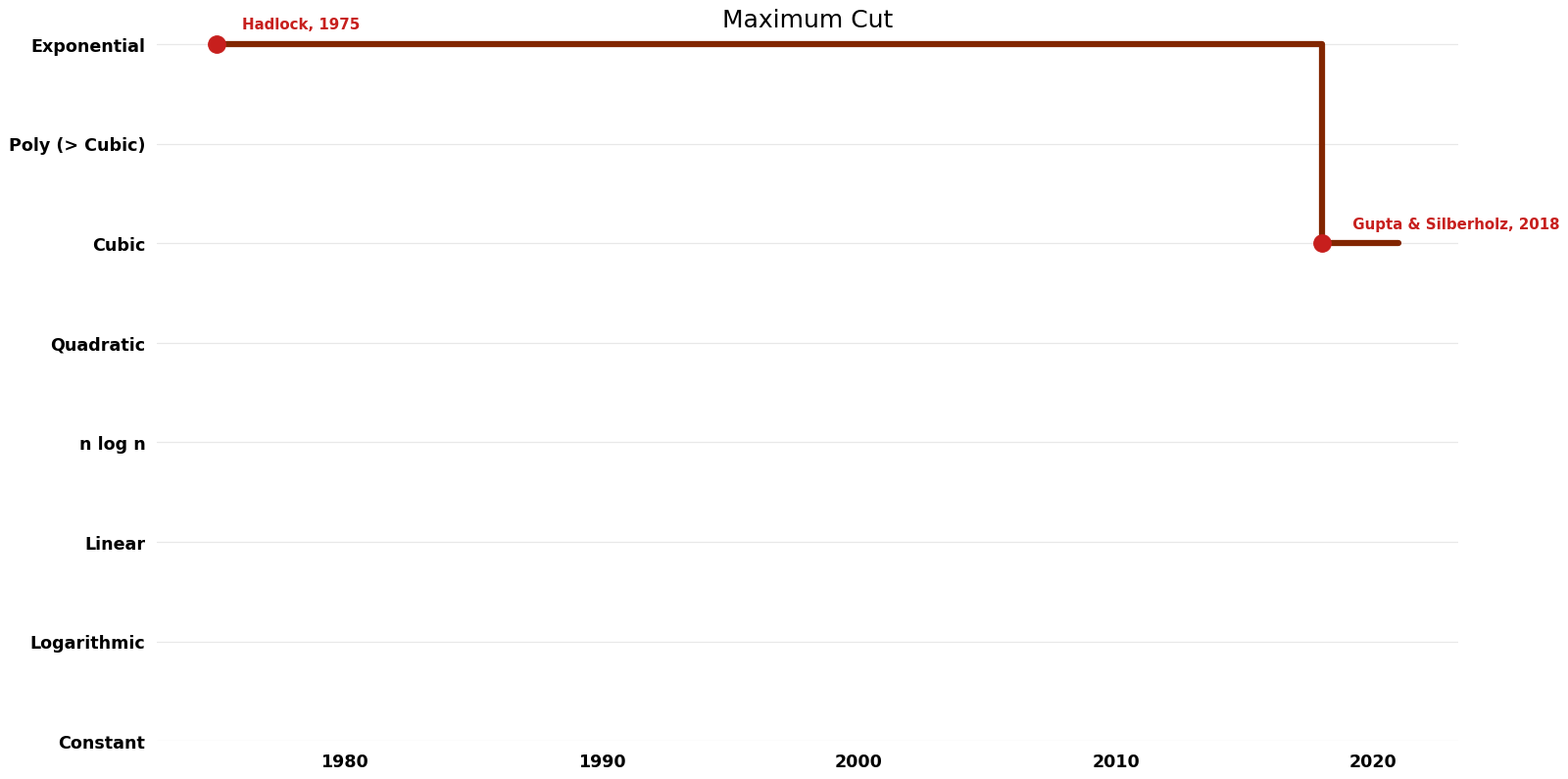
== Time Complexity | == Time Complexity Graph == | ||
[[File:Maximum Cut - Time.png|1000px]] | [[File:Maximum Cut - Time.png|1000px]] | ||
Latest revision as of 09:24, 10 April 2023
Description
Given a graph $G=(V, E)$ with edge weights $c_e > 0$ for all $e\in E$, find a cut $\delta(W)$ such that $c(\delta(W)):=\Sigma_{e\in \dela(W)} c_e$ is as large as possible.
Parameters
$n$: number of vertices
$m$: number of edges
Table of Algorithms
| Name | Year | Time | Space | Approximation Factor | Model | Reference |
|---|---|---|---|---|---|---|
| Hadlock | 1975 | $O({2}^n)$ | Exact | Deterministic | ||
| Motwani & Raghavan | 1995 | $O(n)$? | $O(n)$ | 0.5 | Randomized | Time |
| Mitzenmacher & Upfal | 2005 | $O(mn)$? | $O(n)$ | 0.5 | Deterministic | Time |
| Khuller; Raghavachari & Young, "Greedy Methods" | 2007 | $O(n^{2})$? | $O(n)$ | 0.5 | Deterministic | Time |
| Ausiello et al. | 2003 | $O(n^{3} \log m)$ | $O(n^{2})$? | ~0.878; assuming this is the goemans-williamson algorithm | Deterministic | Time |
| Dunning; Gupta & Silberholz | 2018 | $O(mn)$ | Exact | Deterministic | Time |