CFG Parsing: Difference between revisions
Jump to navigation
Jump to search
No edit summary |
No edit summary |
||
| Line 10: | Line 10: | ||
== Parameters == | == Parameters == | ||
n: length of the given string | $n$: length of the given string | ||
$|G|$: size of the grammar | |||
== Table of Algorithms == | == Table of Algorithms == | ||
| Line 22: | Line 24: | ||
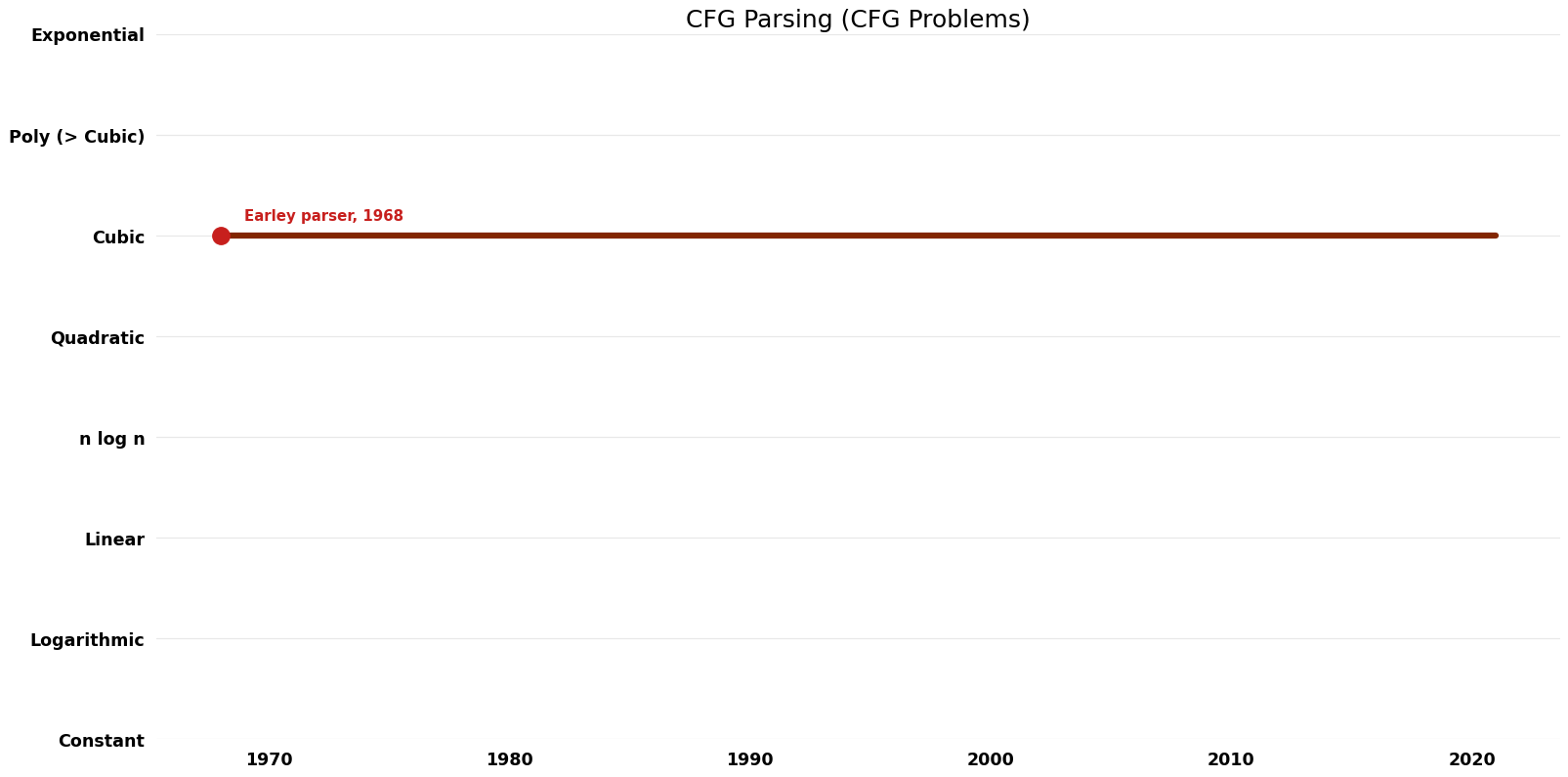
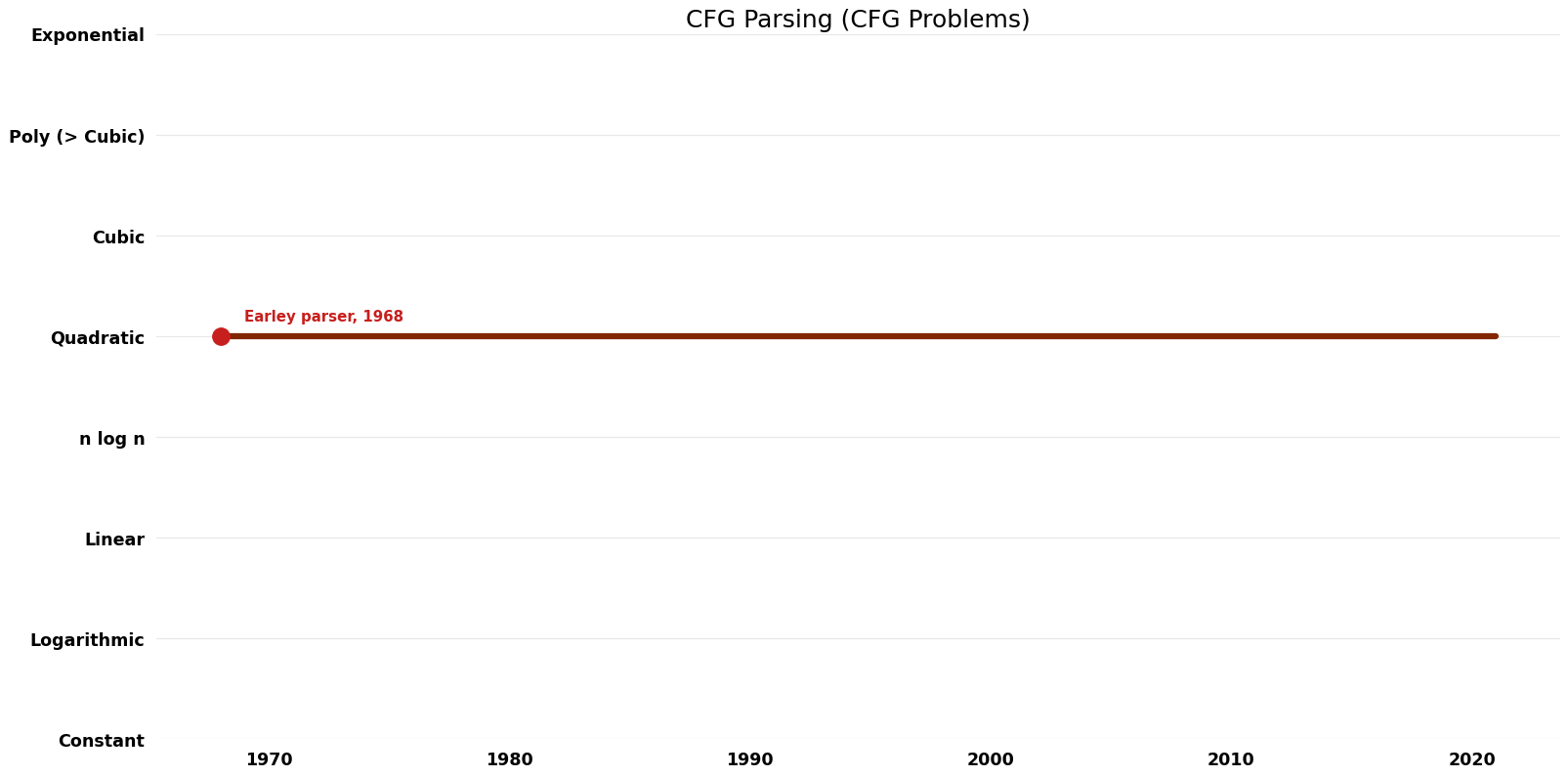
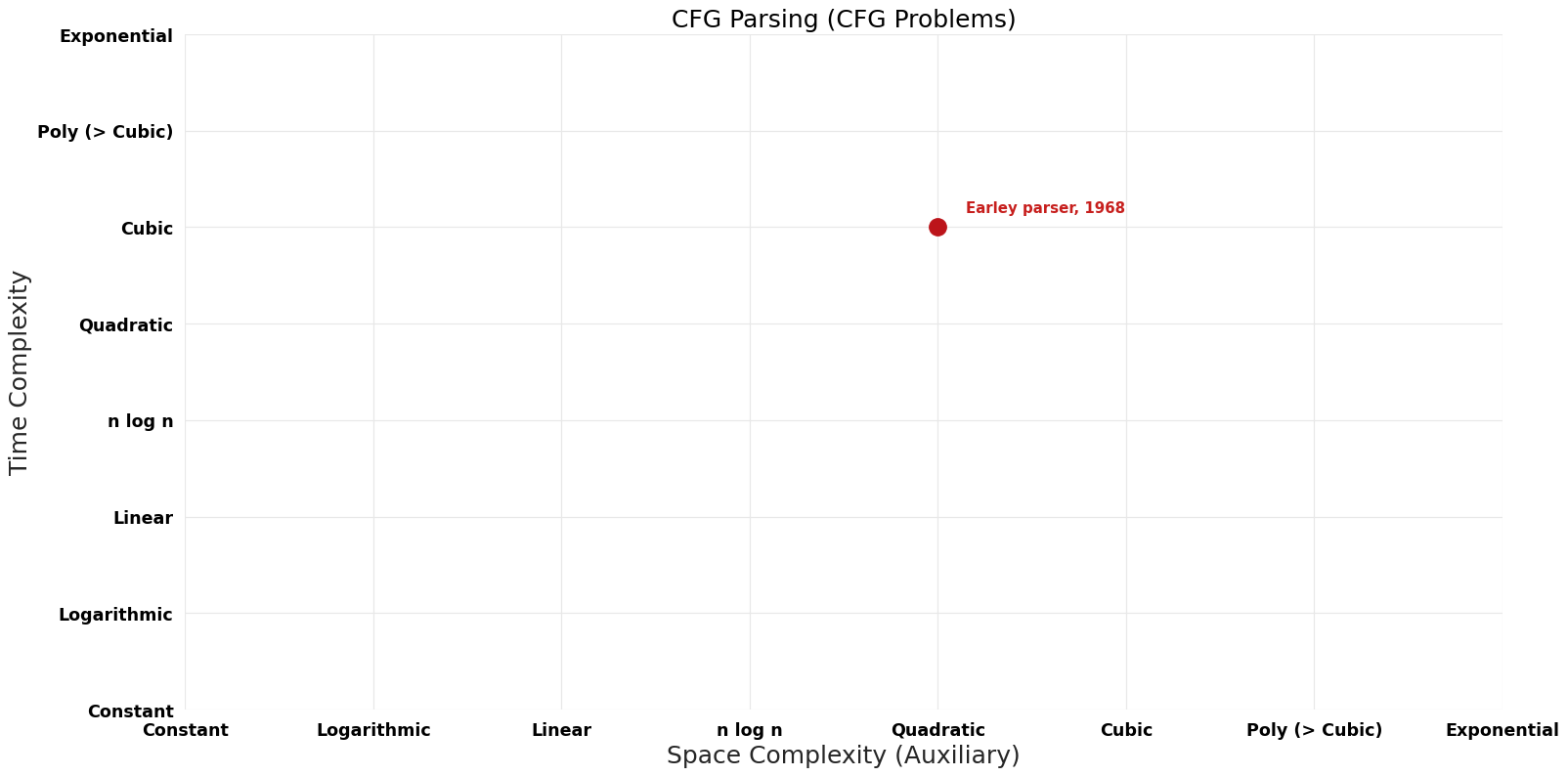
| [[Earley parser (CFG Parsing CFG Problems)|Earley parser]] || 1968 || $O(n^{3})$ || $O(n^{2})$ || Exact || Deterministic || [https://web.archive.org/web/20040708052627/http://www-2.cs.cmu.edu/afs/cs.cmu.edu/project/cmt-55/lti/Courses/711/Class-notes/p94-earley.pdf Time & Space] | | [[Earley parser (CFG Parsing CFG Problems)|Earley parser]] || 1968 || $O(n^{3})$ || $O(n^{2})$ || Exact || Deterministic || [https://web.archive.org/web/20040708052627/http://www-2.cs.cmu.edu/afs/cs.cmu.edu/project/cmt-55/lti/Courses/711/Class-notes/p94-earley.pdf Time & Space] | ||
|- | |- | ||
| [[GLR parser (CFG Parsing CFG Problems)|GLR parser]] || 1974 || $O(n^{3})$ || $O(n^{3})$ || Exact || Deterministic || [https://link.springer.com/chapter/10.1007%2F978-3-662-21545-6_18 Time | | [[GLR parser (CFG Parsing CFG Problems)|GLR parser]] || 1974 || $O(n^{3})$ || $O(n^{3})$ || Exact || Deterministic || [https://link.springer.com/chapter/10.1007%2F978-3-662-21545-6_18 Time & Space] | ||
|- | |- | ||
|} | |} | ||
Revision as of 09:22, 10 April 2023
Description
Given a grammar $G$ and a string $s$, find the parse structure, or analysis, assigned to the string $s$ by the grammar $G$.
Related Problems
Related: CFG Recognition
Parameters
$n$: length of the given string
$|G|$: size of the grammar
Table of Algorithms
| Name | Year | Time | Space | Approximation Factor | Model | Reference |
|---|---|---|---|---|---|---|
| Earley parser | 1968 | $O(n^{3})$ | $O(n^{2})$ | Exact | Deterministic | Time & Space |
| GLR parser | 1974 | $O(n^{3})$ | $O(n^{3})$ | Exact | Deterministic | Time & Space |
Time Complexity Graph
Space Complexity Graph
Time-Space Tradeoff
Reductions TO Problem
| Problem | Implication | Year | Citation | Reduction |
|---|---|---|---|---|
| BMM | if: to-time: $O(n^{3-\epsilon})$ for some $\epsilon > {0}$ where $n \times n$ matrix then: from-time: $O(gn^{3-\epsilon})$ where $g$ is the size of the CFG |
1975 | https://www.sciencedirect.com/science/article/pii/S0022000075800468 | link |
Reductions FROM Problem
| Problem | Implication | Year | Citation | Reduction |
|---|---|---|---|---|
| BMM | if: to-time: $O(gn^{3-\epsilon})$ for some $\epsilon > {0}$ where $g$ is the size of the CFG and $n$ is the size of the string then: from-time: $O(n^{3-\epsilon/3})$ where $n \times n$ matrix |
2002 | https://arxiv.org/abs/cs/0112018 | link |
References/Citation
https://link.springer.com/chapter/10.1007%2F978-3-662-21545-6_18