Enumerating Maximal Cliques, arbitrary graph: Difference between revisions
Jump to navigation
Jump to search
No edit summary |
No edit summary |
||
| Line 10: | Line 10: | ||
== Parameters == | == Parameters == | ||
n: number of vertices | $n$: number of vertices | ||
m: number of edges | $m$: number of edges | ||
== Table of Algorithms == | == Table of Algorithms == | ||
| Line 22: | Line 22: | ||
|- | |- | ||
| [[Bron–Kerbosch algorithm (Enumerating Maximal Cliques, arbitrary graph Clique Problems)|Bron–Kerbosch algorithm]] || 1973 || $O({3}^{(n/{3})})$ || $O(n^{2})$ | | [[Bron–Kerbosch algorithm (Enumerating Maximal Cliques, arbitrary graph Clique Problems)|Bron–Kerbosch algorithm]] || 1973 || $O({3}^{(n/{3})})$ || $O(n^{2})$? || Exact || Deterministic || [https://dl.acm.org/doi/10.1145/362342.362367 Time] | ||
|- | |- | ||
| [[Akkoyunlu; E. A. (Enumerating Maximal Cliques, arbitrary graph Clique Problems)|Akkoyunlu; E. A. ]] || 1973 || $O({3}^{(n/{3})$}) || $O(n^{2})$ | | [[Akkoyunlu; E. A. (Enumerating Maximal Cliques, arbitrary graph Clique Problems)|Akkoyunlu; E. A. ]] || 1973 || $O({3}^{(n/{3})$}) || $O(n^{2})$? || Exact || Deterministic || [http://www.dcs.gla.ac.uk/~pat/jchoco/clique/enumeration/papers/SMJ000001%5B1%5D.pdf Time] | ||
|- | |- | ||
| [[Tomita; Tanaka & Takahashi (Enumerating Maximal Cliques, arbitrary graph Clique Problems)|Tomita; Tanaka & Takahashi]] || 2006 || $O({3}^{(n/{3})$}) || $O(n^{2})$ | | [[Tomita; Tanaka & Takahashi (Enumerating Maximal Cliques, arbitrary graph Clique Problems)|Tomita; Tanaka & Takahashi]] || 2006 || $O({3}^{(n/{3})$}) || $O(n^{2})$? || Exact || Deterministic || [https://snap.stanford.edu/class/cs224w-readings/tomita06cliques.pdf Time] | ||
|- | |- | ||
| [[Segundo; Artieda; Strash Parallel (Enumerating Maximal Cliques, arbitrary graph Clique Problems)|Segundo; Artieda; Strash Parallel]] || 2011 || $O({3}^{(n/{3})})$ total work? (previously this cell said $O(n^{4})$) || $O(n^{2})$ auxiliary?? || Exact || Parallel || [https://arxiv.org/pdf/1801.00202.pdf Time] | | [[Segundo; Artieda; Strash Parallel (Enumerating Maximal Cliques, arbitrary graph Clique Problems)|Segundo; Artieda; Strash Parallel]] || 2011 || $O({3}^{(n/{3})})$ total work? (previously this cell said $O(n^{4})$) || $O(n^{2})$ auxiliary?? || Exact || Parallel || [https://arxiv.org/pdf/1801.00202.pdf Time] | ||
|- | |- | ||
| [[David Eppstein, Maarten Löffler, Darren Strash (Enumerating Maximal Cliques, arbitrary graph Clique Problems)|David Eppstein, Maarten Löffler, Darren Strash]] || 2010 || $O(dn {3}^{(d/{3})})$ || $O(n^{2})$ | | [[David Eppstein, Maarten Löffler, Darren Strash (Enumerating Maximal Cliques, arbitrary graph Clique Problems)|David Eppstein, Maarten Löffler, Darren Strash]] || 2010 || $O(dn {3}^{(d/{3})})$ || $O(n^{2})$? || Exact || Deterministic || [https://arxiv.org/pdf/1006.5440.pdf Time] | ||
|- | |- | ||
| [[Chiba and Nishizeki (Enumerating Maximal Cliques, arbitrary graph Clique Problems)|Chiba and Nishizeki ]] || 1985 || $O(a(G)*m)$ per clique || $O(m)$ | | [[Chiba and Nishizeki (Enumerating Maximal Cliques, arbitrary graph Clique Problems)|Chiba and Nishizeki ]] || 1985 || $O(a(G)*m)$ per clique || $O(m)$ || Exact || Deterministic || [https://pdfs.semanticscholar.org/0d19/245a27bc65a87a8014d5b8a66fb514c8ff0b.pdf Time & Space] | ||
|- | |- | ||
| [[M. Chrobak and D. Eppstein (Enumerating Maximal Cliques, arbitrary graph Clique Problems)|M. Chrobak and D. Eppstein]] || 1989 || $O(n d^{2} {2}^d)$ || $O(n)$ | | [[M. Chrobak and D. Eppstein (Enumerating Maximal Cliques, arbitrary graph Clique Problems)|M. Chrobak and D. Eppstein]] || 1989 || $O(n d^{2} {2}^d)$ || $O(n)$? || Exact || Deterministic || [https://www.ics.uci.edu/~eppstein/pubs/ChrEpp-TCS-91.pdf Time] | ||
|- | |- | ||
| [[Shuji Tsukiyama, Mikio Ide, Hiromu Ariyoshi, and Isao Shirakawa (Enumerating Maximal Cliques, arbitrary graph Clique Problems)|Shuji Tsukiyama, Mikio Ide, Hiromu Ariyoshi, and Isao Shirakawa]] || 1977 || $O(nm)$ per clique || $O(m)$ | | [[Shuji Tsukiyama, Mikio Ide, Hiromu Ariyoshi, and Isao Shirakawa (Enumerating Maximal Cliques, arbitrary graph Clique Problems)|Shuji Tsukiyama, Mikio Ide, Hiromu Ariyoshi, and Isao Shirakawa]] || 1977 || $O(nm)$ per clique || $O(m)$ || Exact || Deterministic || [https://www.proquest.com/docview/918487776?pq-origsite=gscholar&fromopenview=true Time] | ||
|- | |- | ||
| [[Kazuhisa Makino, Takeaki Uno; Section 5 (Enumerating Maximal Cliques, arbitrary graph Clique Problems)|Kazuhisa Makino, Takeaki Uno; Section 5]] || 2004 || $O(n^{\omega})$ per clique where omega is the exponent on matrix multiplication || $O(n^{2})$ | | [[Kazuhisa Makino, Takeaki Uno; Section 5 (Enumerating Maximal Cliques, arbitrary graph Clique Problems)|Kazuhisa Makino, Takeaki Uno; Section 5]] || 2004 || $O(n^{\omega})$ per clique where omega is the exponent on matrix multiplication || $O(n^{2})$ || Exact || Deterministic || [https://link.springer.com/chapter/10.1007/978-3-540-27810-8_23 Time & Space] | ||
|- | |- | ||
| [[Kazuhisa Makino, Takeaki Uno; Section 6 (Enumerating Maximal Cliques, arbitrary graph Clique Problems)|Kazuhisa Makino, Takeaki Uno; Section 6]] || 2004 || $O(delta^{4})$ || $O(n+m)$ auxiliary(?) || Exact || Deterministic || [https://link.springer.com/chapter/10.1007/978-3-540-27810-8_23 Time & Space] | | [[Kazuhisa Makino, Takeaki Uno; Section 6 (Enumerating Maximal Cliques, arbitrary graph Clique Problems)|Kazuhisa Makino, Takeaki Uno; Section 6]] || 2004 || $O(delta^{4})$ || $O(n+m)$ auxiliary(?) || Exact || Deterministic || [https://link.springer.com/chapter/10.1007/978-3-540-27810-8_23 Time & Space] | ||
Revision as of 09:22, 10 April 2023
Description
A maximal clique (complete subgraph) is a clique that is not contained in any other clique. The goal here is to enumerate such maximal cliques in a given graph.
Related Problems
Related: k-Clique, Exact k-Clique, Min-Weight k-Clique, Max-Weight k-Clique
Parameters
$n$: number of vertices
$m$: number of edges
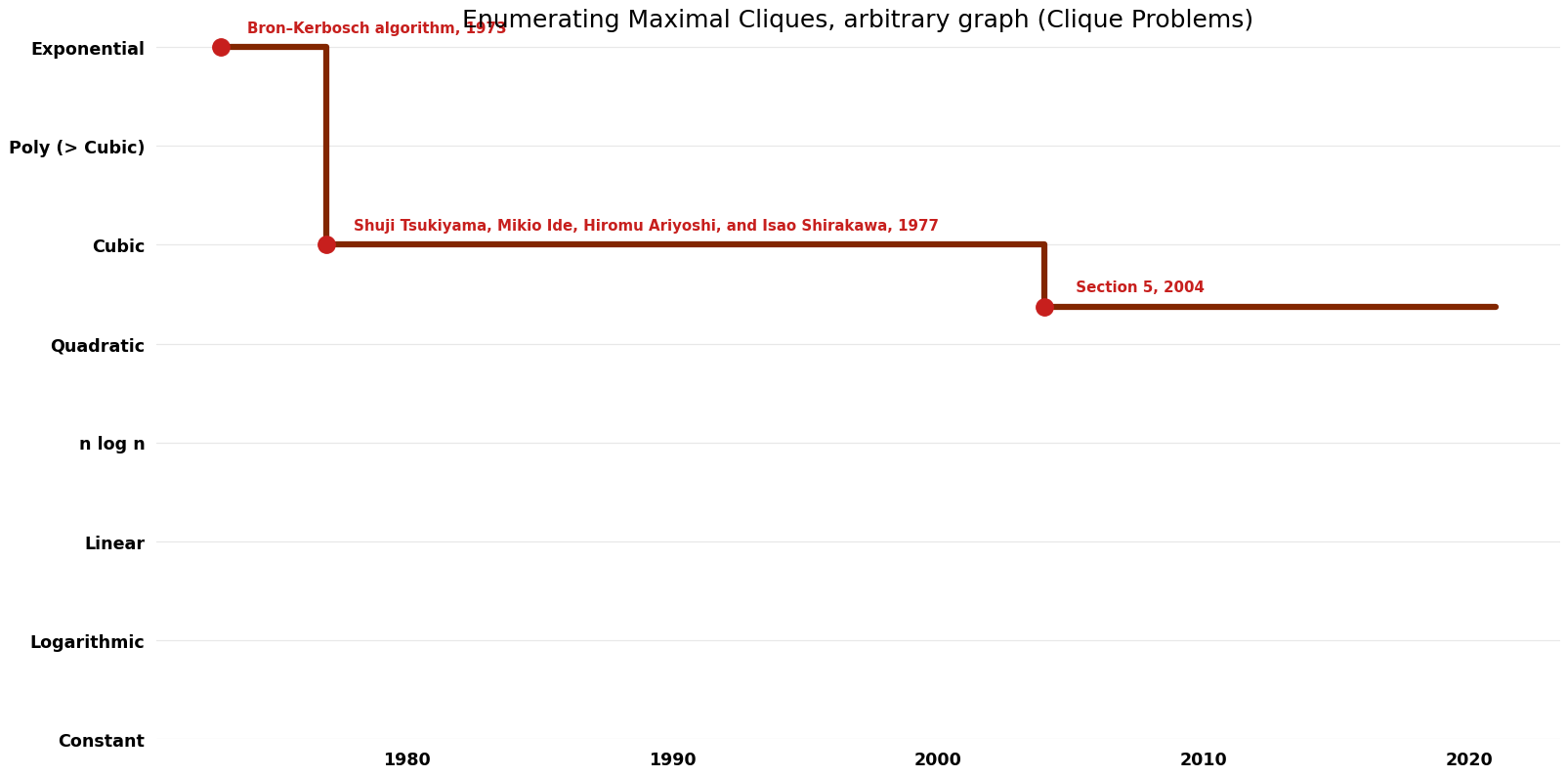
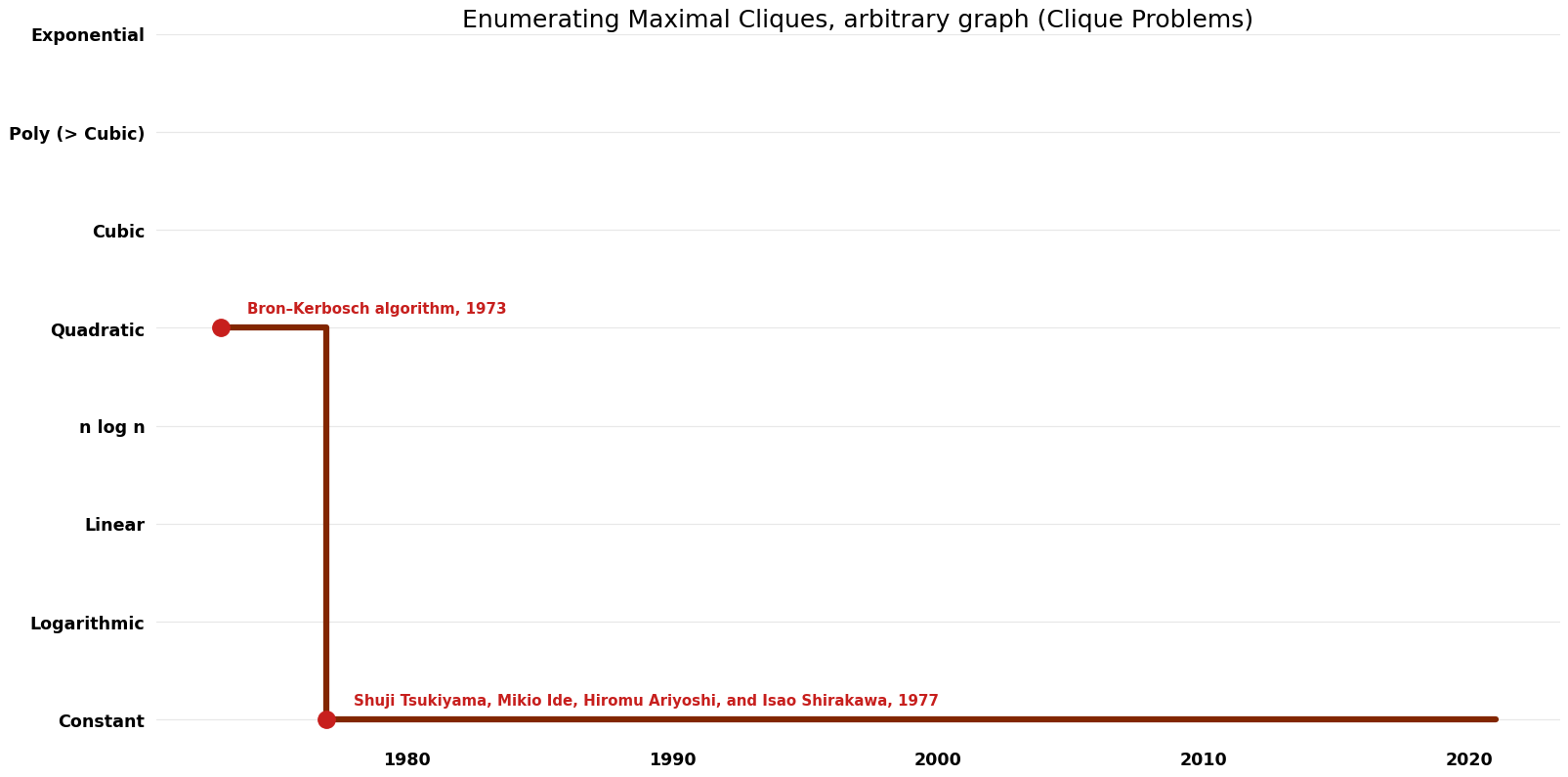
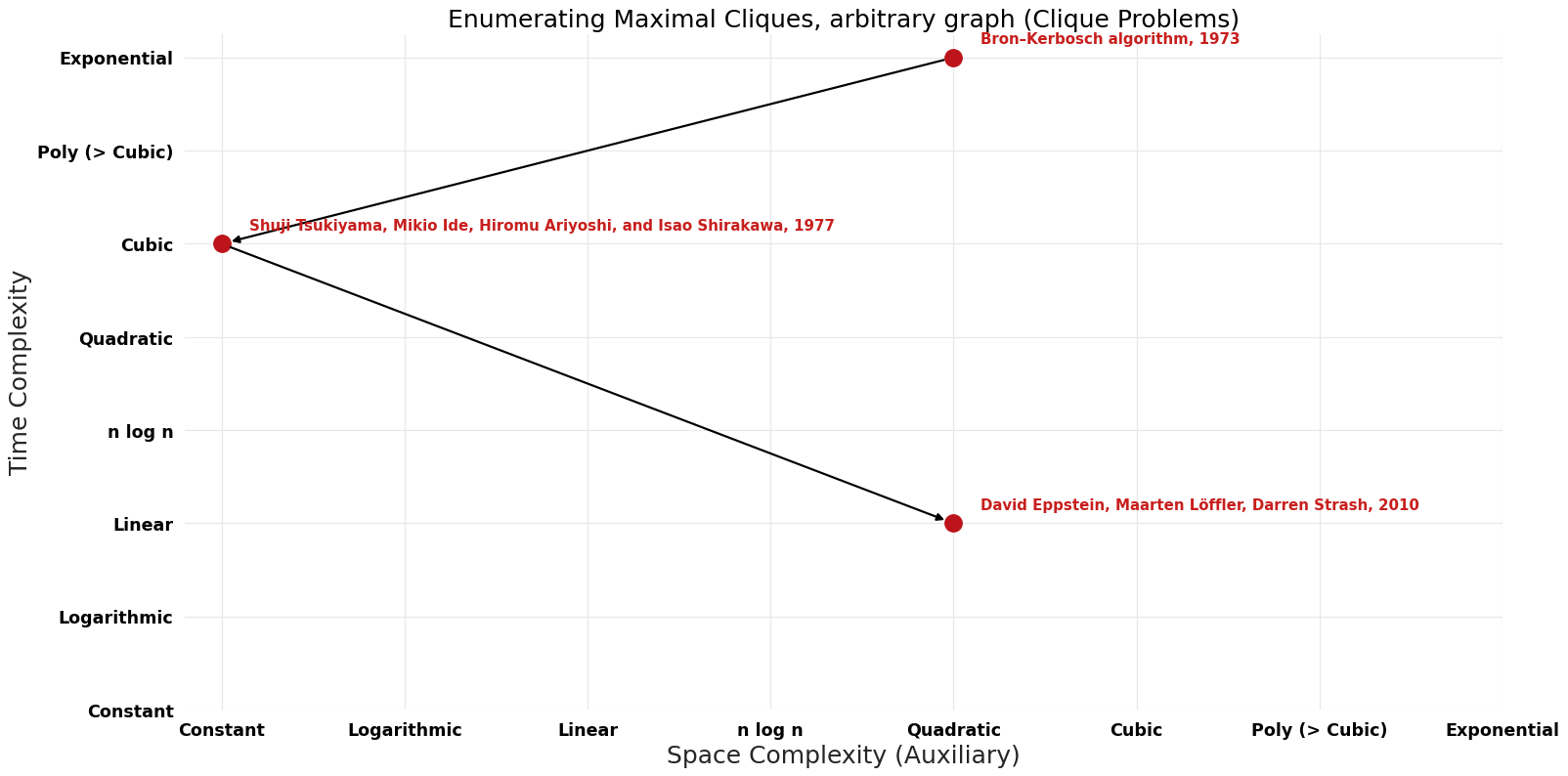
Table of Algorithms
| Name | Year | Time | Space | Approximation Factor | Model | Reference |
|---|---|---|---|---|---|---|
| Bron–Kerbosch algorithm | 1973 | $O({3}^{(n/{3})})$ | $O(n^{2})$? | Exact | Deterministic | Time |
| Akkoyunlu; E. A. | 1973 | $O({3}^{(n/{3})$}) | $O(n^{2})$? | Exact | Deterministic | Time |
| Tomita; Tanaka & Takahashi | 2006 | $O({3}^{(n/{3})$}) | $O(n^{2})$? | Exact | Deterministic | Time |
| Segundo; Artieda; Strash Parallel | 2011 | $O({3}^{(n/{3})})$ total work? (previously this cell said $O(n^{4})$) | $O(n^{2})$ auxiliary?? | Exact | Parallel | Time |
| David Eppstein, Maarten Löffler, Darren Strash | 2010 | $O(dn {3}^{(d/{3})})$ | $O(n^{2})$? | Exact | Deterministic | Time |
| Chiba and Nishizeki | 1985 | $O(a(G)*m)$ per clique | $O(m)$ | Exact | Deterministic | Time & Space |
| M. Chrobak and D. Eppstein | 1989 | $O(n d^{2} {2}^d)$ | $O(n)$? | Exact | Deterministic | Time |
| Shuji Tsukiyama, Mikio Ide, Hiromu Ariyoshi, and Isao Shirakawa | 1977 | $O(nm)$ per clique | $O(m)$ | Exact | Deterministic | Time |
| Kazuhisa Makino, Takeaki Uno; Section 5 | 2004 | $O(n^{\omega})$ per clique where omega is the exponent on matrix multiplication | $O(n^{2})$ | Exact | Deterministic | Time & Space |
| Kazuhisa Makino, Takeaki Uno; Section 6 | 2004 | $O(delta^{4})$ | $O(n+m)$ auxiliary(?) | Exact | Deterministic | Time & Space |