Cycle Detection: Difference between revisions
Jump to navigation
Jump to search
No edit summary |
No edit summary |
||
| Line 6: | Line 6: | ||
== Parameters == | == Parameters == | ||
t_f: time to perform one evaluation of f | $t_f$: time to perform one evaluation of $f$ | ||
\mu: the starting index of the cycle | $\mu$: the starting index of the cycle | ||
\lambda: the period of the cycle | $\lambda$: the period of the cycle | ||
M: number of values stored | $M$: number of values stored | ||
== Table of Algorithms == | == Table of Algorithms == | ||
| Line 22: | Line 22: | ||
|- | |- | ||
| [[Sedgewick; Szymanski; and Yao ( Cycle Detection)|Sedgewick; Szymanski; and Yao]] || 1982 || $(\mu + \lambda)({1}+\Theta({1}/sqrt(M)))$ || M || Exact || Deterministic || [https://epubs.siam.org/doi/abs/10.1137/0211030?journalCode=smjcat Time & Space] | | [[Sedgewick; Szymanski; and Yao (Cycle Detection Cycle Detection)|Sedgewick; Szymanski; and Yao]] || 1982 || $(\mu + \lambda)({1}+\Theta({1}/sqrt(M)))$ || M || Exact || Deterministic || [https://epubs.siam.org/doi/abs/10.1137/0211030?journalCode=smjcat Time & Space] | ||
|- | |- | ||
| [[Nivasch ( Cycle Detection)|Nivasch]] || 2004 || $O(\mu + \lambda)$ || $O( | | [[Nivasch (Cycle Detection Cycle Detection)|Nivasch]] || 2004 || $O(\mu + \lambda)$ || $O(\log\mu)$ || Exact || Deterministic || [https://drive.google.com/file/d/16H_lrjeaBJqWvcn07C_w-6VNHldJ-ZZl/view Time] & [https://www.gabrielnivasch.org/fun/cycle-detection Space] | ||
|- | |- | ||
| [[Floyd's tortoise and hare algorithm ( Cycle Detection)|Floyd's tortoise and hare algorithm]] || 1967 || $O((\lambda + \mu)$ t_f) || $O({1})$ || Exact || Deterministic || [http://pds7.egloos.com/pds/200801/07/29/p636-floyd.pdf Time] | | [[Floyd's tortoise and hare algorithm ( Cycle Detection)|Floyd's tortoise and hare algorithm]] || 1967 || $O((\lambda + \mu)$ t_f) || $O({1})$ || Exact || Deterministic || [http://pds7.egloos.com/pds/200801/07/29/p636-floyd.pdf Time] | ||
Revision as of 08:52, 10 April 2023
Description
Cycle detection or cycle finding is the algorithmic problem of finding a cycle in a sequence of iterated function values.
Parameters
$t_f$: time to perform one evaluation of $f$
$\mu$: the starting index of the cycle
$\lambda$: the period of the cycle
$M$: number of values stored
Table of Algorithms
| Name | Year | Time | Space | Approximation Factor | Model | Reference |
|---|---|---|---|---|---|---|
| Sedgewick; Szymanski; and Yao | 1982 | $(\mu + \lambda)({1}+\Theta({1}/sqrt(M)))$ | M | Exact | Deterministic | Time & Space |
| Nivasch | 2004 | $O(\mu + \lambda)$ | $O(\log\mu)$ | Exact | Deterministic | Time & Space |
| Floyd's tortoise and hare algorithm | 1967 | $O((\lambda + \mu)$ t_f) | $O({1})$ | Exact | Deterministic | Time |
| Brent's algorithm | 1973 | $O((\lambda + \mu)$ t_f) | $O({1})$ | Exact | Deterministic | Time |
| Gosper's algorithm | 1978 | $O((\lambda + \mu)$ log(\lambda + \mu) t_f) | \Theta(log(\mu + \lambda)) | Exact | Deterministic | Time & Space |
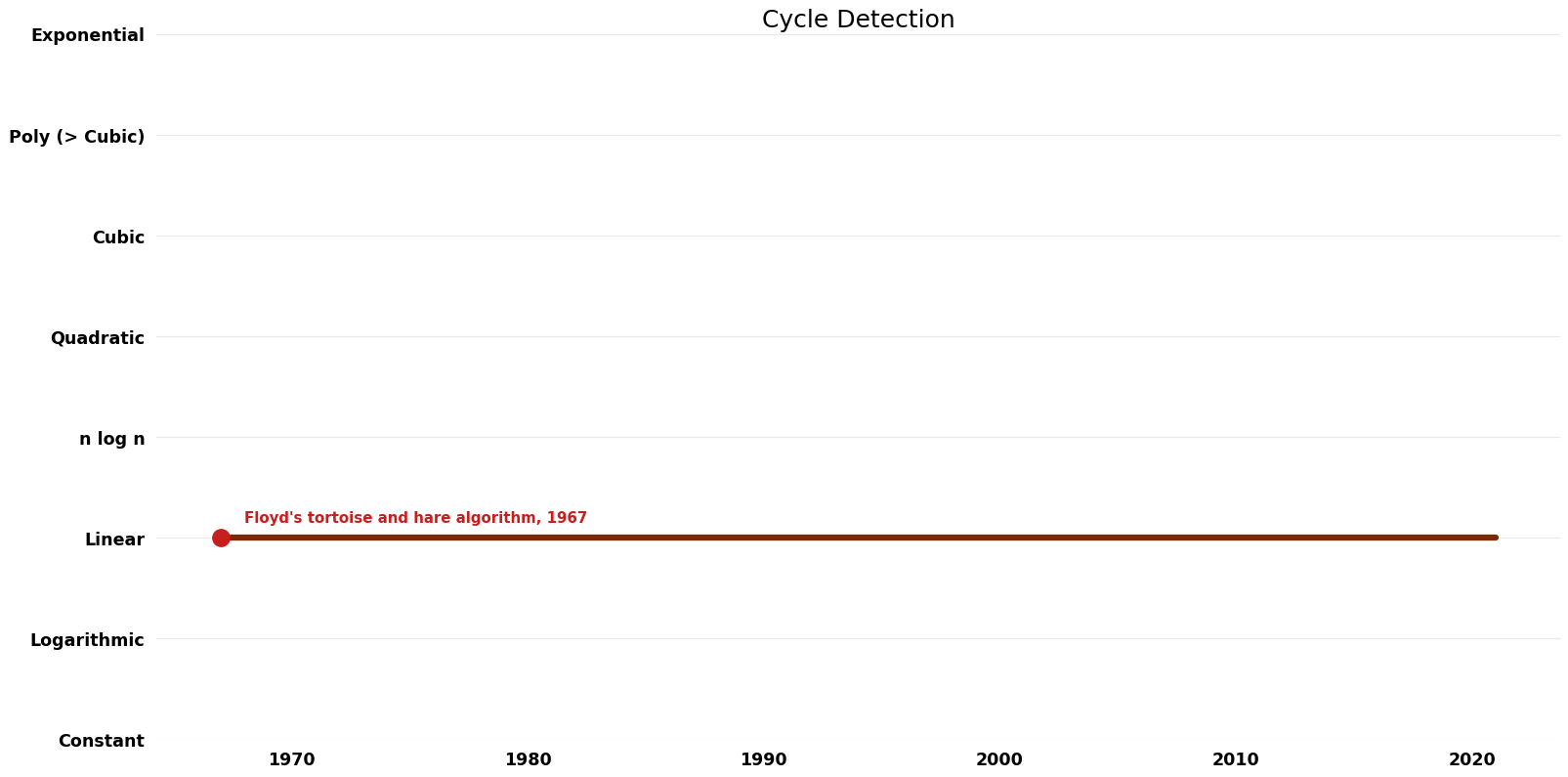
Time Complexity Graph
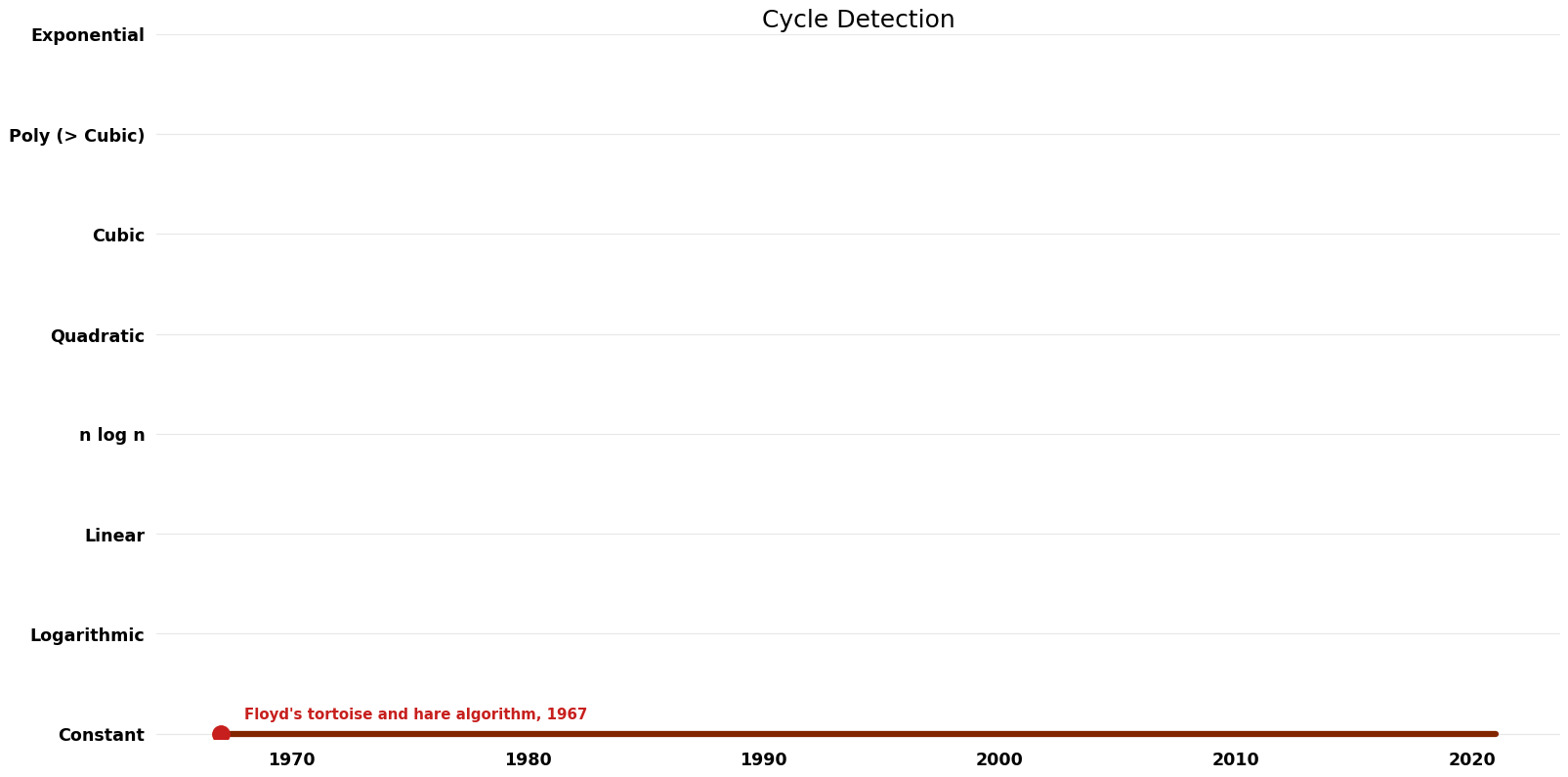
Space Complexity Graph
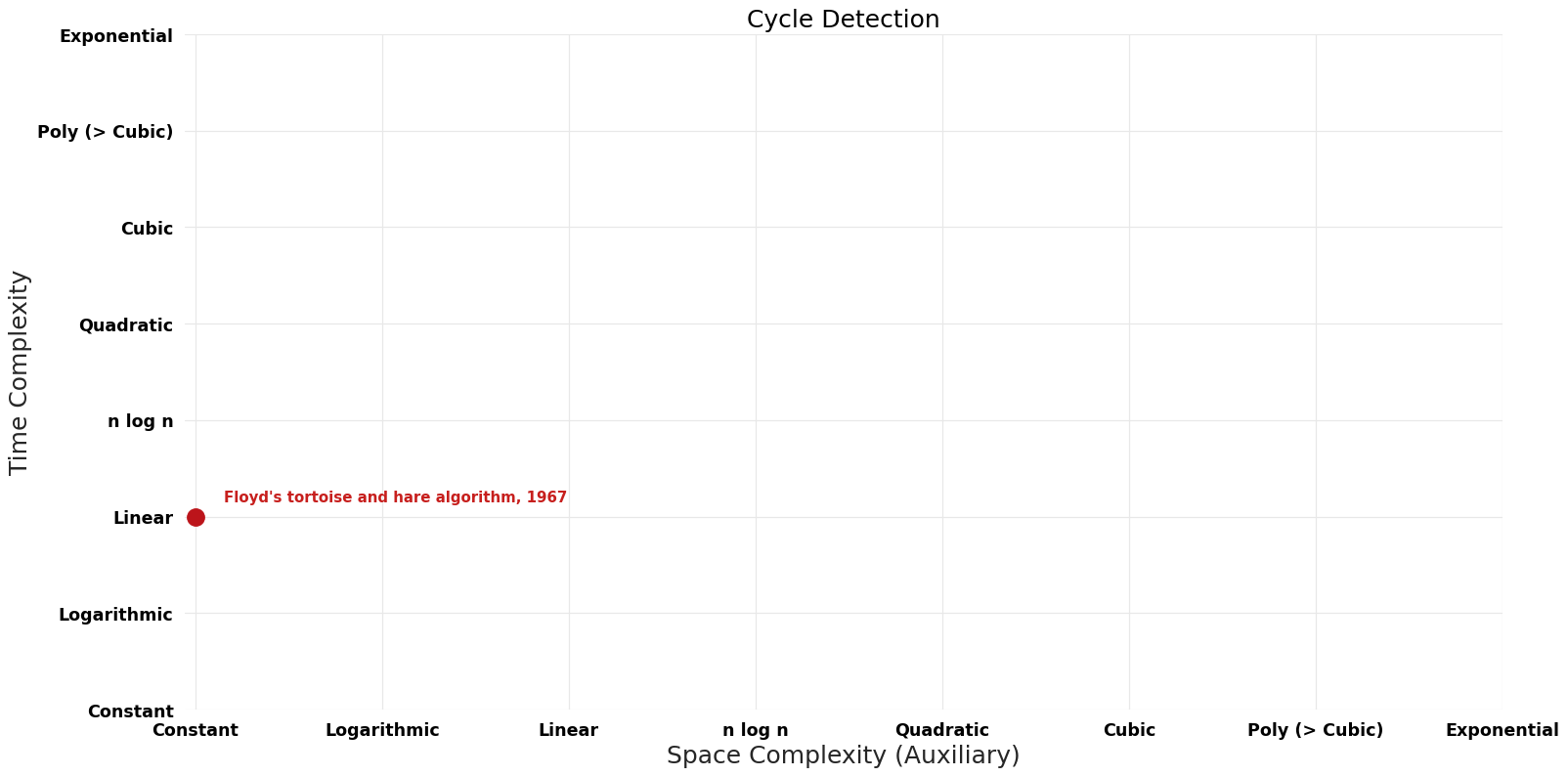
Time-Space Tradeoff
References/Citation
https://www.sciencedirect.com/science/article/pii/0304397585900441?via%3Dihub