Inexact Laplacian Solver: Difference between revisions
Jump to navigation
Jump to search
(Created page with "{{DISPLAYTITLE:Inexact Laplacian Solver (SDD Systems Solvers)}} == Description == This problem refers to solving equations of the form $Lx = b$ where $L$ is a Laplacian of a graph. In other words, this is solving equations of the form $Ax = b$ for a SDD matrix $A$. This variation of the problem permits some error. == Related Problems == Related: Exact Laplacian Solver == Parameters == No parameters found. == Table of Algorithms == {| class="wikitable sort...") |
No edit summary |
||
| (One intermediate revision by the same user not shown) | |||
| Line 12: | Line 12: | ||
== Parameters == | == Parameters == | ||
$n$: dimension of matrix | |||
== Table of Algorithms == | == Table of Algorithms == | ||
| Line 22: | Line 22: | ||
|- | |- | ||
| [[Spielman, Teng (Inexact Laplacian Solver SDD Systems Solvers)|Spielman, Teng ]] || 2004 || $O(m log^c n)$ || $O(n)$ || \epsilon || Deterministic || [https://dl.acm.org/doi/pdf/10.1145/1007352.1007372?casa_token=k60CrC_UJp0AAAAA:yGVve4fRNbftRM0P7aaEbq8OIlxa4nRy8-CjZErlGrBwBfPEt0ECHGYc8Ei48rdA9W9NoY73xC2W Time] | | [[Spielman, Teng (Inexact Laplacian Solver SDD Systems Solvers)|Spielman, Teng ]] || 2004 || $O(m \log^c n)$ || $O(n)$ || \epsilon || Deterministic || [https://dl.acm.org/doi/pdf/10.1145/1007352.1007372?casa_token=k60CrC_UJp0AAAAA:yGVve4fRNbftRM0P7aaEbq8OIlxa4nRy8-CjZErlGrBwBfPEt0ECHGYc8Ei48rdA9W9NoY73xC2W Time] | ||
|- | |- | ||
| [[Vaidya (Inexact Laplacian Solver SDD Systems Solvers)|Vaidya]] || 1990 || $O(mn^{({3}/{4})$}) || $O(n)$ || \epsilon || Deterministic || | | [[Vaidya (Inexact Laplacian Solver SDD Systems Solvers)|Vaidya]] || 1990 || $O(mn^{({3}/{4})$}) || $O(n)$ || \epsilon || Deterministic || | ||
| Line 28: | Line 28: | ||
| [[Gremban; Miller; Zagha (Inexact Laplacian Solver SDD Systems Solvers)|Gremban; Miller; Zagha]] || 1995 || $O(n^{2})$ || $O(n^{2})$ || ? || Deterministic || [https://www.cs.cmu.edu/~glmiller/Publications/Papers/GrMiZa94-tr.pdf Time & Space] | | [[Gremban; Miller; Zagha (Inexact Laplacian Solver SDD Systems Solvers)|Gremban; Miller; Zagha]] || 1995 || $O(n^{2})$ || $O(n^{2})$ || ? || Deterministic || [https://www.cs.cmu.edu/~glmiller/Publications/Papers/GrMiZa94-tr.pdf Time & Space] | ||
|- | |- | ||
| [[Bern; Gilbert; Hendrickson (Inexact Laplacian Solver SDD Systems Solvers)|Bern; Gilbert; Hendrickson]] || 2006 || $O(n | | [[Bern; Gilbert; Hendrickson (Inexact Laplacian Solver SDD Systems Solvers)|Bern; Gilbert; Hendrickson]] || 2006 || $O(n \log \log n)$ || || Exact || Deterministic || [https://dl.acm.org/citation.cfm?id=1117896 Time] | ||
|- | |- | ||
| [[Boman; Hendrickson (Inexact Laplacian Solver SDD Systems Solvers)|Boman; Hendrickson]] || 2003 || $\tilde{O}(mn^{({1}/{2})})$ || || \epsilon || Deterministic || [https://epubs.siam.org/doi/10.1137/S0895479801390637 Time] | | [[Boman; Hendrickson (Inexact Laplacian Solver SDD Systems Solvers)|Boman; Hendrickson]] || 2003 || $\tilde{O}(mn^{({1}/{2})})$ || || \epsilon || Deterministic || [https://epubs.siam.org/doi/10.1137/S0895479801390637 Time] | ||
|- | |- | ||
| [[Boman; Chen; Hendrickson; Toledo (Inexact Laplacian Solver SDD Systems Solvers)|Boman; Chen; Hendrickson; Toledo]] || 2004 || $O(n log({1}/ϵ)$ ) || $O(n)$ || \epsilon || Deterministic || [https://onlinelibrary.wiley.com/doi/abs/10.1002/nla.343 Time] | | [[Boman; Chen; Hendrickson; Toledo (Inexact Laplacian Solver SDD Systems Solvers)|Boman; Chen; Hendrickson; Toledo]] || 2004 || $O(n \log({1}/ϵ)$ ) || $O(n)$ || \epsilon || Deterministic || [https://onlinelibrary.wiley.com/doi/abs/10.1002/nla.343 Time] | ||
|- | |- | ||
| [[Koutis; Miller and Peng (Inexact Laplacian Solver SDD Systems Solvers)|Koutis; Miller and Peng]] || 2010 || $\tilde{O}(m log n)$ || $O(n)$ || \epsilon || Deterministic || [https://arxiv.org/abs/1102.4842 Time] | | [[Koutis; Miller and Peng (Inexact Laplacian Solver SDD Systems Solvers)|Koutis; Miller and Peng]] || 2010 || $\tilde{O}(m \log n)$ || $O(n)$ || \epsilon || Deterministic || [https://arxiv.org/abs/1102.4842 Time] | ||
|- | |- | ||
| [[Koutis; Miller and Peng (Inexact Laplacian Solver SDD Systems Solvers)|Koutis; Miller and Peng]] || 2011 || $\tilde{O}(m log n)$ || $O(n)$ || \epsilon || Deterministic || [https://arxiv.org/abs/1003.2958 Time] | | [[Koutis; Miller and Peng (Inexact Laplacian Solver SDD Systems Solvers)|Koutis; Miller and Peng]] || 2011 || $\tilde{O}(m \log n)$ || $O(n)$ || \epsilon || Deterministic || [https://arxiv.org/abs/1003.2958 Time] | ||
|- | |- | ||
| [[Blelloch; Koutis; Miller; Tangwongsan (Inexact Laplacian Solver SDD Systems Solvers)|Blelloch; Koutis; Miller; Tangwongsan]] || 2010 || $O(n | | [[Blelloch; Koutis; Miller; Tangwongsan (Inexact Laplacian Solver SDD Systems Solvers)|Blelloch; Koutis; Miller; Tangwongsan]] || 2010 || $O(n \log n)$ || m + $O(n/\log n)$ || ? || Deterministic || [https://ieeexplore.ieee.org/document/5644892 Time] & [https://www.cs.cmu.edu/afs/cs.cmu.edu/Web/People/jkoutis/papers/SC10-paper.pdf Space] | ||
|- | |- | ||
| [[Briggs; Henson; McCormick ( SDD Systems Solvers)|Briggs; Henson; McCormick]] || 2000 || $O(n^{1.{2}5} | | [[Briggs; Henson; McCormick ( SDD Systems Solvers)|Briggs; Henson; McCormick]] || 2000 || $O(n^{1.{2}5} \log \log n)$ || || Exact || Deterministic || [http://www.math.ust.hk/~mamu/courses/531/tutorial_with_corrections.pdf Time] | ||
|- | |- | ||
| [[Kelner; Orecchia; Sidford; Zhu (Inexact Laplacian Solver SDD Systems Solvers)|Kelner; Orecchia; Sidford; Zhu]] || 2013 || $O(m log^{2} (n)$ | | [[Kelner; Orecchia; Sidford; Zhu (Inexact Laplacian Solver SDD Systems Solvers)|Kelner; Orecchia; Sidford; Zhu]] || 2013 || $O(m \log^{2} (n)$ \log \log n) || $O(n)$ || \epsilon || Deterministic || [https://arxiv.org/pdf/1301.6628.pdf Time] | ||
|- | |- | ||
| [[Lee; Peng; Spielman (Inexact Laplacian Solver SDD Systems Solvers)|Lee; Peng; Spielman]] || 2015 || $O(n)$ || $O(n)$ || The sparse Cholesky decomposition is a 2-approximation || Deterministic || [https://arxiv.org/abs/1506.08204 Time] | | [[Lee; Peng; Spielman (Inexact Laplacian Solver SDD Systems Solvers)|Lee; Peng; Spielman]] || 2015 || $O(n)$ || $O(n)$ || The sparse Cholesky decomposition is a 2-approximation || Deterministic || [https://arxiv.org/abs/1506.08204 Time] | ||
|- | |- | ||
| [[Daitch; Spielman (Inexact Laplacian Solver SDD Systems Solvers)|Daitch; Spielman]] || 2007 || $O(n^{5/4} (log^{2} (n)$ | | [[Daitch; Spielman (Inexact Laplacian Solver SDD Systems Solvers)|Daitch; Spielman]] || 2007 || $O(n^{5/4} (\log^{2} (n)$ \log\log n)^{3/4} \log({1}/ϵ)) || $O(n)$ || \epsilon || Deterministic || [https://arxiv.org/abs/cs/0703119 Time] | ||
|- | |- | ||
|} | |} | ||
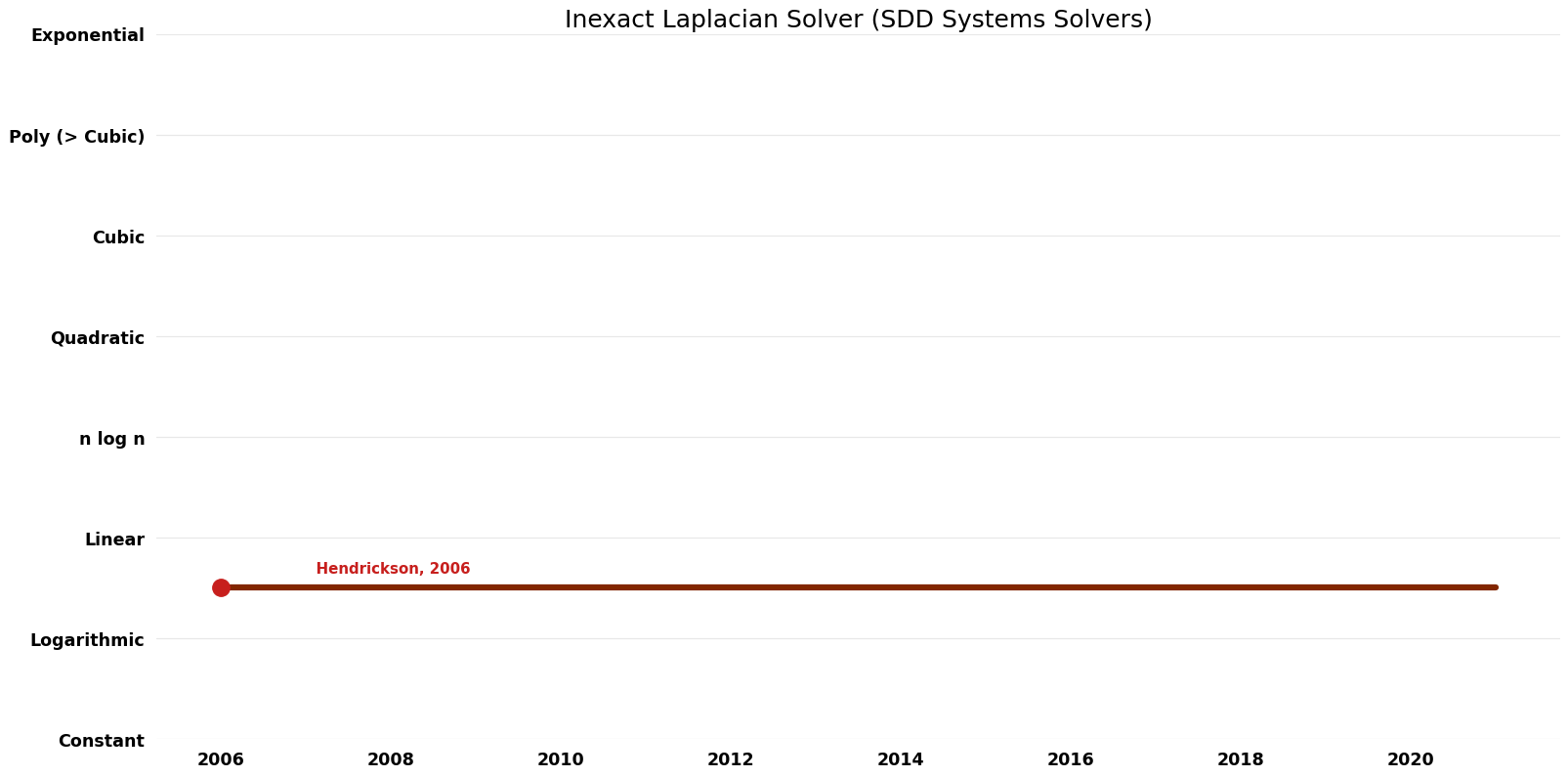
== Time Complexity | == Time Complexity Graph == | ||
[[File:SDD Systems Solvers - Inexact Laplacian Solver - Time.png|1000px]] | [[File:SDD Systems Solvers - Inexact Laplacian Solver - Time.png|1000px]] | ||
Latest revision as of 08:52, 10 April 2023
Description
This problem refers to solving equations of the form $Lx = b$ where $L$ is a Laplacian of a graph. In other words, this is solving equations of the form $Ax = b$ for a SDD matrix $A$.
This variation of the problem permits some error.
Related Problems
Related: Exact Laplacian Solver
Parameters
$n$: dimension of matrix
Table of Algorithms
| Name | Year | Time | Space | Approximation Factor | Model | Reference |
|---|---|---|---|---|---|---|
| Spielman, Teng | 2004 | $O(m \log^c n)$ | $O(n)$ | \epsilon | Deterministic | Time |
| Vaidya | 1990 | $O(mn^{({3}/{4})$}) | $O(n)$ | \epsilon | Deterministic | |
| Gremban; Miller; Zagha | 1995 | $O(n^{2})$ | $O(n^{2})$ | ? | Deterministic | Time & Space |
| Bern; Gilbert; Hendrickson | 2006 | $O(n \log \log n)$ | Exact | Deterministic | Time | |
| Boman; Hendrickson | 2003 | $\tilde{O}(mn^{({1}/{2})})$ | \epsilon | Deterministic | Time | |
| Boman; Chen; Hendrickson; Toledo | 2004 | $O(n \log({1}/ϵ)$ ) | $O(n)$ | \epsilon | Deterministic | Time |
| Koutis; Miller and Peng | 2010 | $\tilde{O}(m \log n)$ | $O(n)$ | \epsilon | Deterministic | Time |
| Koutis; Miller and Peng | 2011 | $\tilde{O}(m \log n)$ | $O(n)$ | \epsilon | Deterministic | Time |
| Blelloch; Koutis; Miller; Tangwongsan | 2010 | $O(n \log n)$ | m + $O(n/\log n)$ | ? | Deterministic | Time & Space |
| Briggs; Henson; McCormick | 2000 | $O(n^{1.{2}5} \log \log n)$ | Exact | Deterministic | Time | |
| Kelner; Orecchia; Sidford; Zhu | 2013 | $O(m \log^{2} (n)$ \log \log n) | $O(n)$ | \epsilon | Deterministic | Time |
| Lee; Peng; Spielman | 2015 | $O(n)$ | $O(n)$ | The sparse Cholesky decomposition is a 2-approximation | Deterministic | Time |
| Daitch; Spielman | 2007 | $O(n^{5/4} (\log^{2} (n)$ \log\log n)^{3/4} \log({1}/ϵ)) | $O(n)$ | \epsilon | Deterministic | Time |