Discrete Fourier Transform: Difference between revisions
Jump to navigation
Jump to search
No edit summary |
No edit summary |
||
| Line 48: | Line 48: | ||
[[File:Discrete Fourier Transform - Space.png|1000px]] | [[File:Discrete Fourier Transform - Space.png|1000px]] | ||
== Space | == Time-Space Tradeoff == | ||
[[File:Discrete Fourier Transform - Pareto Frontier.png|1000px]] | [[File:Discrete Fourier Transform - Pareto Frontier.png|1000px]] | ||
Revision as of 15:44, 15 February 2023
Description
In mathematics, the discrete Fourier transform (DFT) converts a finite sequence of equally-spaced samples of a function into a same-length sequence of equally-spaced samples of the discrete-time Fourier transform (DTFT), which is a complex-valued function of frequency.
Parameters
$n$: length of the input data set
Table of Algorithms
| Name | Year | Time | Space | Approximation Factor | Model | Reference |
|---|---|---|---|---|---|---|
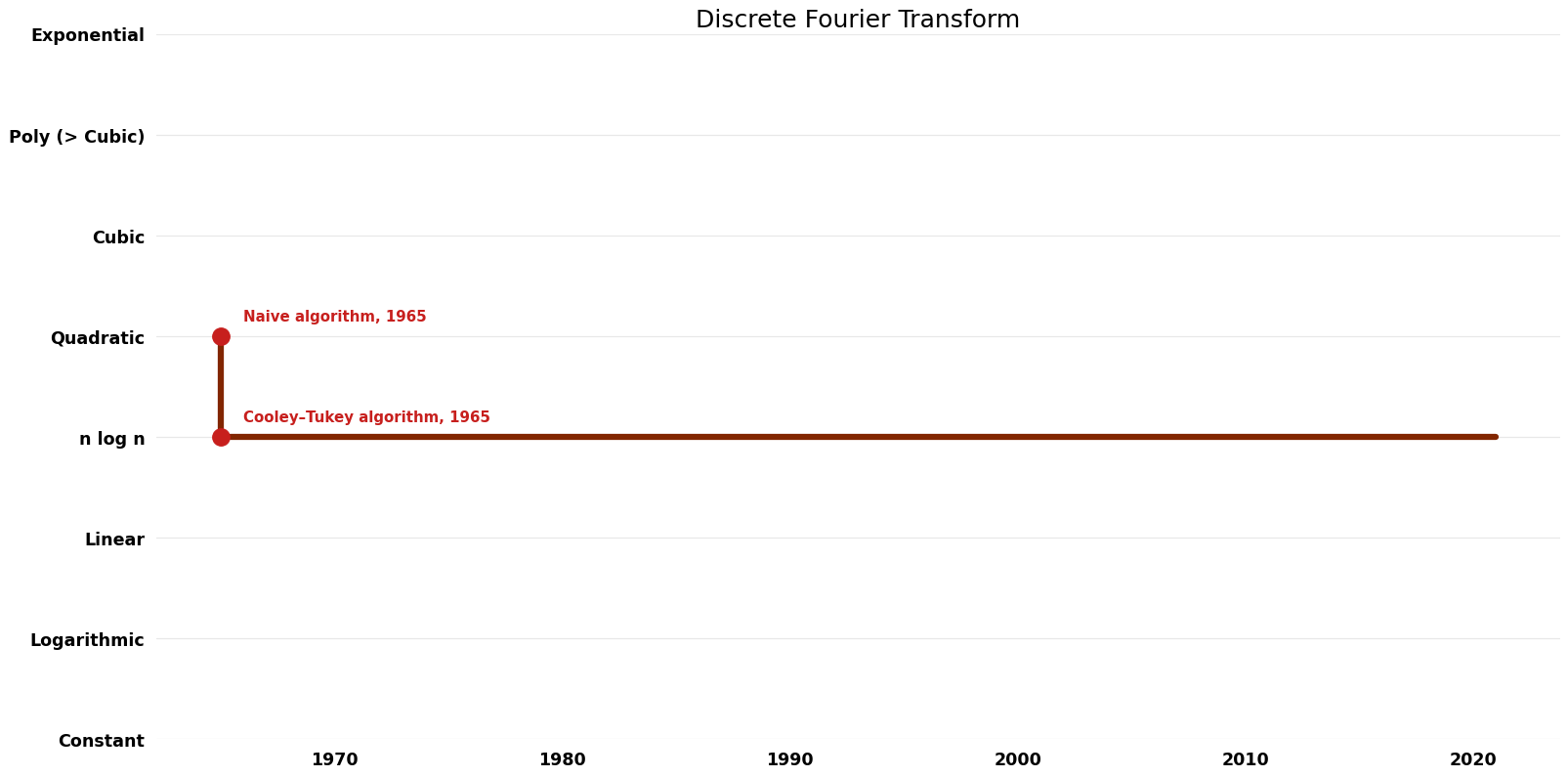
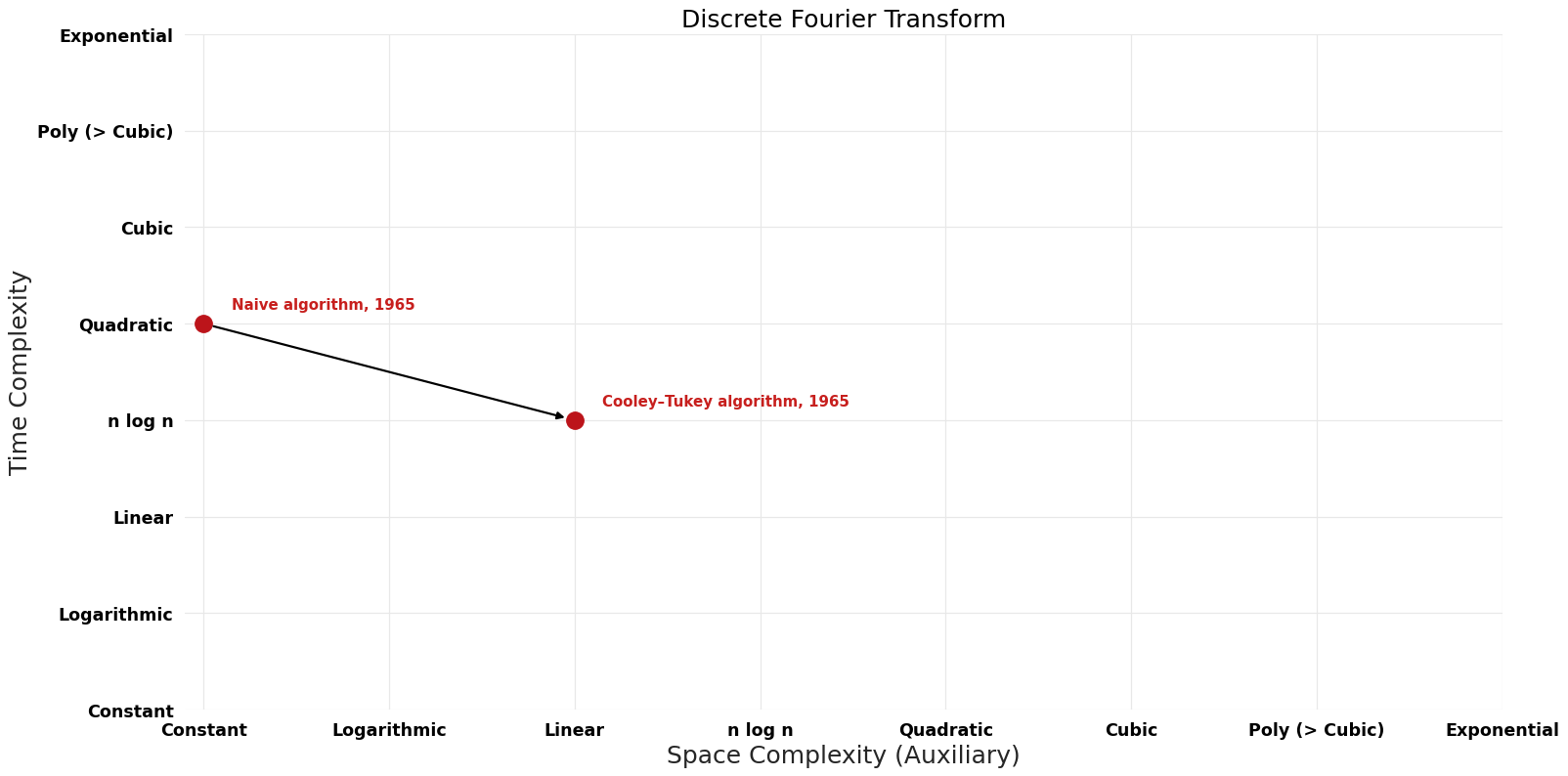
| Naive algorithm | 1965 | $O(n^{2})$ | $O({1})$ | Exact | Deterministic | |
| Cooley–Tukey algorithm | 1965 | $O(nlogn)$ | $O(n)$? | Exact | Deterministic | Time |
| Rader–Brenner algorithm | 1976 | $O(nlogn)$ | $O(n)$? | Exact | Deterministic | Time |
| Bruun's FFT algorithm | 1978 | $O(nlogn)$ | $O(n)$? | Exact | Deterministic | Time |
| Yavne Split Radix FFT algorithm | 1968 | $O(nlogn)$ | $O(n)$? | Exact | Deterministic | Time |
| Gentleman; Morven and Gordon Sande radix-4 algorithm | 1966 | $O(nlogn)$ | $O(n)$? | Exact | Deterministic | Time |
| Bergland; Glenn radix-8 algorithm | 1969 | $O(nlogn)$ | $O(n)$ | Exact | Deterministic | Time & Space |
| Extended Split Radix FFT algorithm | 2001 | $O(nlogn)$ | $O(n)$? | Exact | Deterministic | Time |
| Von zur Gathen-Gerhard additive FFT | 1996 | $O(n (logn)$^{2}) | $O(n)$ | Exact | Deterministic | Time & Space |
| Wang-Zhu-Cantor additive FFT | 1988 | $O(n(logn)$^{1.{58}5}) | $O(n)$? | Exact | Deterministic | Time |
| Gao’s additive FFT | 2010 | $O(n logn loglogn)$ | $O(n)$ | Exact | Deterministic | Time & Space |