Matrix Chain Ordering Problem: Difference between revisions
Jump to navigation
Jump to search
No edit summary |
No edit summary |
||
| Line 24: | Line 24: | ||
| [[Brute Force (Matrix Chain Ordering Problem Matrix Chain Multiplication)|Brute Force]] || 1940 || $O({4}^n)$ || $O(n)$ || Exact || Deterministic || | | [[Brute Force (Matrix Chain Ordering Problem Matrix Chain Multiplication)|Brute Force]] || 1940 || $O({4}^n)$ || $O(n)$ || Exact || Deterministic || | ||
|- | |- | ||
| [[Dynamic Programming Algorithm (S. S. Godbole) (Matrix Chain Ordering Problem Matrix Chain Multiplication)|Dynamic Programming Algorithm (S. S. Godbole)]] || 1953 || $O(n^{3})$ || $O(n^{2})$ || Exact || Deterministic || | | [[Dynamic Programming Algorithm (S. S. Godbole) (Matrix Chain Ordering Problem Matrix Chain Multiplication)|Dynamic Programming Algorithm (S. S. Godbole)]] || 1953 || $O(n^{3})$ || $O(n^{2})$ || Exact || Deterministic || [http://mitpress.mit.edu/9780262046305/introduction-to-algorithms/ Space] | ||
|- | |- | ||
| [[T. C. Hu ; M. T. Shing (Matrix Chain Ordering Problem Matrix Chain Multiplication)|T. C. Hu ; M. T. Shing]] || 1982 || $O(nlogn)$ || $O(n)$ || Exact || Deterministic || [https://citeseerx.ist.psu.edu/viewdoc/citations?doi=10.1.1.695.2923 Time] | | [[T. C. Hu ; M. T. Shing (Matrix Chain Ordering Problem Matrix Chain Multiplication)|T. C. Hu ; M. T. Shing]] || 1982 || $O(nlogn)$ || $O(n)$ || Exact || Deterministic || [https://citeseerx.ist.psu.edu/viewdoc/citations?doi=10.1.1.695.2923 Time] | ||
| Line 38: | Line 38: | ||
[[File:Matrix Chain Multiplication - Matrix Chain Ordering Problem - Space.png|1000px]] | [[File:Matrix Chain Multiplication - Matrix Chain Ordering Problem - Space.png|1000px]] | ||
== Space | == Time-Space Tradeoff == | ||
[[File:Matrix Chain Multiplication - Matrix Chain Ordering Problem - Pareto Frontier.png|1000px]] | [[File:Matrix Chain Multiplication - Matrix Chain Ordering Problem - Pareto Frontier.png|1000px]] | ||
Revision as of 15:39, 15 February 2023
Description
Matrix chain multiplication (or Matrix Chain Ordering Problem; MCOP) is an optimization problem. Given a sequence of matrices, the goal is to find the most efficient way to multiply these matrices.
Related Problems
Subproblem: Approximate MCOP, Matrix Chain Scheduling Problem
Related: Matrix Chain Scheduling Problem, Approximate MCSP
Parameters
$n$: number of matrices
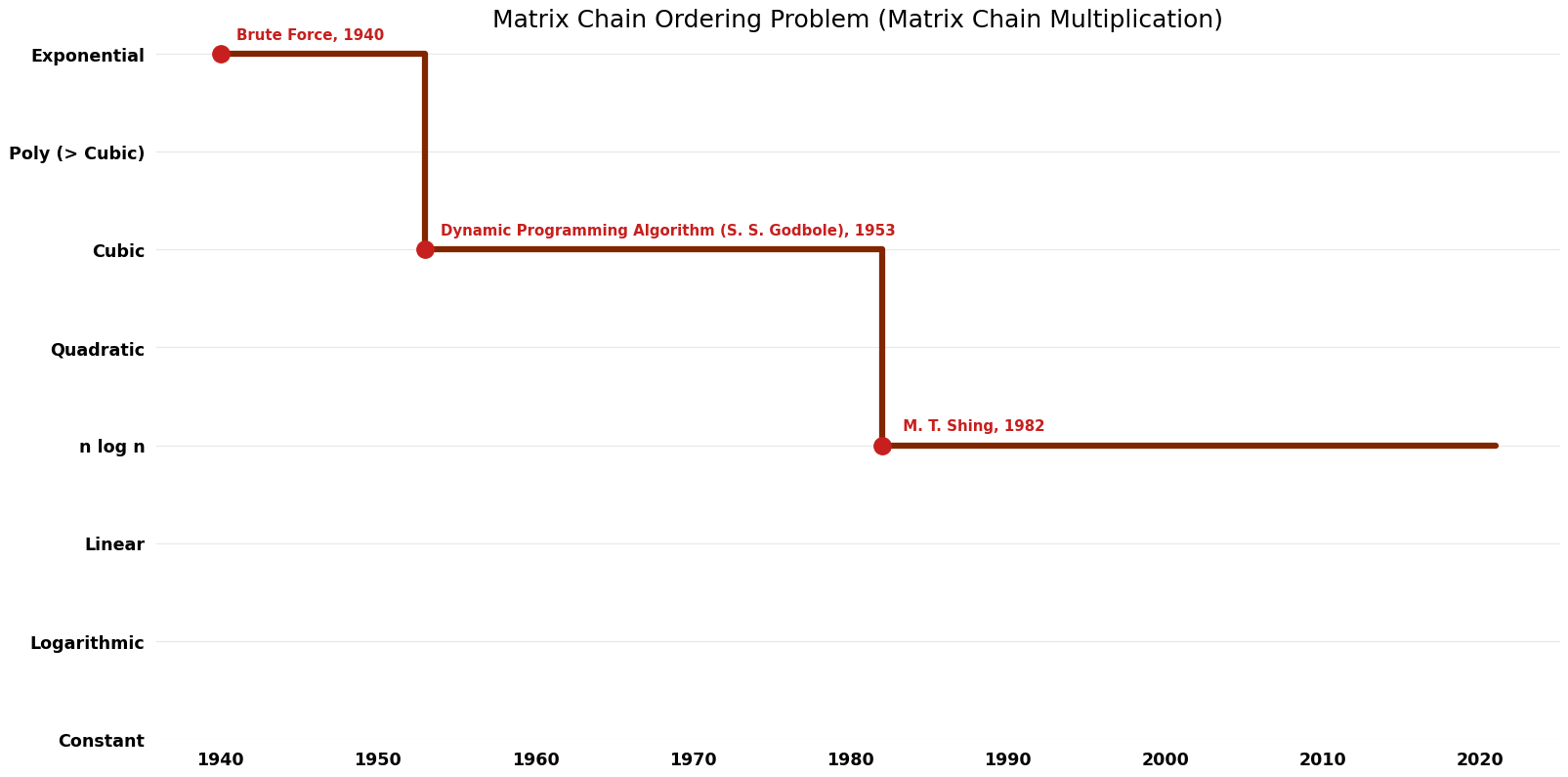
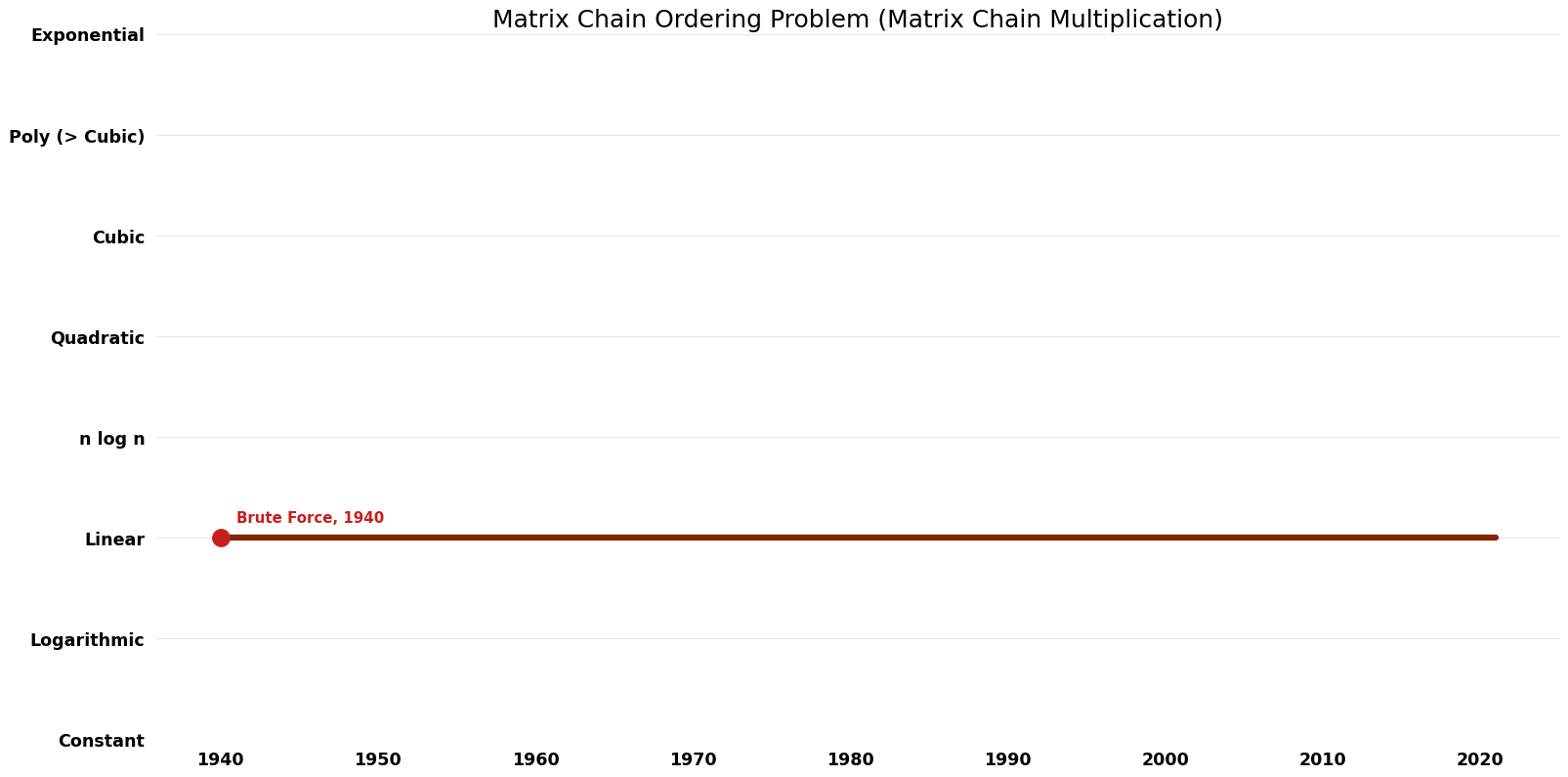
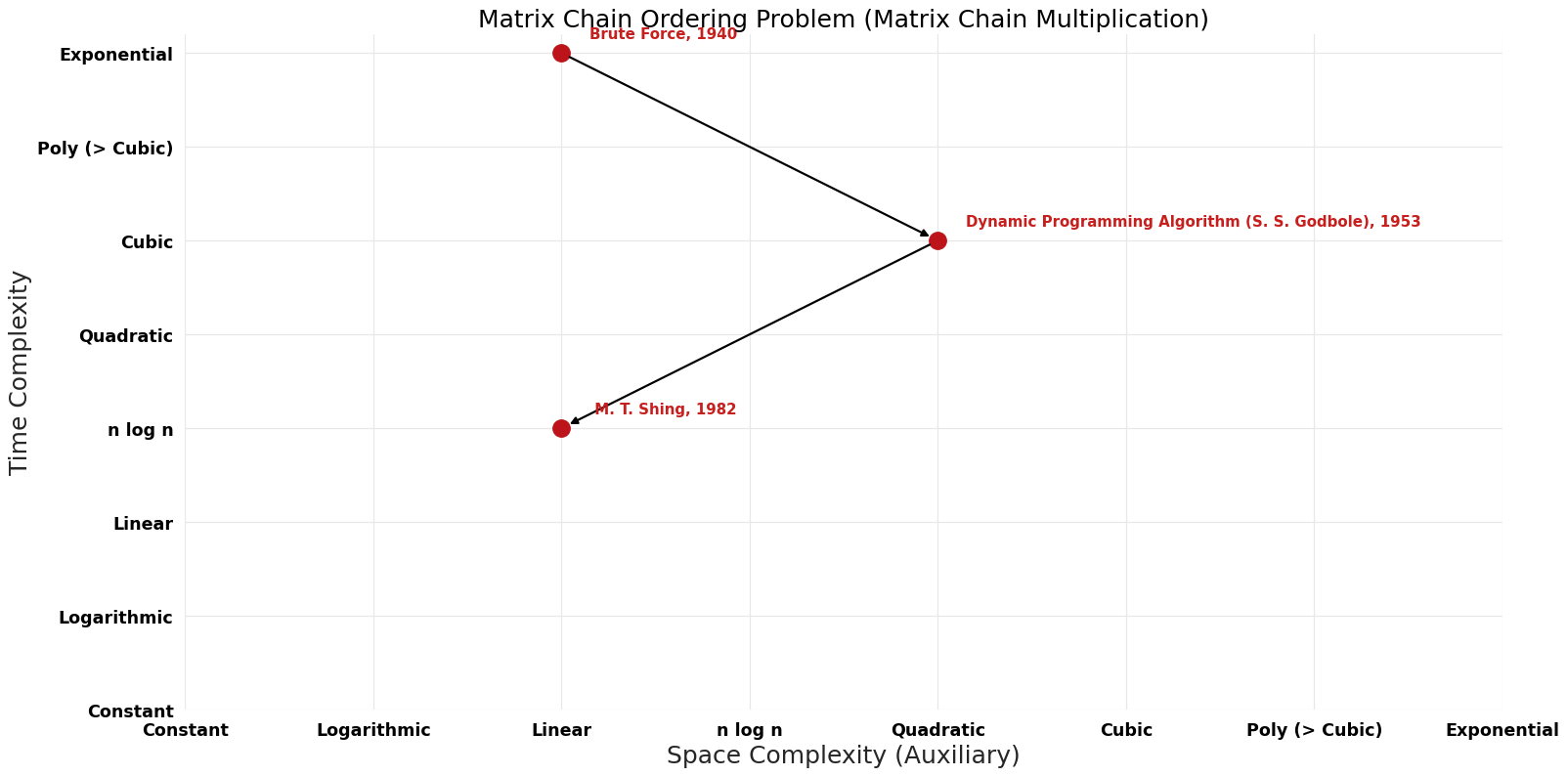
Table of Algorithms
| Name | Year | Time | Space | Approximation Factor | Model | Reference |
|---|---|---|---|---|---|---|
| Brute Force | 1940 | $O({4}^n)$ | $O(n)$ | Exact | Deterministic | |
| Dynamic Programming Algorithm (S. S. Godbole) | 1953 | $O(n^{3})$ | $O(n^{2})$ | Exact | Deterministic | Space |
| T. C. Hu ; M. T. Shing | 1982 | $O(nlogn)$ | $O(n)$ | Exact | Deterministic | Time |
Time Complexity Graph
Space Complexity Graph
Time-Space Tradeoff
References/Citation
https://citeseerx.ist.psu.edu/viewdoc/citations?doi=10.1.1.695.2923