Exact GED: Difference between revisions
Jump to navigation
Jump to search
No edit summary |
No edit summary |
||
| Line 38: | Line 38: | ||
[[File:Graph Edit Distance Computation - Exact GED - Space.png|1000px]] | [[File:Graph Edit Distance Computation - Exact GED - Space.png|1000px]] | ||
== | == Space-Time Tradeoff Improvements == | ||
[[File:Graph Edit Distance Computation - Exact GED - Pareto Frontier.png|1000px]] | [[File:Graph Edit Distance Computation - Exact GED - Pareto Frontier.png|1000px]] | ||
Revision as of 14:37, 15 February 2023
Description
The GED of two graphs is defined as the minimum cost of an edit path between them, where an edit path is a sequence of edit operations (inserting, deleting, and relabeling vertices or edges) that transforms one graph into another. Exact GED computes the GED exactly.
Related Problems
Related: Inexact GED
Parameters
V: number of vertices in the larger of the two graphs
Table of Algorithms
| Name | Year | Time | Space | Approximation Factor | Model | Reference |
|---|---|---|---|---|---|---|
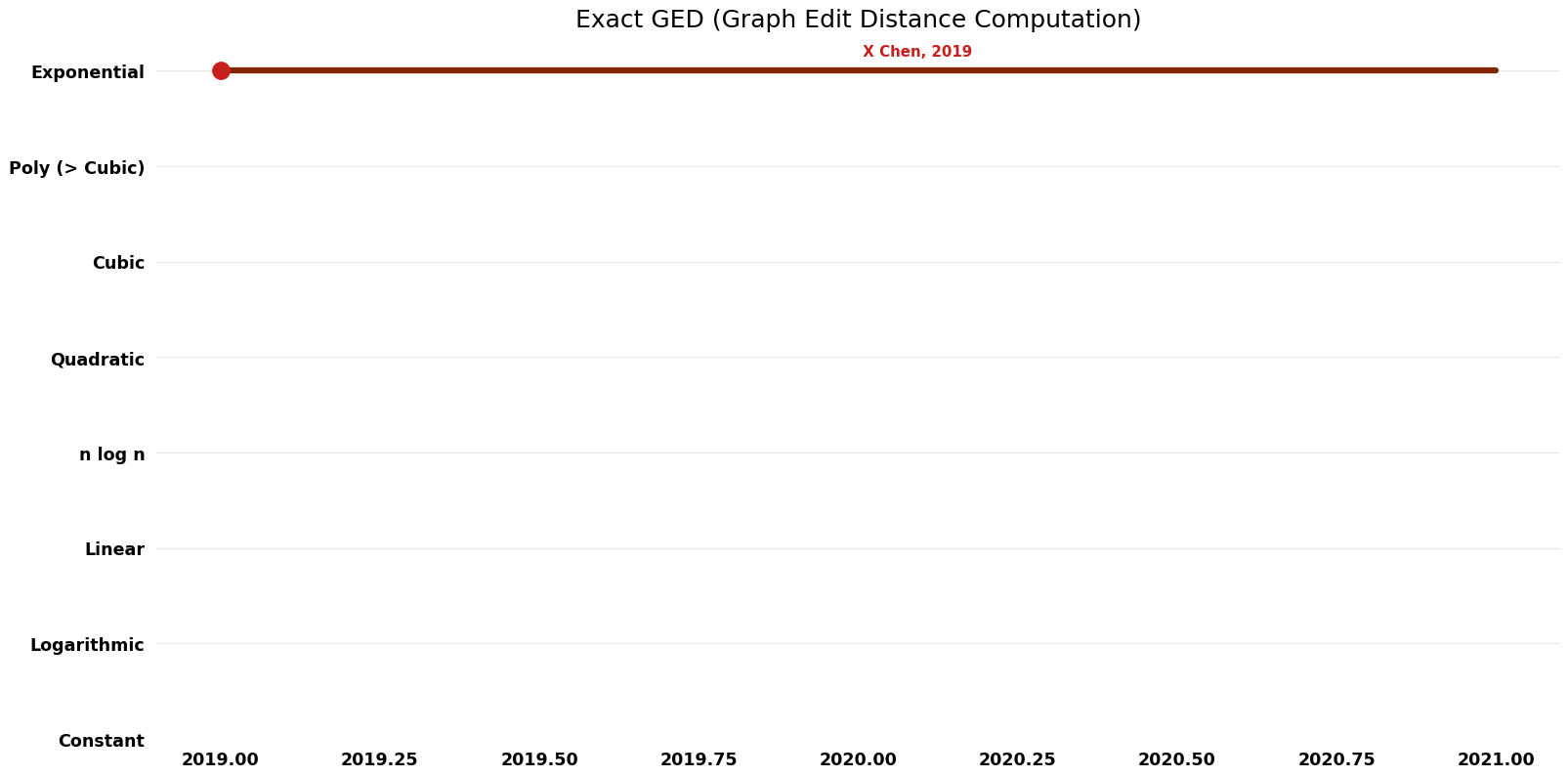
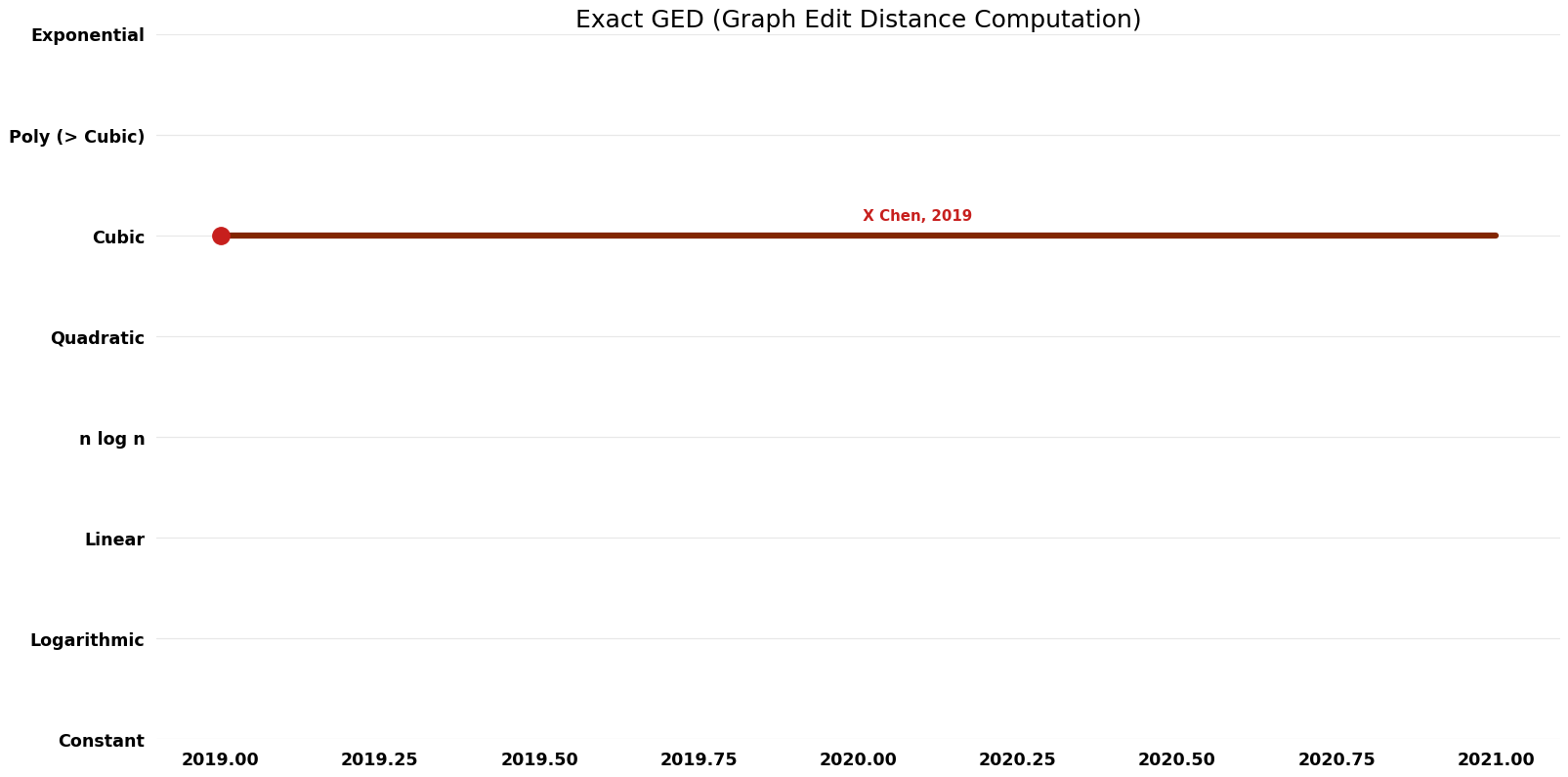
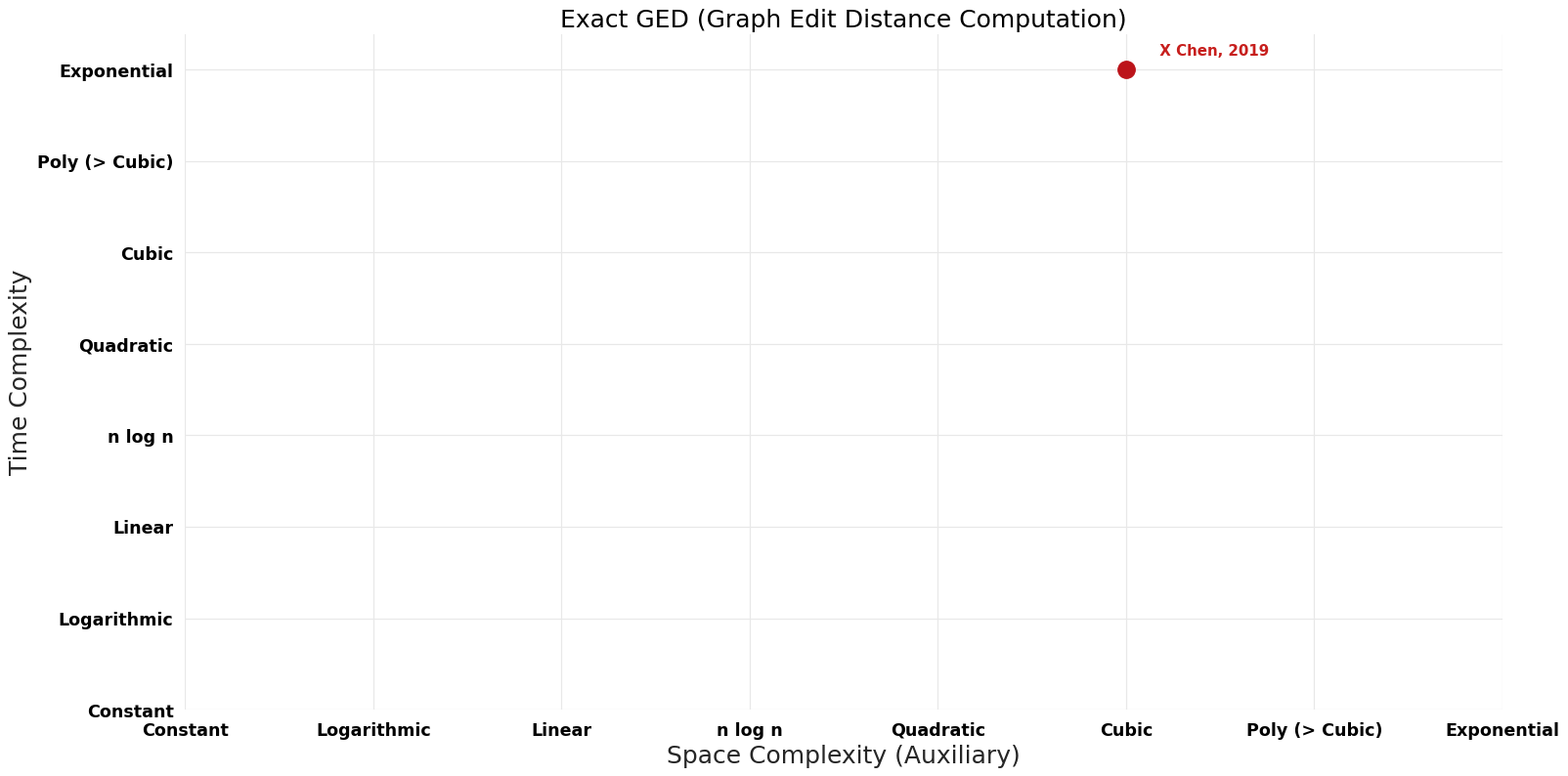
| X Chen | 2019 | $O(VS)$ | $O(wV^{2})$ | Exact | Deterministic | Time & Space |
| Alberto Sanfeliu and King-Sun Fu | 1983 | $O(V^{3} E^{2})$ | Exact | Deterministic | Time | |
| Wang Y-K; Fan K-C; Horng J-T | 1997 | $O(V E^{2} loglogE)$ | Exact | Deterministic | Time | |
| Tao D; Tang X; Li X et al | 2006 | $O(V^{2})$ | Exact | Deterministic | Time |
Time Complexity Graph
Space Complexity Graph
Space-Time Tradeoff Improvements
