Entity Resolution: Difference between revisions
Jump to navigation
Jump to search
(Created page with "{{DISPLAYTITLE:Entity Resolution (Entity Resolution)}} == Description == Entity resolution (ER) is the problem of matching records that represent the same real-world entity and then merging the matching records. ER is a well known problem that arises in many applications. An exhaustive ER process involves comparing all the pairs of records, which can be very expensive for large datasets. == Parameters == No parameters found. == Table of Algorithms == {| class="wi...") |
No edit summary |
||
| Line 34: | Line 34: | ||
|} | |} | ||
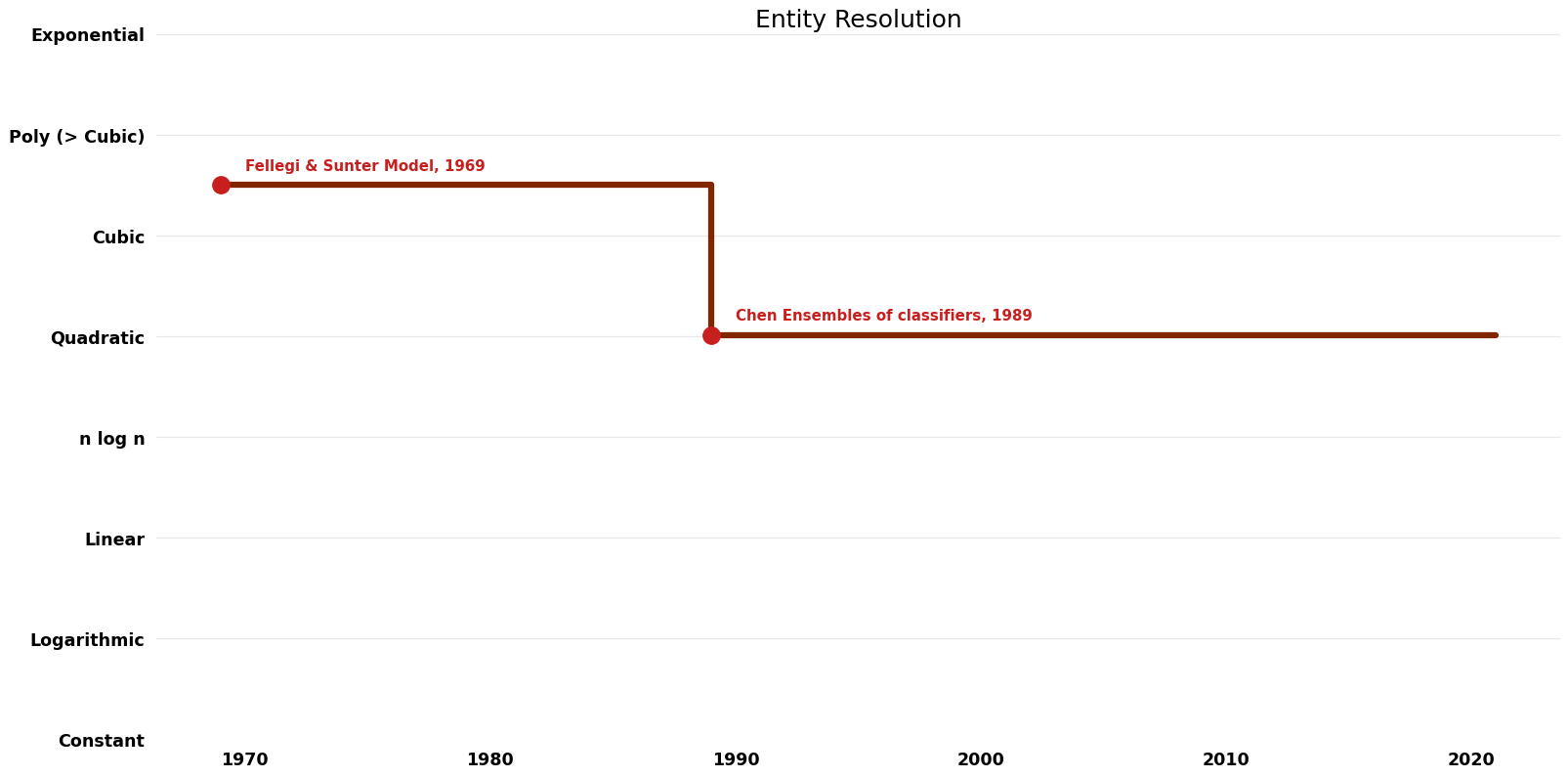
== Time Complexity | == Time Complexity Graph == | ||
[[File:Entity Resolution - Time.png|1000px]] | [[File:Entity Resolution - Time.png|1000px]] | ||
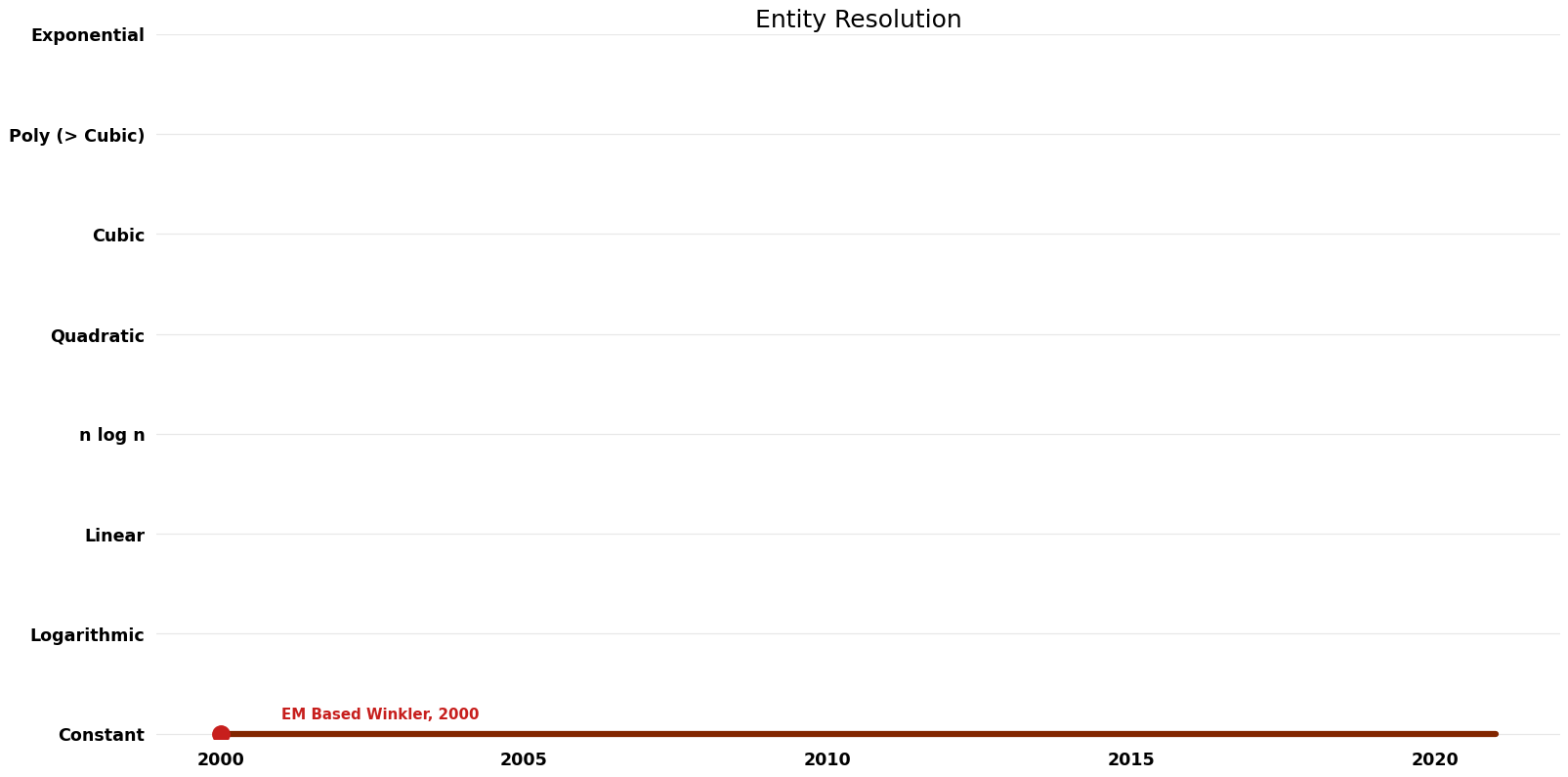
== Space Complexity | == Space Complexity Graph == | ||
[[File:Entity Resolution - Space.png|1000px]] | [[File:Entity Resolution - Space.png|1000px]] | ||
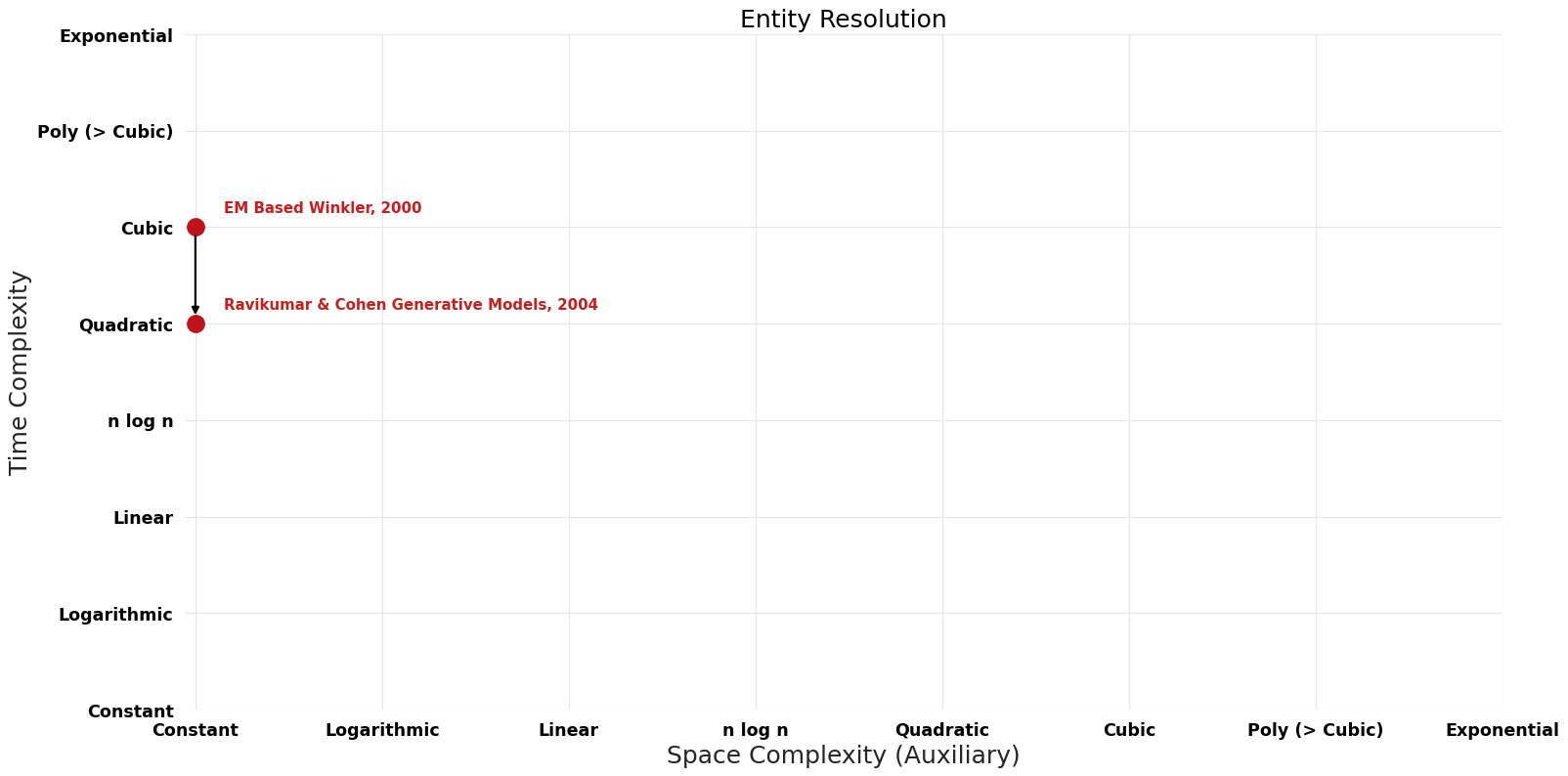
== Pareto | == Pareto Frontier Improvements Graph == | ||
[[File:Entity Resolution - Pareto Frontier.png|1000px]] | [[File:Entity Resolution - Pareto Frontier.png|1000px]] | ||
Revision as of 14:04, 15 February 2023
Description
Entity resolution (ER) is the problem of matching records that represent the same real-world entity and then merging the matching records. ER is a well known problem that arises in many applications. An exhaustive ER process involves comparing all the pairs of records, which can be very expensive for large datasets.
Parameters
No parameters found.
Table of Algorithms
| Name | Year | Time | Space | Approximation Factor | Model | Reference |
|---|---|---|---|---|---|---|
| Fellegi & Sunter Model | 1969 | $O(n^{3}k)$ | Exact | Deterministic | Time | |
| Gupta & Sarawagi CRF | 2009 | $O(n^{3}k)$ | Exact | Deterministic | Time | |
| Chen Ensembles of classifiers | 1989 | $O(n^{2} logn)$ | Exact | Deterministic | ||
| EM Based Winkler | 2000 | $O(n^{3}k)$ | $O(k)$ | Exact | Deterministic | Time |
| Ravikumar & Cohen Generative Models | 2004 | $O(n^{2} k)$ | $O(k)$ | Exact | Deterministic | Time |
| Bellare Active Learning | 2012 | $O(n^{2} logn clogc)$ | Exact | Deterministic | Time | |
| Ananthakrishna | 2002 | $O(n^{2} k)$ | $O(n)$ | Exact | Deterministic | Time |
| Record linking | 1993 | $O(n^{2}k)$ | Exact | Deterministic |