Gröbner Bases: Difference between revisions
Jump to navigation
Jump to search
No edit summary |
No edit summary |
||
| Line 26: | Line 26: | ||
|} | |} | ||
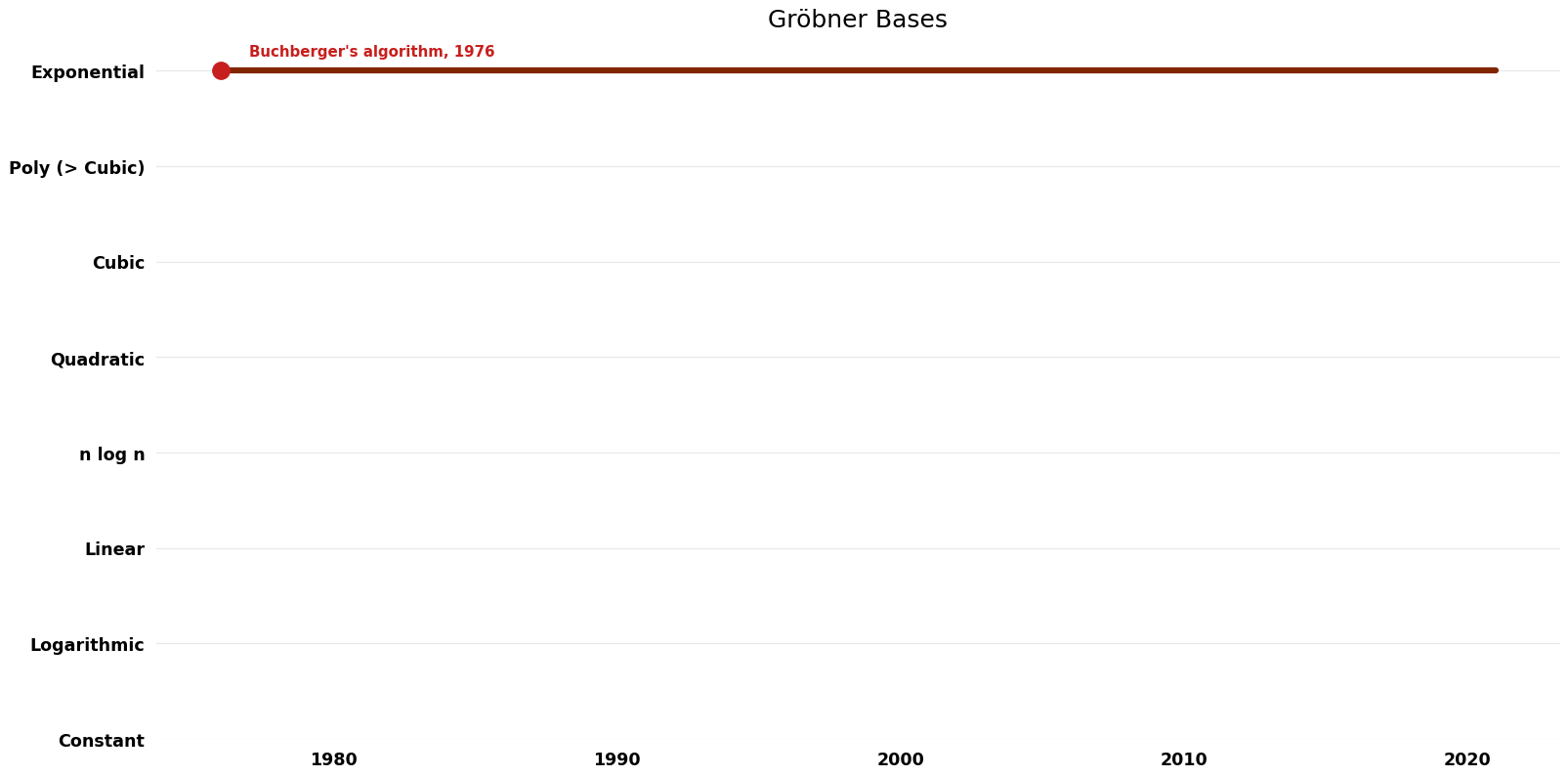
== Time Complexity | == Time Complexity Graph == | ||
[[File:Gröbner Bases - Time.png|1000px]] | [[File:Gröbner Bases - Time.png|1000px]] | ||
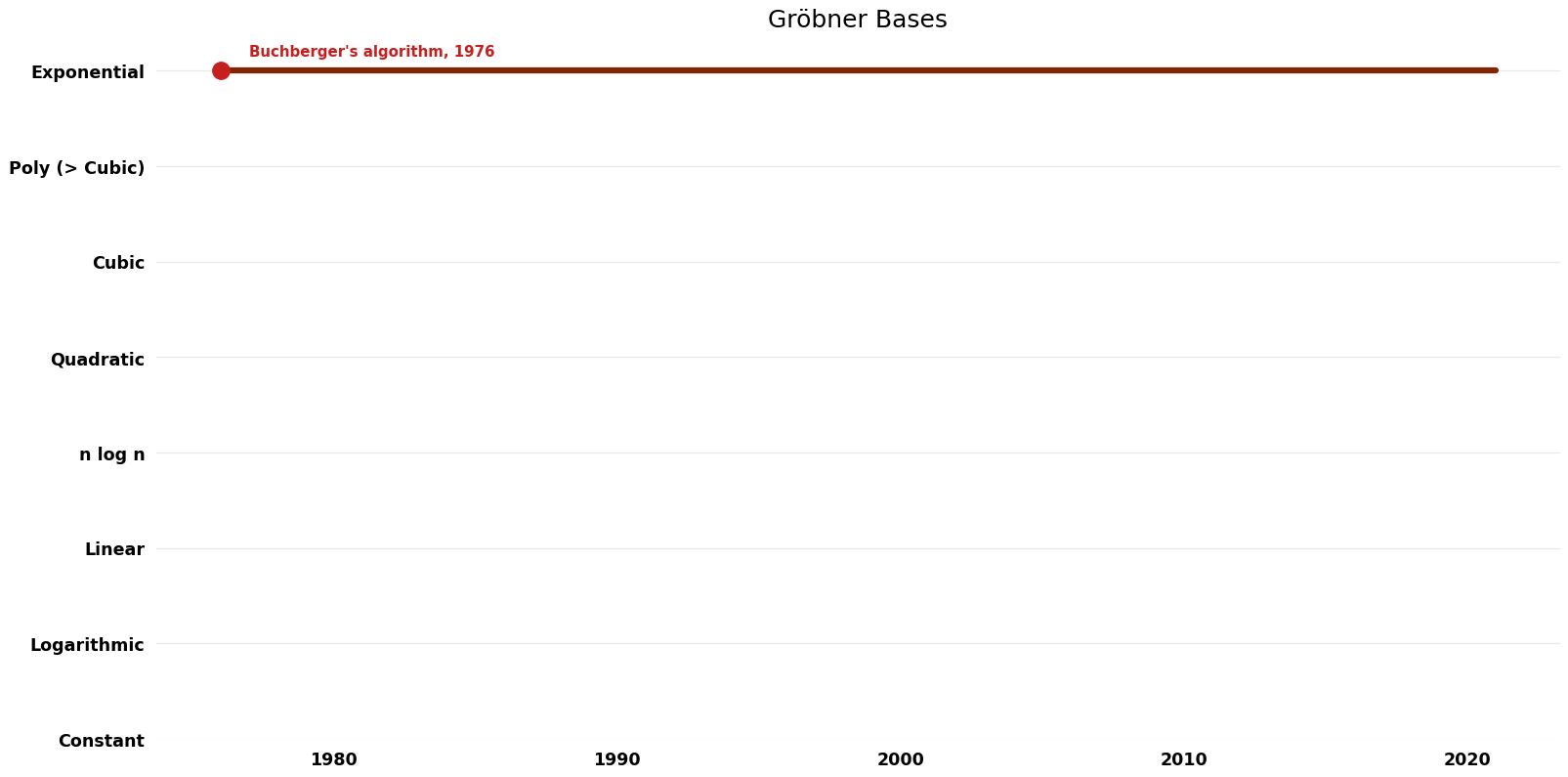
== Space Complexity | == Space Complexity Graph == | ||
[[File:Gröbner Bases - Space.png|1000px]] | [[File:Gröbner Bases - Space.png|1000px]] | ||
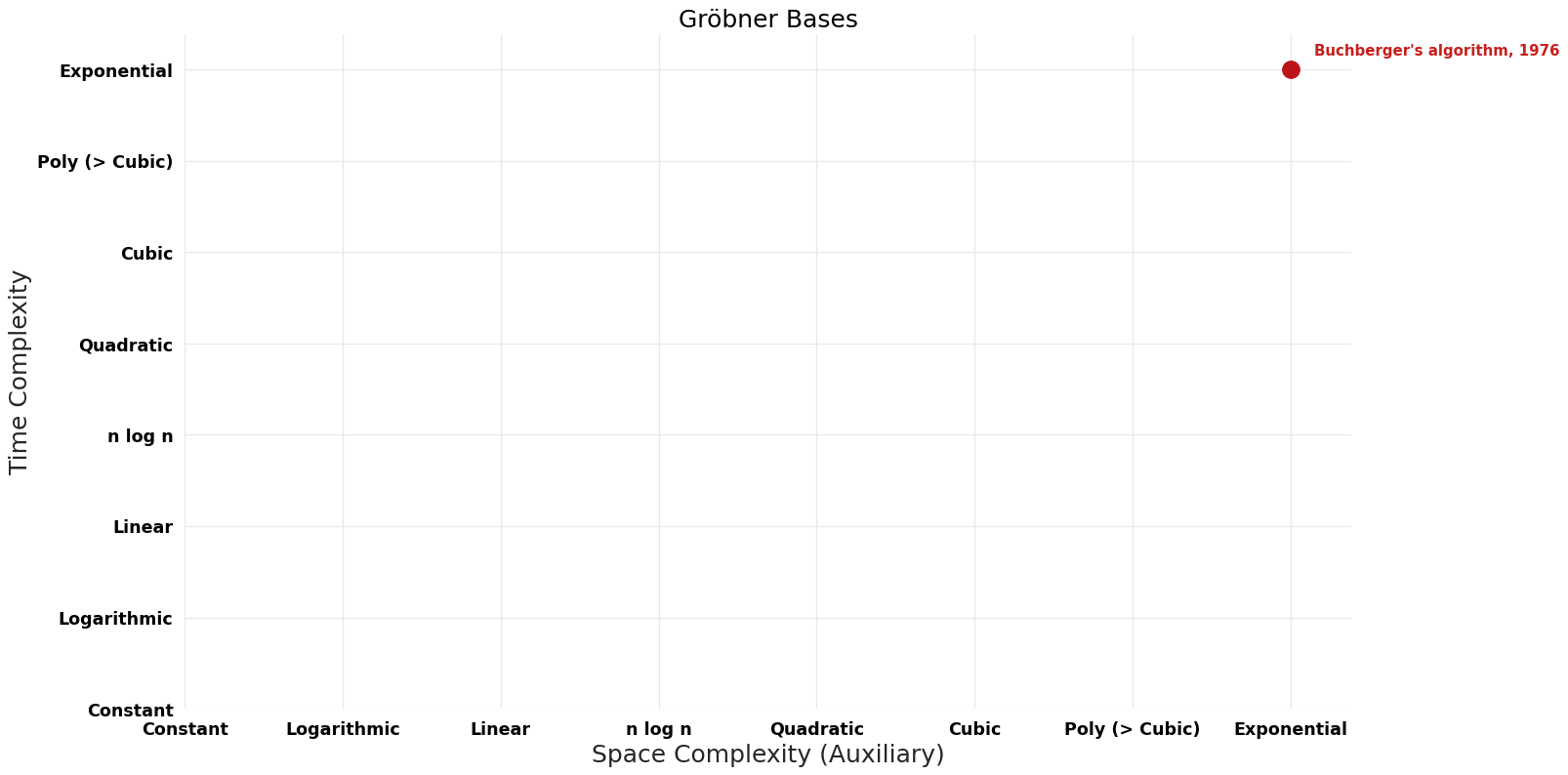
== Pareto | == Pareto Frontier Improvements Graph == | ||
[[File:Gröbner Bases - Pareto Frontier.png|1000px]] | [[File:Gröbner Bases - Pareto Frontier.png|1000px]] | ||
Revision as of 14:04, 15 February 2023
Description
In mathematics, and more specifically in computer algebra, computational algebraic geometry, and computational commutative algebra, a Gröbner basis is a particular kind of generating set of an ideal in a polynomial ring $K(x_1, \ldots ,x_n)$ over a field $K$. As an algorithmic problem, given a set of polynomials in $K(x_1, \ldots,x_n)$, determine a Gröbner basis.
Parameters
n: number of variables in each polynomial
d: maximal total degree of the polynomials
Table of Algorithms
| Name | Year | Time | Space | Approximation Factor | Model | Reference |
|---|---|---|---|---|---|---|
| Buchberger's algorithm | 1976 | d^{({2}^{(n+o({1})})}) | d^{({2}^{(n+o({1}))})}?? | Exact | Deterministic | Time |
| Faugère F4 algorithm | 1999 | $O(C(n+D_reg, D_reg)$^{\omega}) where omega is the exponent on matrix multiplication | $O(C(n+D_{reg}, D_{reg})$^{2})? | Exact | Deterministic | Time |
| Faugère F5 algorithm | 2002 | $O(C(n+D_reg, D_reg)$^{\omega}) where omega is the exponent on matrix multiplication | $O(C(n+D_{reg}, D_{reg})$^{2})? | Exact | Deterministic | Time |