St-Maximum Flow: Difference between revisions
Jump to navigation
Jump to search
No edit summary |
No edit summary |
||
| Line 84: | Line 84: | ||
|} | |} | ||
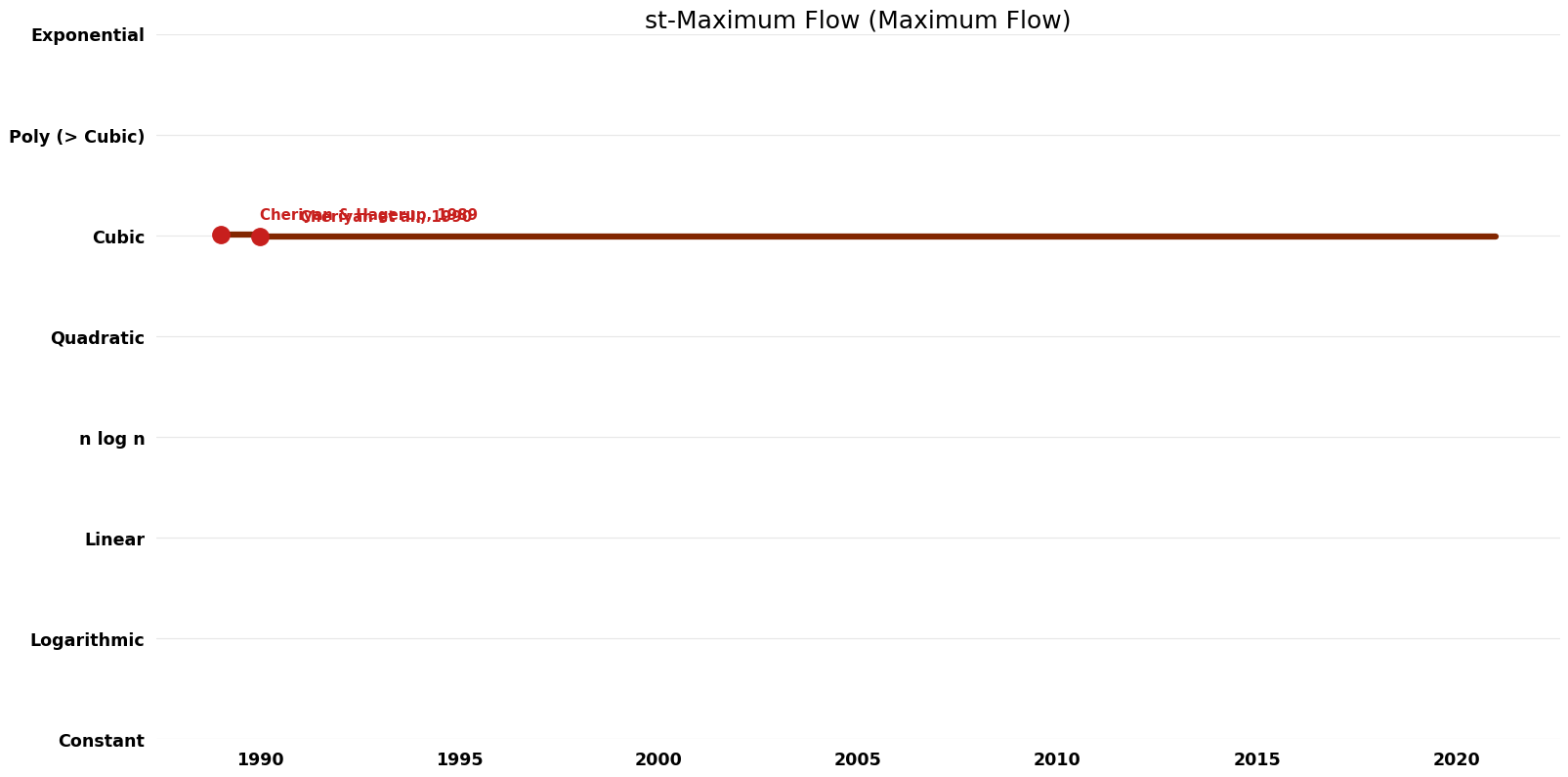
== Time Complexity | == Time Complexity Graph == | ||
[[File:Maximum Flow - st-Maximum Flow - Time.png|1000px]] | [[File:Maximum Flow - st-Maximum Flow - Time.png|1000px]] | ||
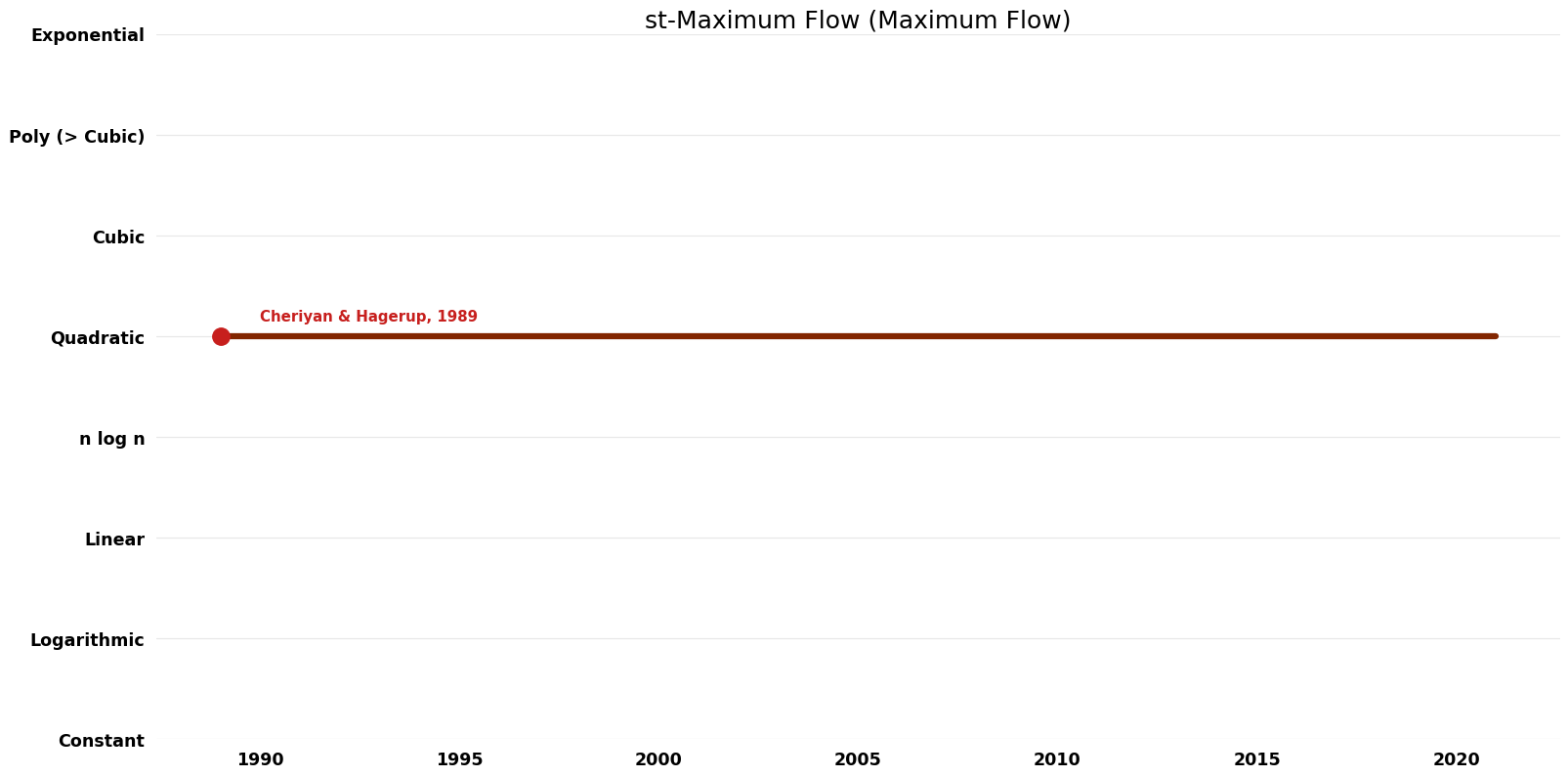
== Space Complexity | == Space Complexity Graph == | ||
[[File:Maximum Flow - st-Maximum Flow - Space.png|1000px]] | [[File:Maximum Flow - st-Maximum Flow - Space.png|1000px]] | ||
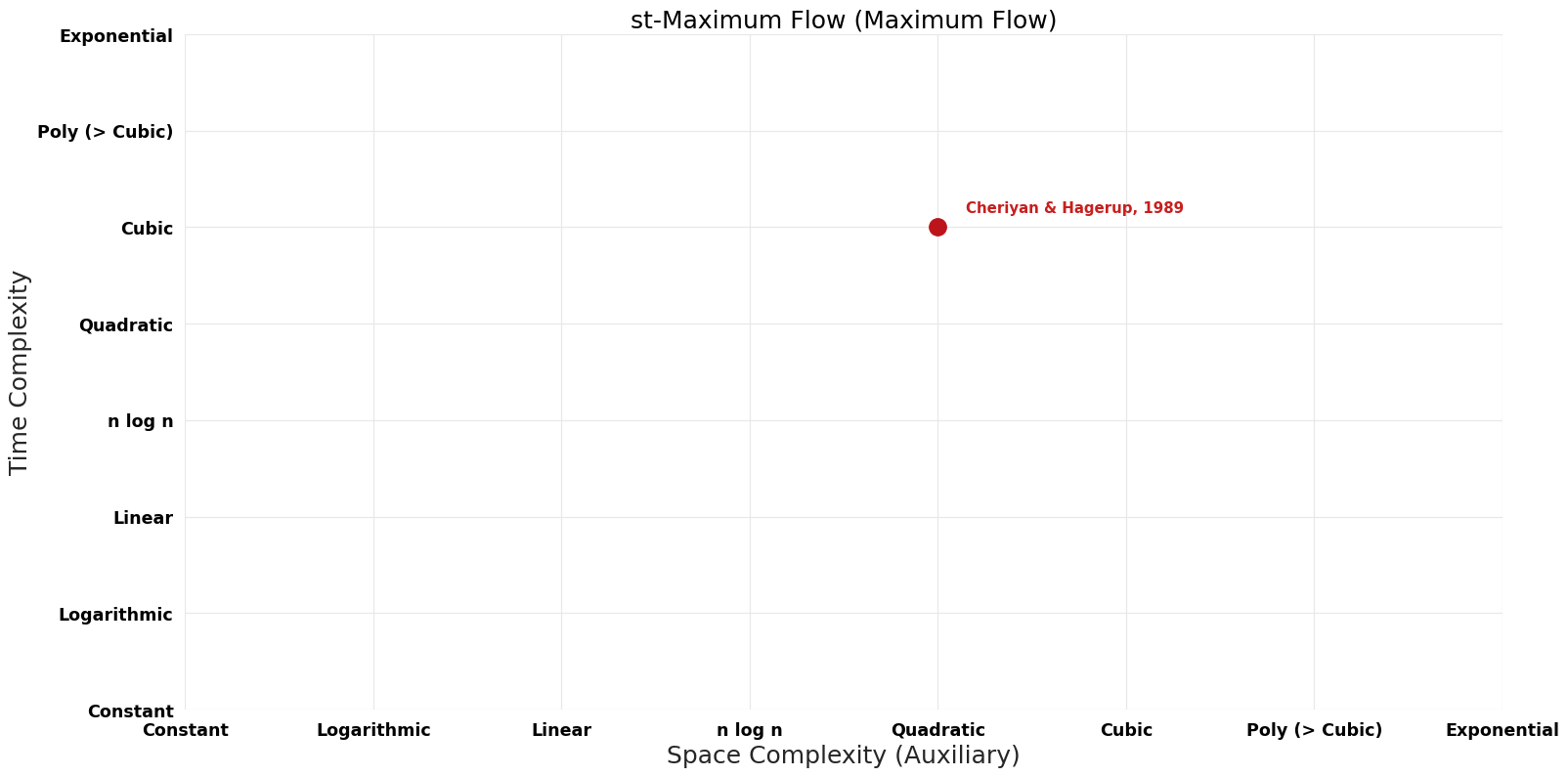
== Pareto | == Pareto Frontier Improvements Graph == | ||
[[File:Maximum Flow - st-Maximum Flow - Pareto Frontier.png|1000px]] | [[File:Maximum Flow - st-Maximum Flow - Pareto Frontier.png|1000px]] | ||
Revision as of 14:03, 15 February 2023
Description
Find the maximum flow from $s$ to $t$
Related Problems
Related: Integer Maximum Flow, Unweighted Maximum Flow, Non-integer Maximum Flow, Minimum-Cost Flow, All-Pairs Maximum Flow, Maximum Local Edge Connectivity
Parameters
V: number of vertices
E: number of edges
U: maximum edge capacity
Table of Algorithms
| Name | Year | Time | Space | Approximation Factor | Model | Reference |
|---|---|---|---|---|---|---|
| Ford & Fulkerson | 1955 | $O(E^{2}U)$ | $O(E)$ | Exact | Deterministic | Time & Space |
| Dinitz | 1970 | $O(V^{2}E)$ | $O(E)$ | Exact | Deterministic | Time & Space |
| Edmonds & Karp | 1972 | $O(E^{2}LogU)$ | $O(E)$ | Exact | Deterministic | Time & Space |
| Karzanov | 1974 | $O(V^{3})$ | $O(V^{2})$ | Exact | Deterministic | Time & Space |
| Galil & Naamad | 1980 | $O(VELog^{2}V)$ | $O(E)$ | Exact | Deterministic | Time & Space |
| Dantzig | 1951 | $O(V^{2}EU)$ | $O(VE)$? | Exact | Deterministic | |
| Dinitz (with dynamic trees) | 1973 | $O(VELogU)$ | $O(E)$ | Exact | Deterministic | Time |
| Cherkassky | 1977 | $O(V^{2}E^{0.5})$ | $O(E)$ | Exact | Deterministic | Time & Space |
| Sleator & Tarjan | 1983 | $O(VELogV)$ | $O(E)$ | Exact | Deterministic | Time |
| Goldberg & Tarjan | 1986 | $O(VELog(V^{2}/E))$ | $O(E)$ | Exact | Deterministic | Time |
| Ahuja & Orlin | 1987 | $O(VE + V^{2}LogU)$ | $O(ELogU)$ | Exact | Deterministic | Time |
| Cheriyan & Hagerup | 1989 | $O(VE*log(V))$ | $O(V + E)$ | Exact | Randomized | Time |
| Cheriyan et al. | 1990 | $O(V^{3} / LogV)$ | $O(V + E)$ | Exact | Deterministic | Time |
| Alon | 1990 | $O(VE + V^{({2.66})}LogV)$ | $O(V + E)$ | Exact | Deterministic | Time |
| King et al. (KRT) | 1992 | $O(VE + V^{({2}+eps)})$ | $O(V + E)$ | Exact | Deterministic | Time |
| Phillips & Westbrook | 1993 | $O(VE(Log(V;V/E)) + V^{2}(LogV)^{2} )$ | $O(V + E)$ | Exact | Deterministic | Time |
| James B Orlin's + KRT (King; Rao; Tarjan)'s algorithm | 2013 | $O(VE)$ | $O(V + E)$ | Exact | Deterministic | Time |
| Ahuja et al. | 1987 | $O(VELog(V(LogU)$^{0.5} / E)) | Exact | Deterministic | Time | |
| MKM Algorithm | 1978 | $O(V^{3})$ | $O(E)$ | Exact | Deterministic | Time & Space |
| Galil | 1978 | $O(V^({5}/{3})$E^({2}/{3})) | $O(E)$ | Exact | Deterministic | Time & Space |
| Shiloach | 1981 | $O(V^{3}*log(V)$/p) | $O(E)$ | Exact | Parallel | Time |
| Gabow | 1985 | $O(VE*logU)$ | $O(E)$ | Exact | Deterministic | Time |
| Lee, Sidford | 2014 | $O(E*sqrt(V)$*log^{2}(U)*polylog(E, V, log(U)) | $O(E)$ | Exact | Deterministic | Time |
| Madry | 2016 | $O(E^({10}/{7})$U^({1}/{7})polylog(V, E, log U)) | $O(E)$ | Exact | Deterministic | Time |
| Kathuria, Liu, Sidford | 2020 | $O(E^({1}+o({1})$)/sqrt(eps)) | $O(E)$ or $O(V^{2})$ ? | 1+eps | Deterministic | Time |
| Kathuria, Liu, Sidford | 2020 | $O(E^({4}/{3}+o({1})$)U^({1}/{3})) | $O(E)$ or $O(V^{2})$ ? | Exact | Deterministic | Time |
| Brand et al | 2021 | $O((E+V^{1.5})$log(U)polylog(V, E, log U)) | $O(E)$ | Exact | Randomized | Time |
| Gao, Liu, Peng | 2021 | $O(E^({3}/{2}-{1}/{328})$*log(U)*polylog(E)) | $O(E)$ | Exact | Deterministic | Time |
| Chen et al | 2022 | $O(E^({1}+o({1})$)*log(U)) | $O(E)$ | Exact | Deterministic | Time |
Time Complexity Graph
Space Complexity Graph
Pareto Frontier Improvements Graph
Reductions FROM Problem
| Problem | Implication | Year | Citation | Reduction |
|---|---|---|---|---|
| MAX-CNF-SAT | assume: SETH then: for any fixed constants $\epsilon > {0}$, $c_1,c_2 \in ({0},{1})$, on graphs with $n$ nodes $|S|=\tilde{\Theta}(n^{c_1})$, $|T|=\tilde{\Theta(n^{c_2})}$, $m=O(n)$ edges, and capacaties in $\{1,\cdots,n\}$, target cannot be solved in $O((|S|T|m)^{1-\epsilon})$ |
2018 | https://dl.acm.org/doi/abs/10.1145/3212510 | link |
| MAX-CNF-SAT | assume: SETH then: for any fixed $\epsilon > {0}$, in graphs with $n$ nodes, $m=O(n)$ edges, and capacities in $\{1,\cdots,n\}$ target cannot be solved in time $O((n^{2}m)^{1-\epsilon})$ |
2018 | https://dl.acm.org/doi/abs/10.1145/3212510 | link |