Kth Order Statistic: Difference between revisions
Jump to navigation
Jump to search
(Created page with "{{DISPLAYTITLE:kth Order Statistic (kth Order Statistic)}} == Description == An algorithm seeks to find the $k^{th}$ order statistic of a statistical sample, or the $k^{th}$-smallest value in a list or array. == Parameters == <pre>n: size of list</pre> == Table of Algorithms == {| class="wikitable sortable" style="text-align:center;" width="100%" ! Name !! Year !! Time !! Space !! Approximation Factor !! Model !! Reference |- | Naive Selection (kth Order St...") |
No edit summary |
||
| Line 6: | Line 6: | ||
== Parameters == | == Parameters == | ||
n: size of list | |||
== Table of Algorithms == | == Table of Algorithms == | ||
| Line 24: | Line 24: | ||
|} | |} | ||
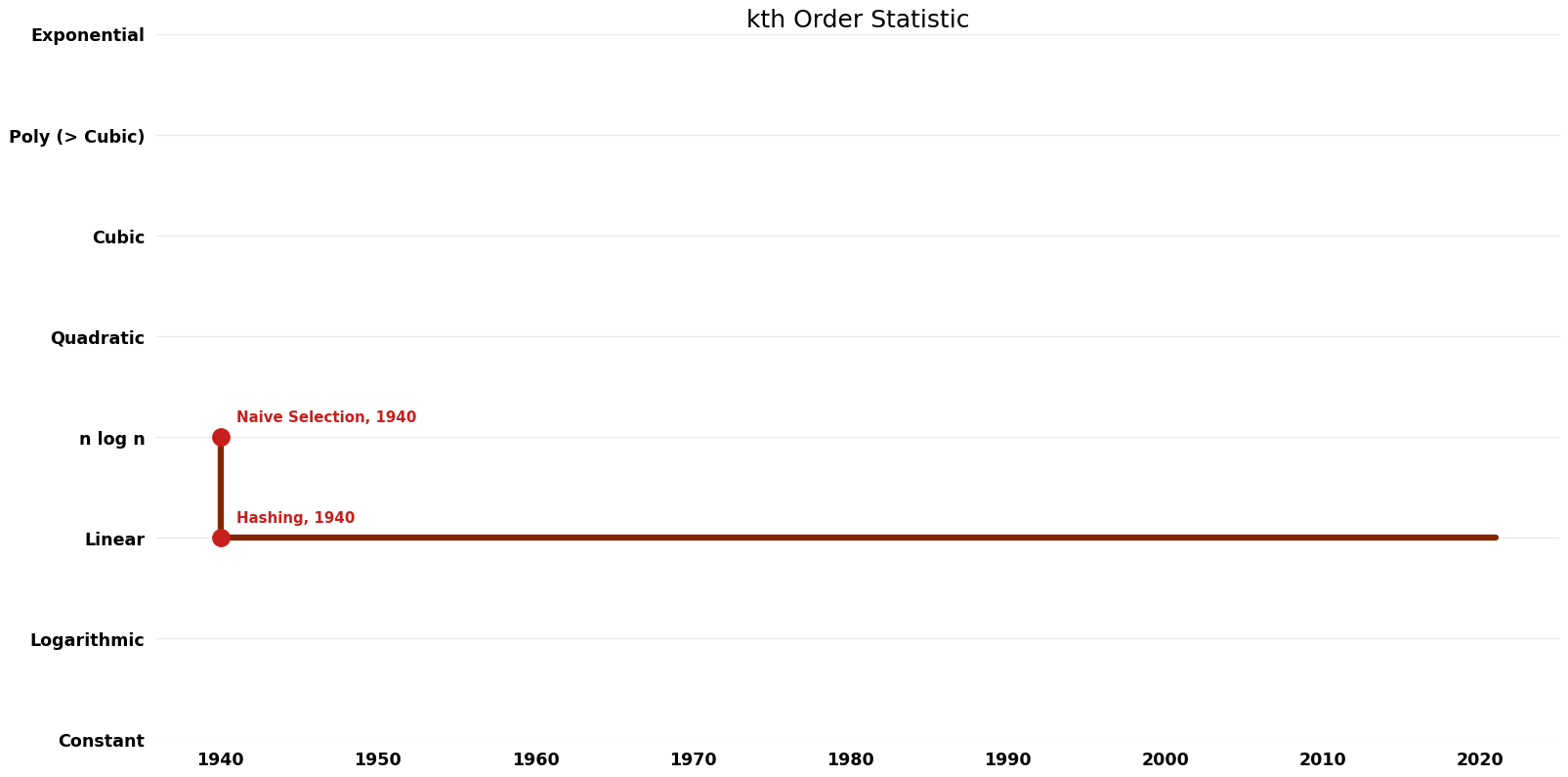
== Time Complexity | == Time Complexity Graph == | ||
[[File:kth Order Statistic - Time.png|1000px]] | [[File:kth Order Statistic - Time.png|1000px]] | ||
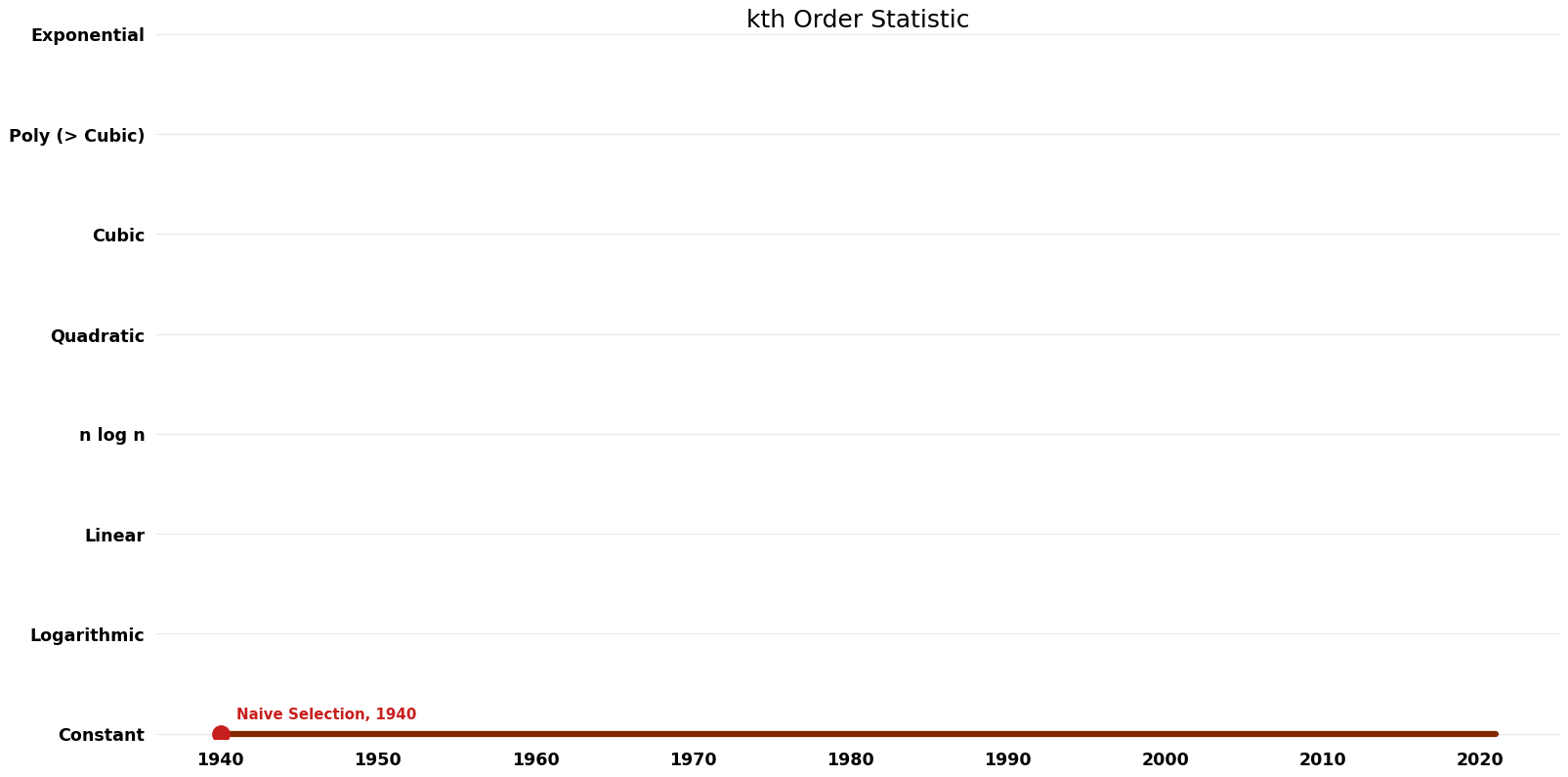
== Space Complexity | == Space Complexity Graph == | ||
[[File:kth Order Statistic - Space.png|1000px]] | [[File:kth Order Statistic - Space.png|1000px]] | ||
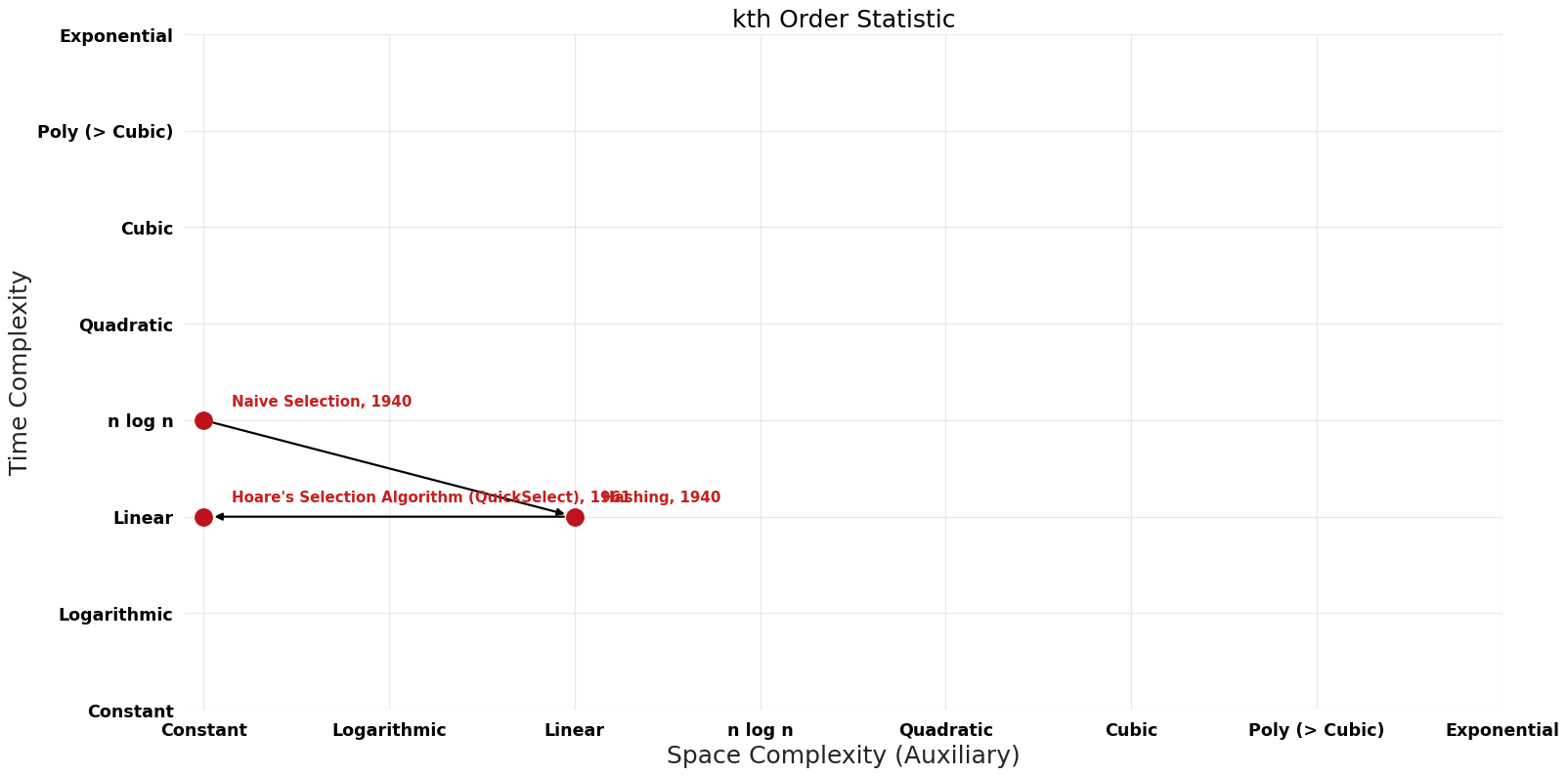
== Pareto | == Pareto Frontier Improvements Graph == | ||
[[File:kth Order Statistic - Pareto Frontier.png|1000px]] | [[File:kth Order Statistic - Pareto Frontier.png|1000px]] | ||
Revision as of 14:03, 15 February 2023
Description
An algorithm seeks to find the $k^{th}$ order statistic of a statistical sample, or the $k^{th}$-smallest value in a list or array.
Parameters
n: size of list
Table of Algorithms
| Name | Year | Time | Space | Approximation Factor | Model | Reference |
|---|---|---|---|---|---|---|
| Naive Selection | 1940 | $O(nlogn)$ | $O({1})$ (can use in-situ sorting) | Exact | Deterministic | |
| Hoare's Selection Algorithm (QuickSelect) | 1961 | $O(n)$ | $O({1})$ (in-situ) | Exact | Deterministic | Time |
| Hashing | 1940 | $O(n)$ | $O(n)$ | Exact | Deterministic |
Time Complexity Graph
Space Complexity Graph
Pareto Frontier Improvements Graph
References/Citation
https://11011110.github.io/blog/2007/10/09/blum-style-analysis-of.html