CFG Recognition: Difference between revisions
Jump to navigation
Jump to search
(Created page with "{{DISPLAYTITLE:CFG Recognition (CFG Problems)}} == Description == Given a grammar $G$ and a string $s$, determine if the string $s$ can be derived by the grammar $G$. == Related Problems == Related: CFG Parsing == Parameters == <pre>n: length of the given string</pre> == Table of Algorithms == {| class="wikitable sortable" style="text-align:center;" width="100%" ! Name !! Year !! Time !! Space !! Approximation Factor !! Model !! Reference |- | Cocke...") |
No edit summary |
||
| Line 10: | Line 10: | ||
== Parameters == | == Parameters == | ||
n: length of the given string | |||
== Table of Algorithms == | == Table of Algorithms == | ||
Revision as of 13:03, 15 February 2023
Description
Given a grammar $G$ and a string $s$, determine if the string $s$ can be derived by the grammar $G$.
Related Problems
Related: CFG Parsing
Parameters
n: length of the given string
Table of Algorithms
| Name | Year | Time | Space | Approximation Factor | Model | Reference |
|---|---|---|---|---|---|---|
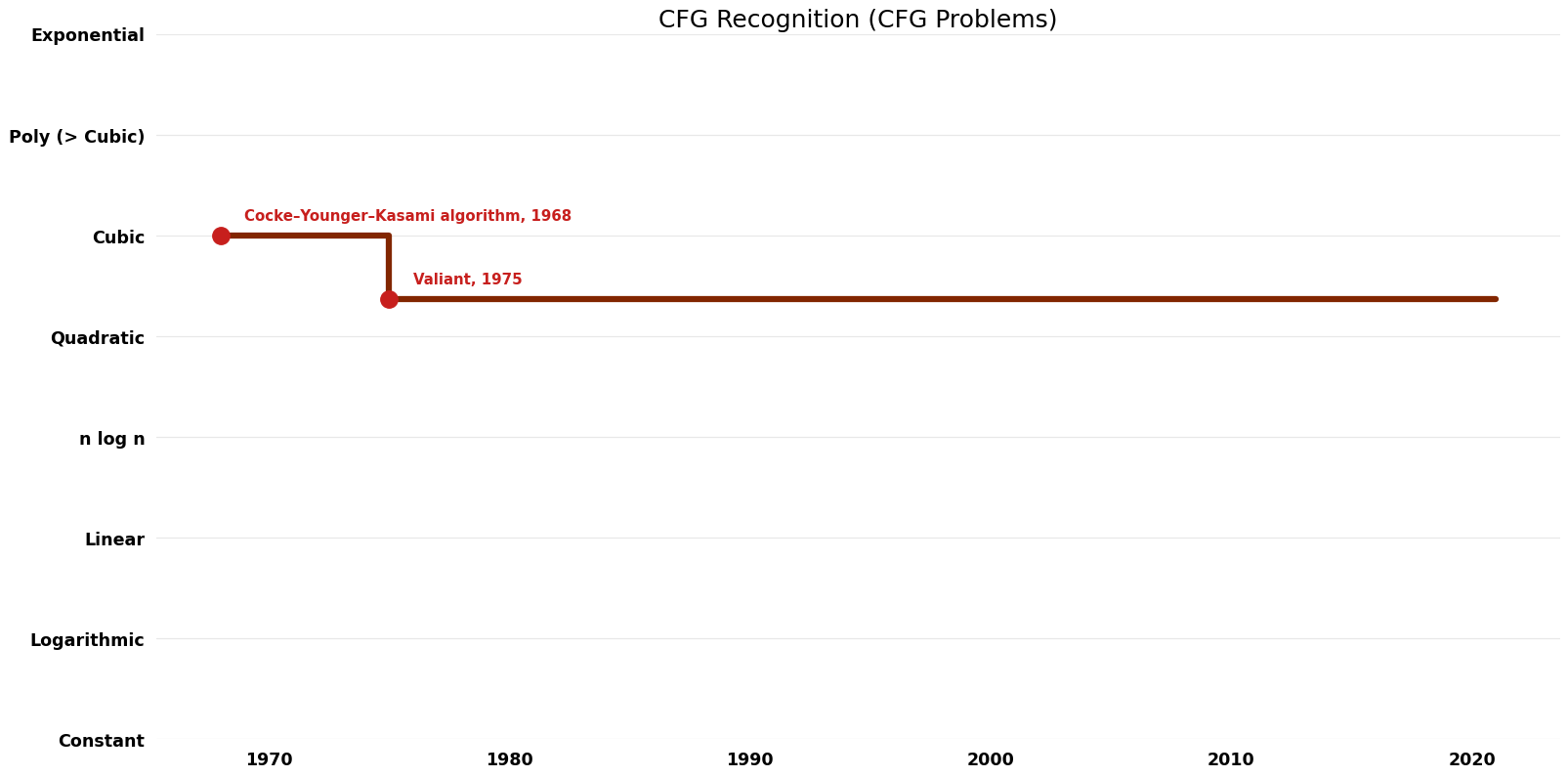
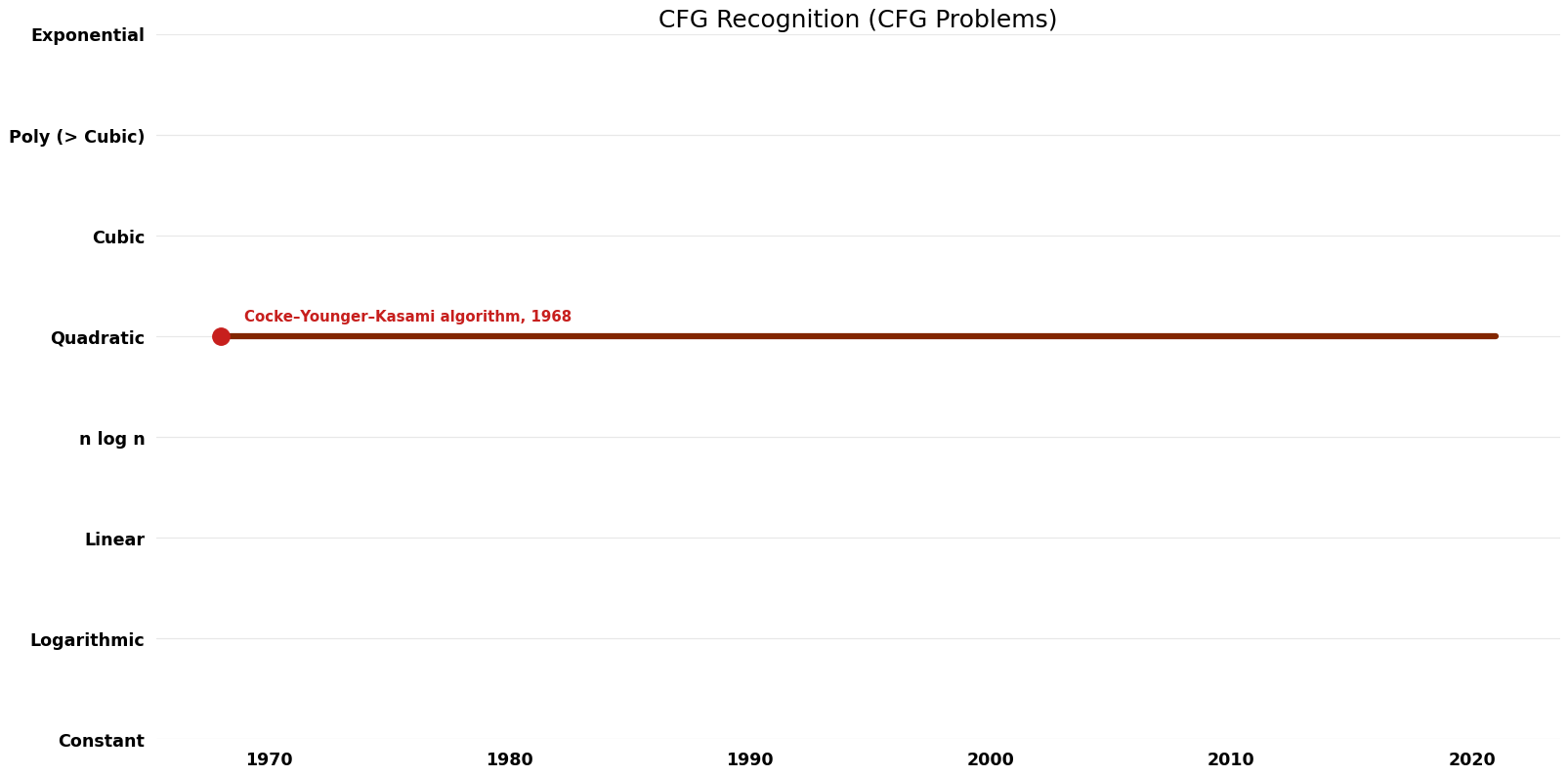
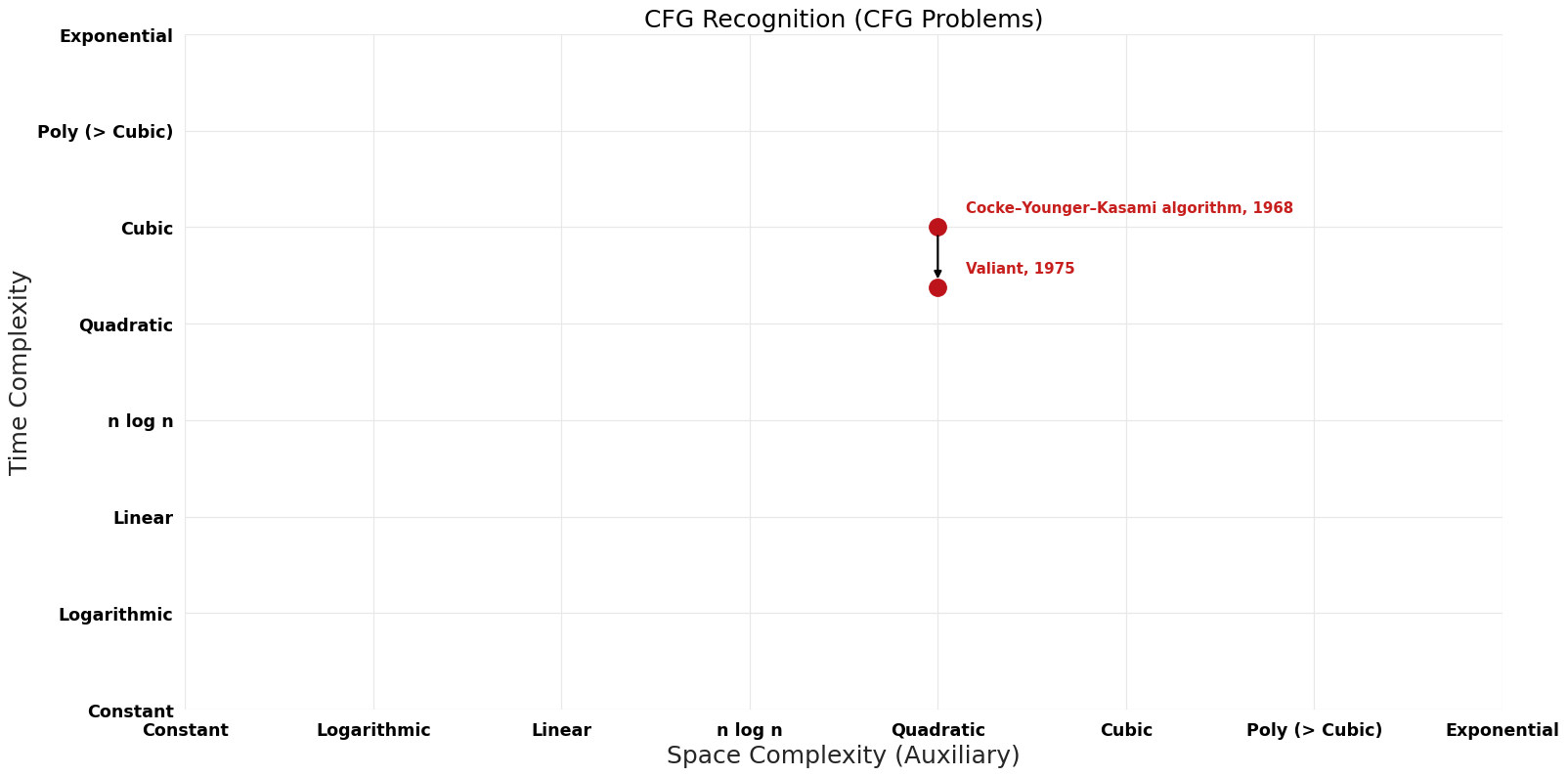
| Cocke–Younger–Kasami algorithm | 1968 | G|)$ | $O(n^{2})$ | Exact | Deterministic | Time & Space |
| Valiant | 1975 | G|)$ where omega is the exponent for matrix multiplication | $O(n^{2})$? | Exact | Deterministic | Time |
Time Complexity graph
Space Complexity graph
Pareto Decades graph
Reductions FROM Problem
| Problem | Implication | Year | Citation | Reduction |
|---|---|---|---|---|
| k-Clique | assume: k-Clique Hypothesis then: there is no $O(N^{\omega-\epsilon}) time algorithm for target for any $\epsilon > {0}$ |
2017 | https://ieeexplore.ieee.org/abstract/document/8104058 | link |
| k-Clique | assume: k-Clique Hypothesis then: there is no $O(N^{\{3}-\epsilon}) time combinatorial algorithm for target for any $\epsilon > {0}$ |
2017 | https://ieeexplore.ieee.org/abstract/document/8104058 | link |
References/Citation
https://linkinghub.elsevier.com/retrieve/pii/S0022000075800468