Delaunay Triangulation: Difference between revisions
Jump to navigation
Jump to search
(Created page with "{{DISPLAYTITLE:Delaunay Triangulation (Delaunay Triangulation)}} == Description == Given a set of points, the Delaunay Triangulation problem is to triangulate the points using the following notion of triangulation. $AB$ is an edge of the Delaunay triangulation iff there is a circle passing through $A$ and $B$ so that all other points in the point set, $C$, where $C$ is not equal to $A$ or $B$, lie outside the circle. Equivalently, all triangles in the Delaunay triangu...") |
No edit summary |
||
| Line 8: | Line 8: | ||
== Parameters == | == Parameters == | ||
n: number of points | |||
== Table of Algorithms == | == Table of Algorithms == | ||
Revision as of 12:03, 15 February 2023
Description
Given a set of points, the Delaunay Triangulation problem is to triangulate the points using the following notion of triangulation.
$AB$ is an edge of the Delaunay triangulation iff there is a circle passing through $A$ and $B$ so that all other points in the point set, $C$, where $C$ is not equal to $A$ or $B$, lie outside the circle. Equivalently, all triangles in the Delaunay triangulation for a set of points will have empty circumscribed circles. That is, no points lie in the interior of any triangle's circumcircle.
Parameters
n: number of points
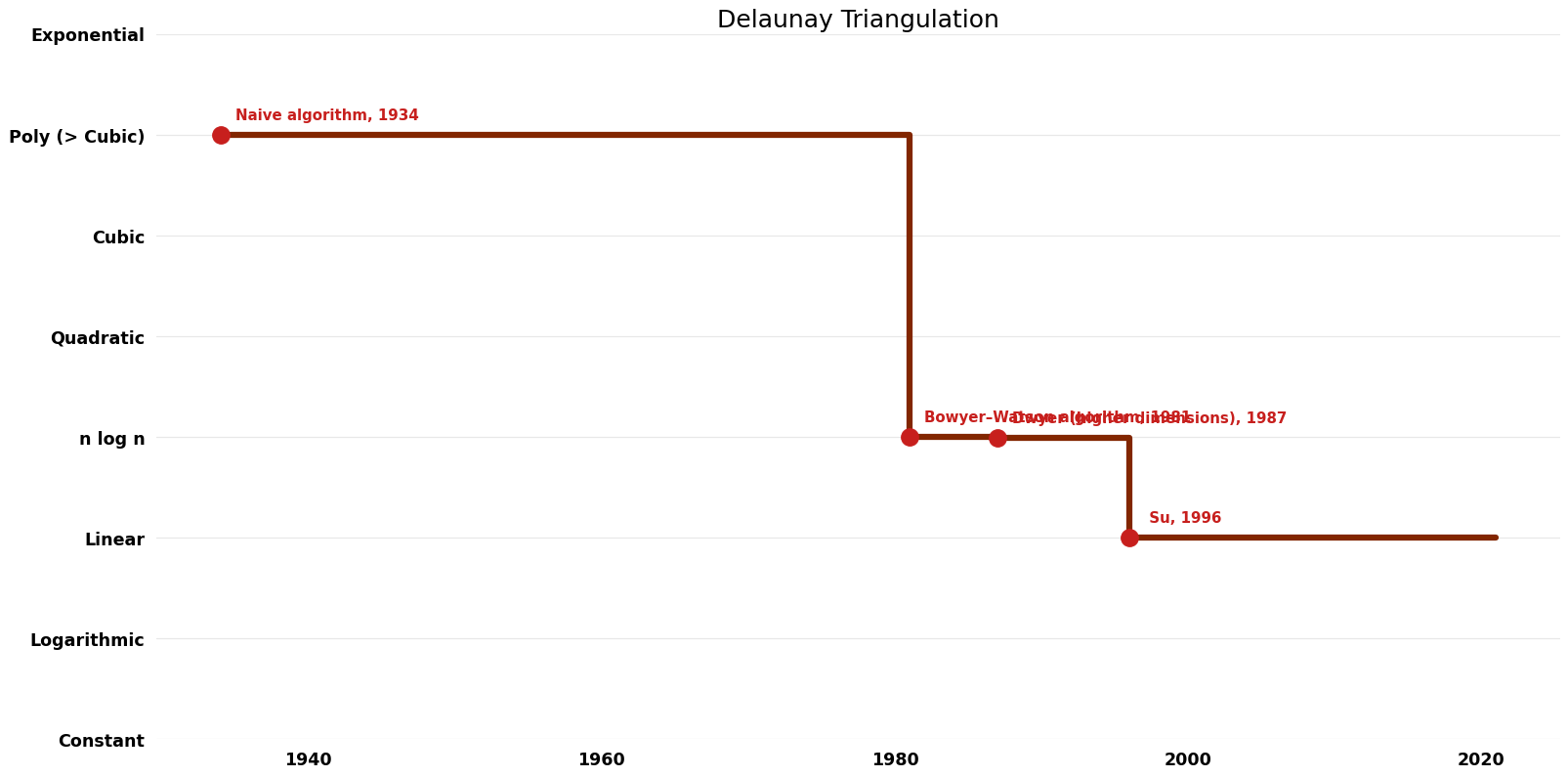
Table of Algorithms
| Name | Year | Time | Space | Approximation Factor | Model | Reference |
|---|---|---|---|---|---|---|
| Katajainen and M. Koppinen | 1987 | $O(n log log n)$ | Exact | Deterministic | Time |
Time Complexity graph
Space Complexity graph
Pareto Decades graph
