Enumerating Maximal Cliques, arbitrary graph

Description

A maximal clique (complete subgraph) is a clique that is not contained in any other clique. The goal here is to enumerate such maximal cliques in a given graph.

Related Problems

Related: k-Clique, Exact k-Clique, Min-Weight k-Clique, Max-Weight k-Clique

Parameters

n: number of vertices

m: number of edges

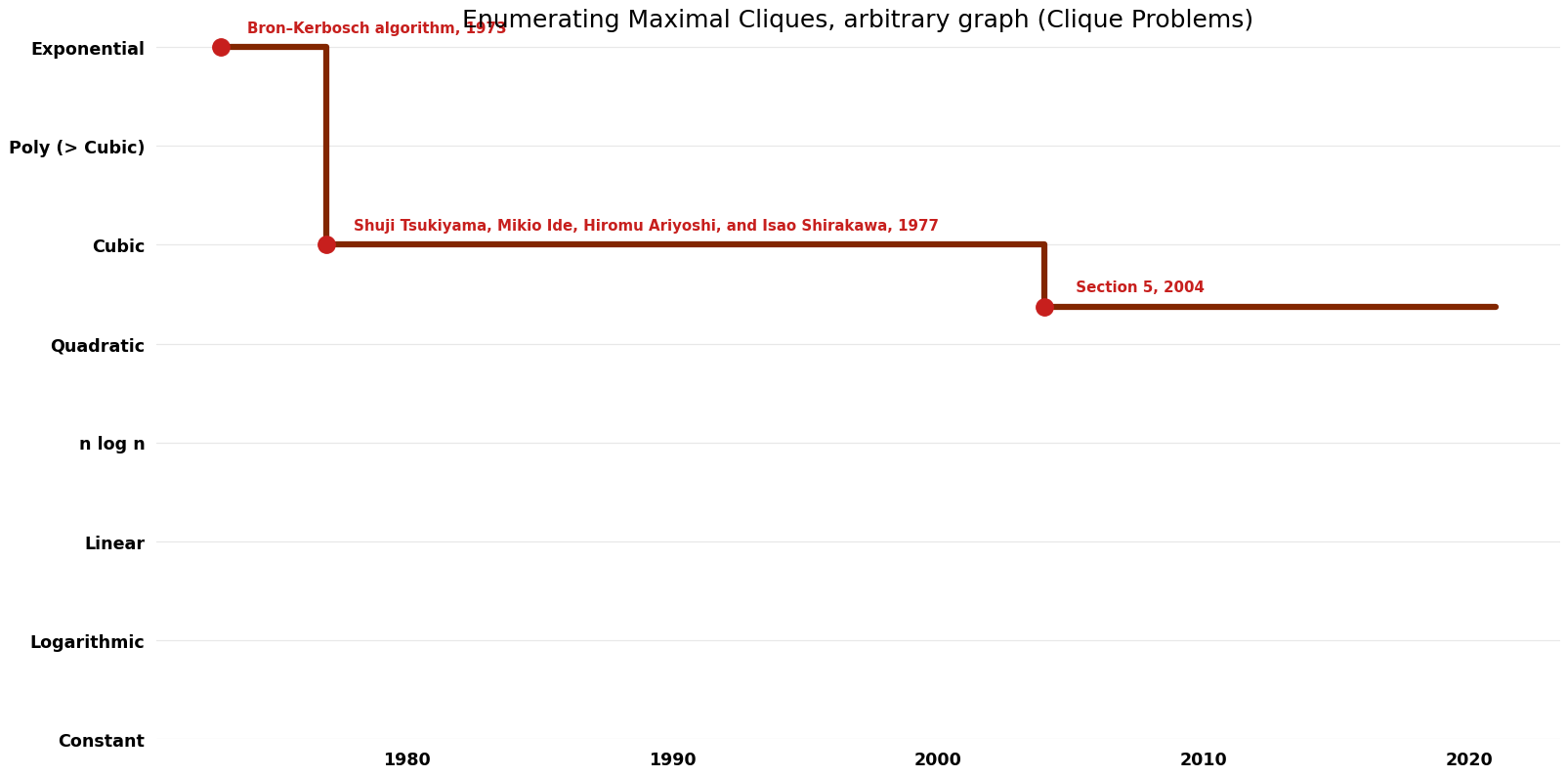
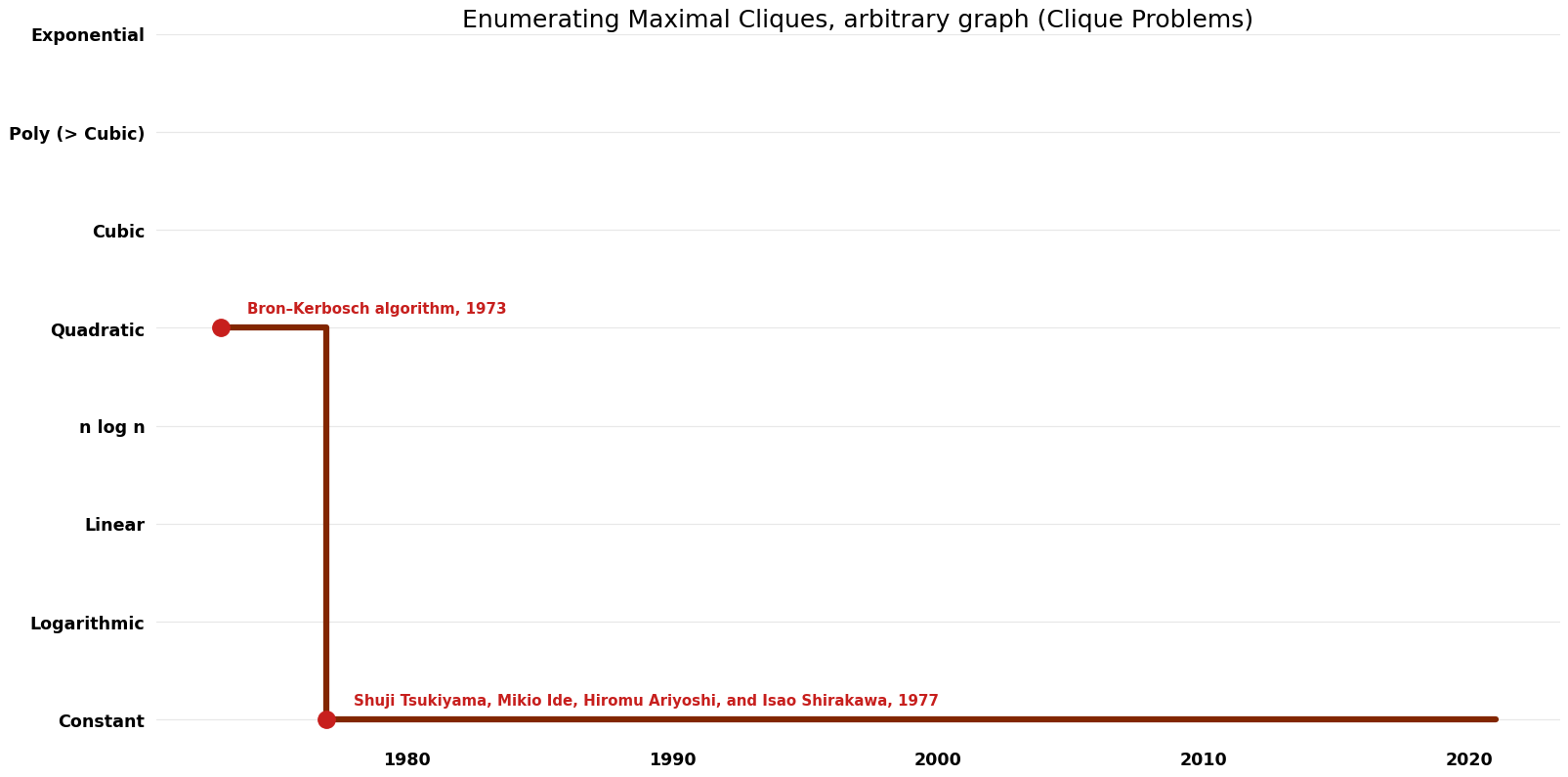
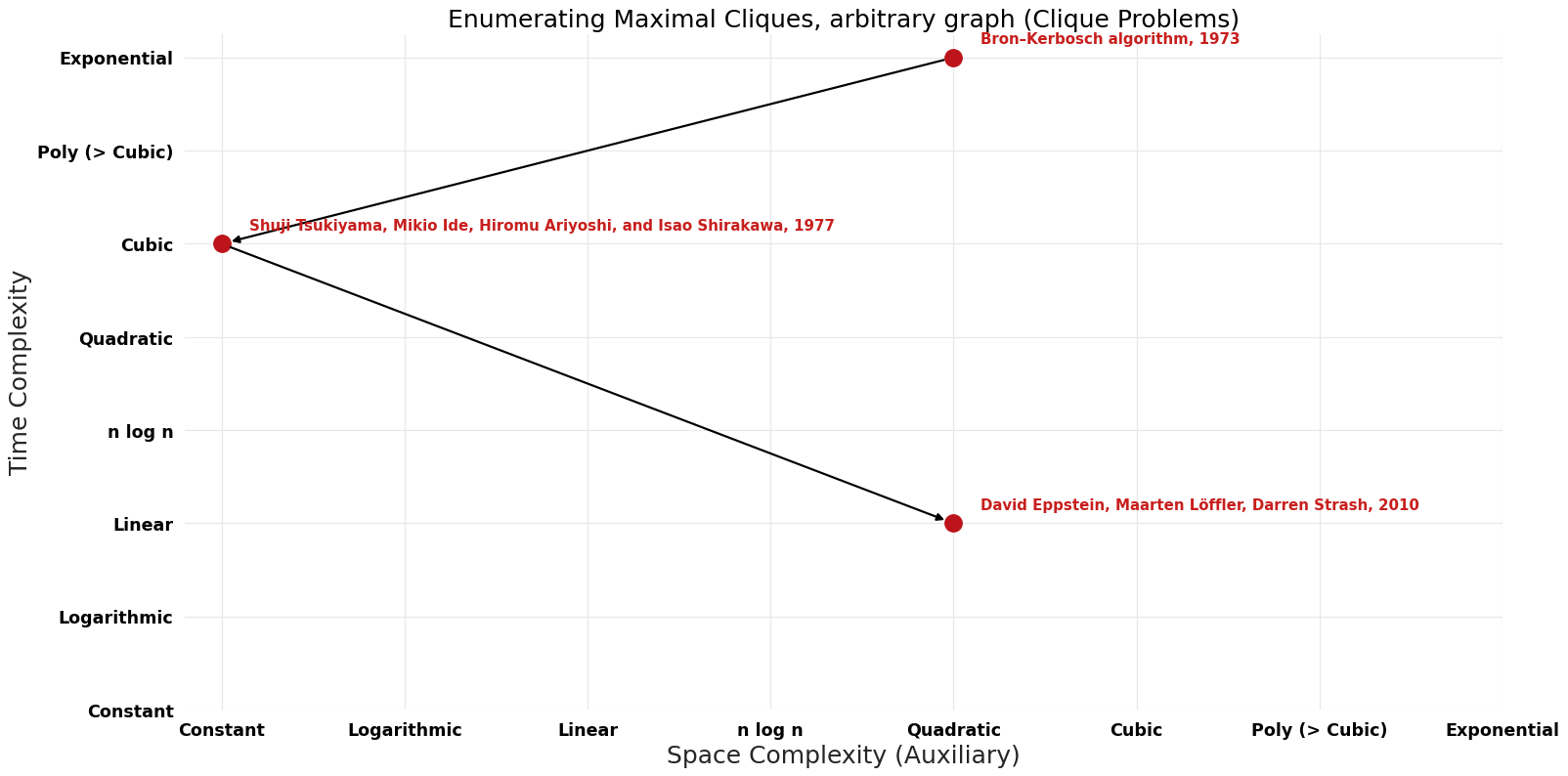
Table of Algorithms

Name	Year	Time	Space	Approximation Factor	Model	Reference
Bron–Kerbosch algorithm	1973	$O({3}^{(n/{3})})$	$O(n^{2})$ auxiliary?	Exact	Deterministic	Time
Akkoyunlu; E. A.	1973	$O({3}^{(n/{3})$})	$O(n^{2})$ auxiliary??	Exact	Deterministic	Time
Tomita; Tanaka & Takahashi	2006	$O({3}^{(n/{3})$})	$O(n^{2})$ auxiliary?	Exact	Deterministic	Time
Segundo; Artieda; Strash Parallel	2011	$O({3}^{(n/{3})})$ total work? (previously this cell said $O(n^{4})$)	$O(n^{2})$ auxiliary??	Exact	Parallel	Time
David Eppstein, Maarten Löffler, Darren Strash	2010	$O(dn {3}^{(d/{3})})$	$O(n^{2})$ auxiliary?	Exact	Deterministic	Time
Chiba and Nishizeki	1985	$O(a(G)*m)$ per clique	$O(m)$ auxiliary	Exact	Deterministic	Time & Space
M. Chrobak and D. Eppstein	1989	$O(n d^{2} {2}^d)$	$O(n)$ auxiliary?	Exact	Deterministic	Time
Shuji Tsukiyama, Mikio Ide, Hiromu Ariyoshi, and Isao Shirakawa	1977	$O(nm)$ per clique	$O(m)$ auxiliary	Exact	Deterministic	Time
Kazuhisa Makino, Takeaki Uno; Section 5	2004	$O(n^{\omega})$ per clique where omega is the exponent on matrix multiplication	$O(n^{2})$ auxiliary	Exact	Deterministic	Time & Space
Kazuhisa Makino, Takeaki Uno; Section 6	2004	$O(delta^{4})$	$O(n+m)$ auxiliary(?)	Exact	Deterministic	Time & Space

Time Complexity graph

Space Complexity graph

Pareto Decades graph