Cyclic Nontrivial SCCs DFA Minimization: Difference between revisions
Jump to navigation
Jump to search
(Created page with "{{DISPLAYTITLE:Cyclic Nontrivial SCCs DFA Minimization (DFA Minimization)}} == Description == Given an finite deterministic automaton (DFA) from a class $C$ of DFAs, whose nontrivial SCCs are cyclic, determine its minimal automaton given by the equivalence relation on states. == Related Problems == Generalizations: DFA Minimization Related: Acyclic DFA Minimization == Parameters == <pre>$n$: number of states $d$: number of transitions $k$: size of alphab...") |
No edit summary |
||
| Line 12: | Line 12: | ||
== Parameters == | == Parameters == | ||
$n$: number of states | |||
$d$: number of transitions | $d$: number of transitions | ||
$k$: size of alphabet | |||
$k$: size of alphabet | |||
== Table of Algorithms == | == Table of Algorithms == | ||
Revision as of 12:02, 15 February 2023
Description
Given an finite deterministic automaton (DFA) from a class $C$ of DFAs, whose nontrivial SCCs are cyclic, determine its minimal automaton given by the equivalence relation on states.
Related Problems
Generalizations: DFA Minimization
Related: Acyclic DFA Minimization
Parameters
$n$: number of states
$d$: number of transitions
$k$: size of alphabet
Table of Algorithms
| Name | Year | Time | Space | Approximation Factor | Model | Reference |
|---|---|---|---|---|---|---|
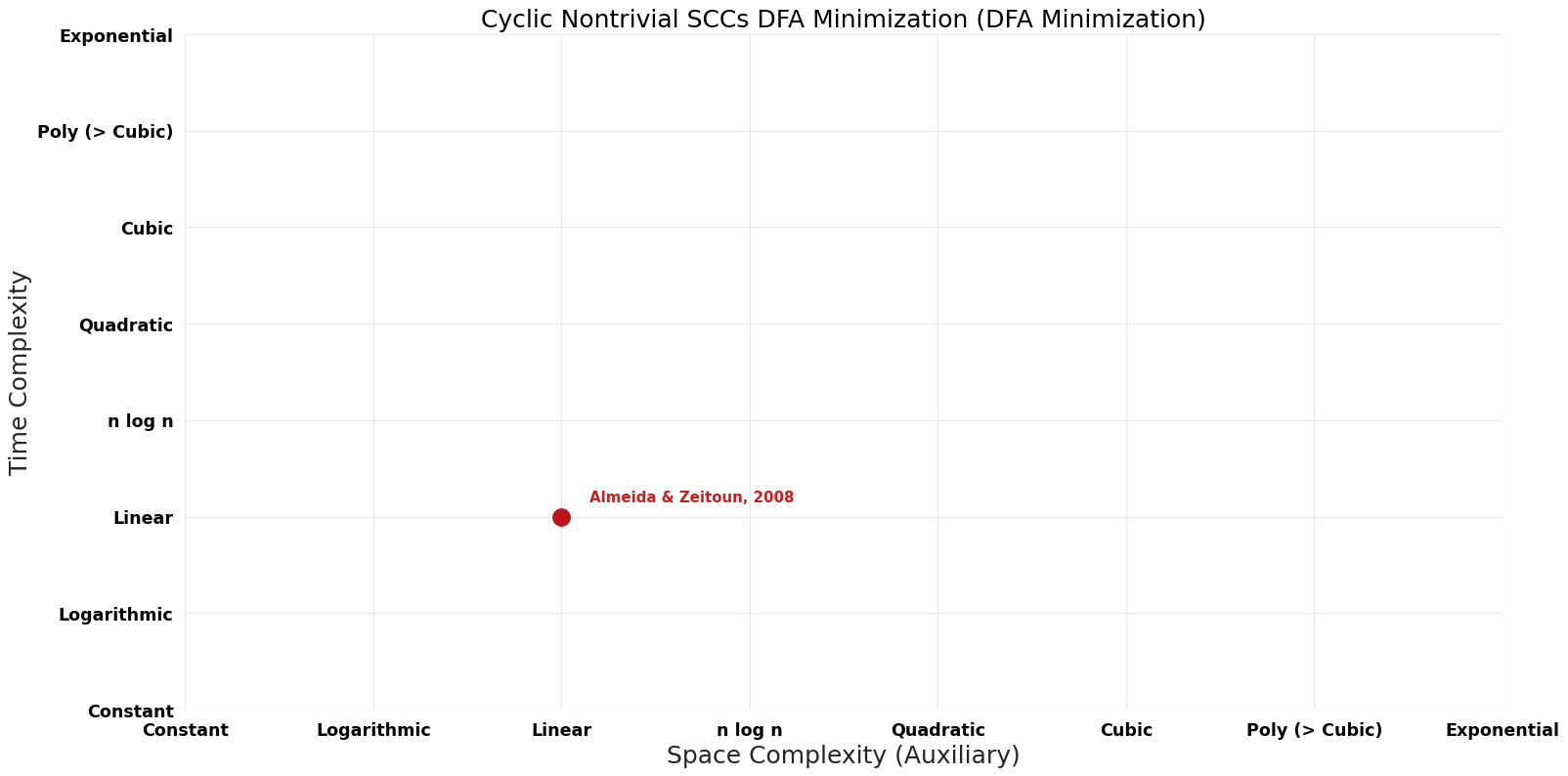
| Almeida & Zeitoun | 2008 | $O(n)$ | $O(n)$ | Exact | Deterministic | Time & Space |
Time Complexity graph
Space Complexity graph
Pareto Decades graph
