DFA Minimization: Difference between revisions
Jump to navigation
Jump to search
No edit summary |
No edit summary |
||
| Line 12: | Line 12: | ||
== Parameters == | == Parameters == | ||
$n$: number of states | |||
$d$: number of transitions | $d$: number of transitions | ||
$k$: size of alphabet | |||
$k$: size of alphabet | |||
== Table of Algorithms == | == Table of Algorithms == | ||
Revision as of 12:02, 15 February 2023
Description
Given a finite deterministic automaton (DFA) from a class $C$ of DFAs, determine its minimal automaton given by the equivalence relation on states.
Related Problems
Subproblem: Acyclic DFA Minimization, Cyclic Nontrivial SCCs DFA Minimization
Related: Cyclic Nontrivial SCCs DFA Minimization
Parameters
$n$: number of states
$d$: number of transitions
$k$: size of alphabet
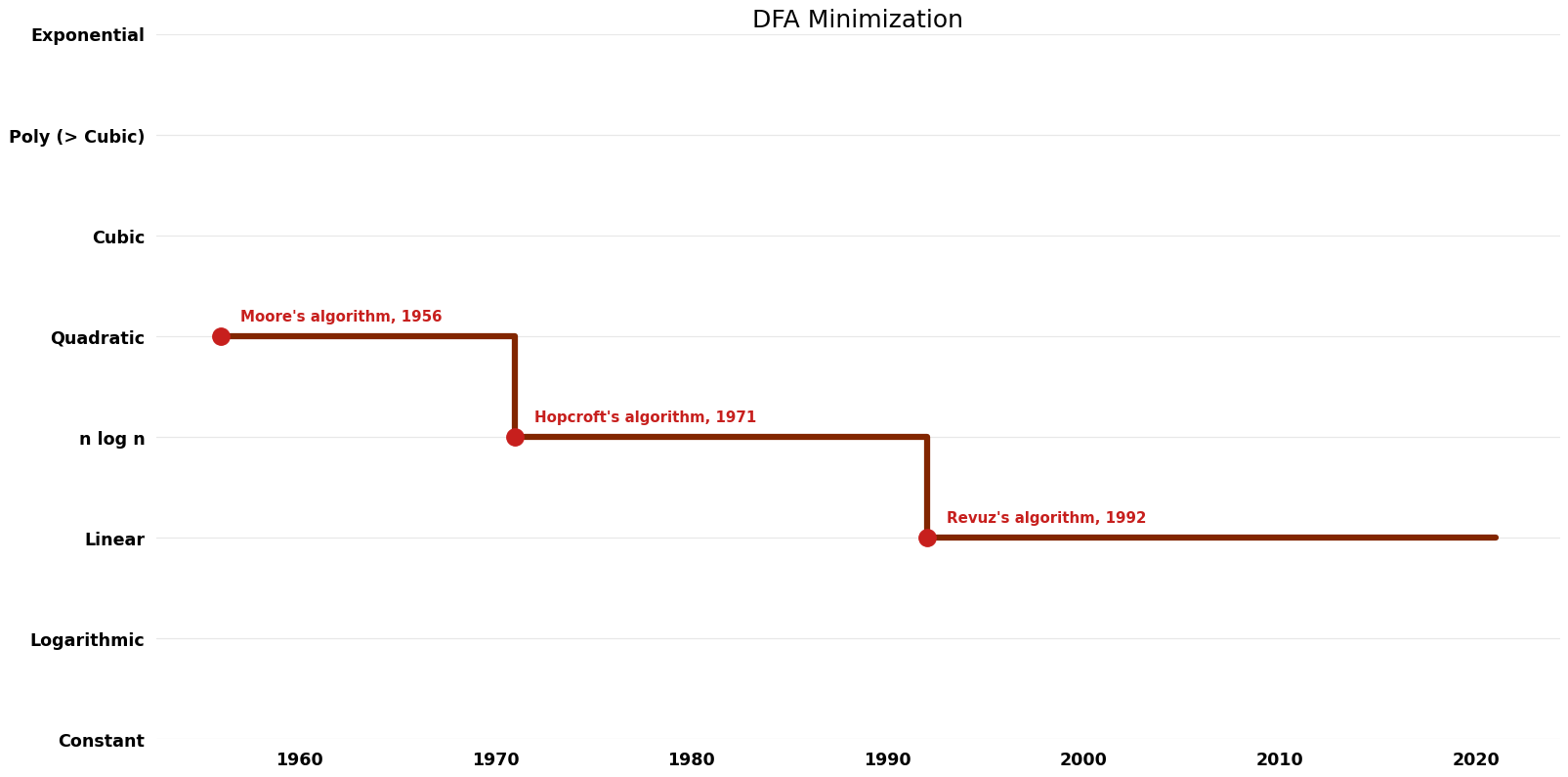
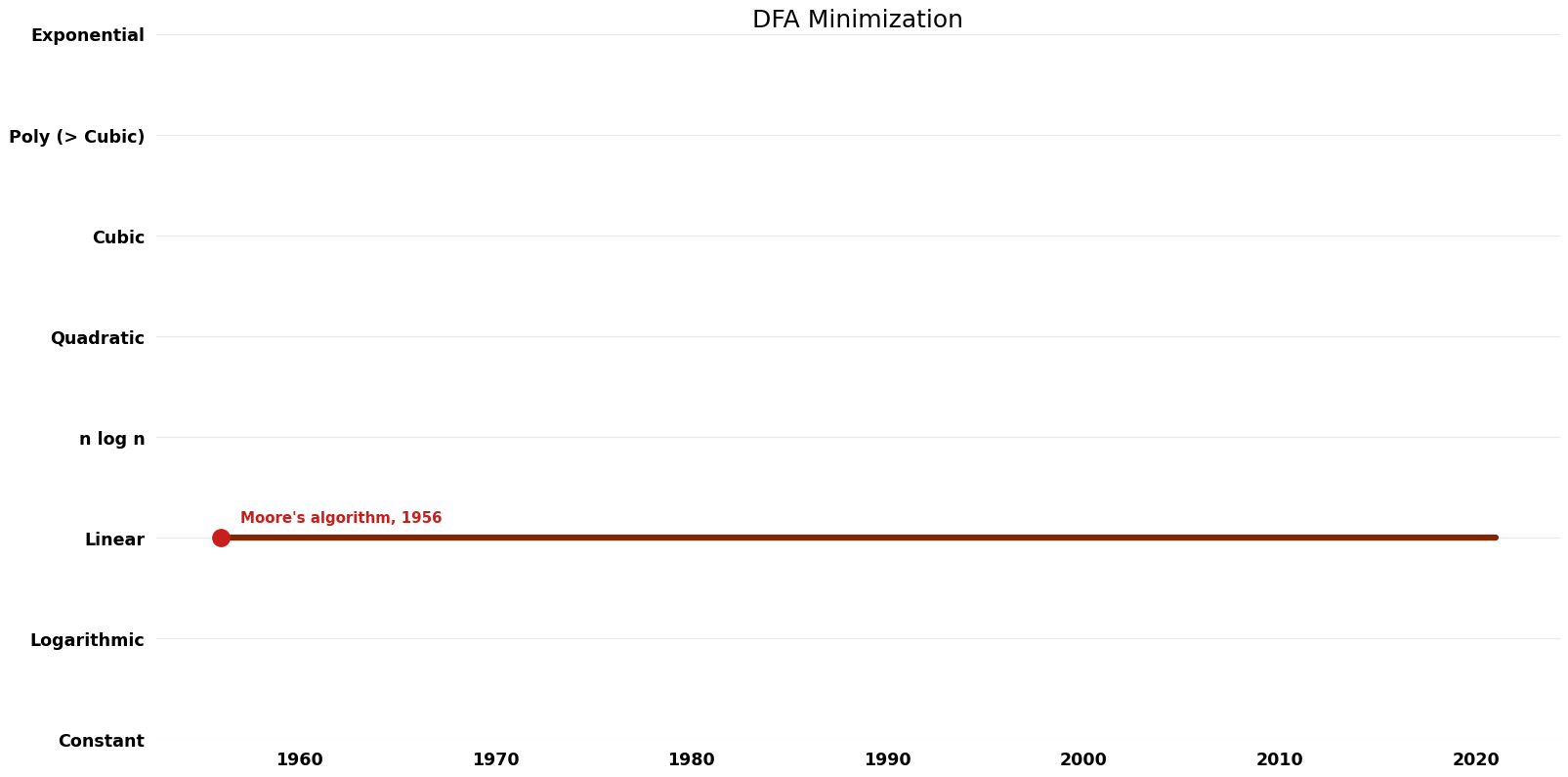
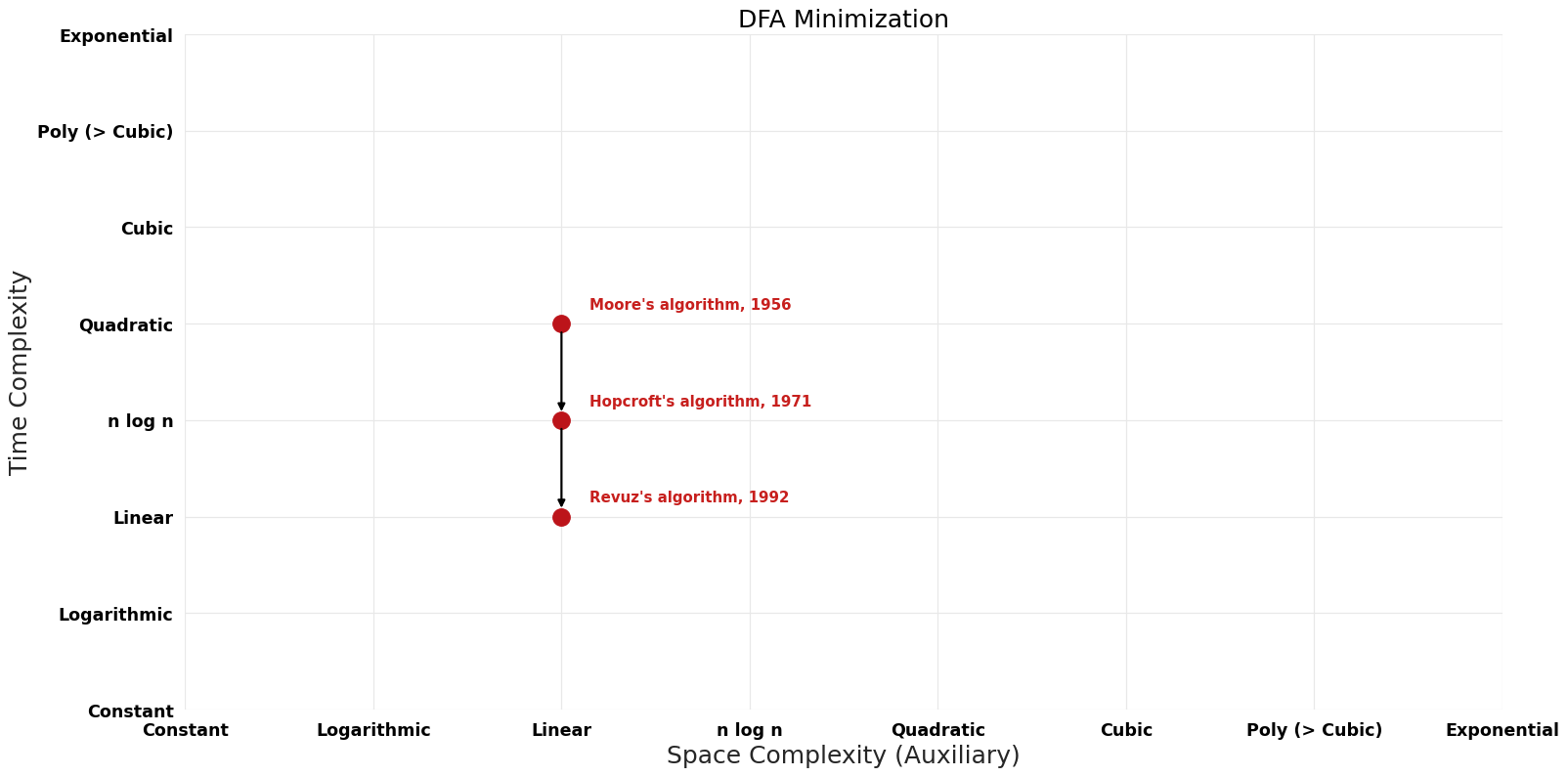
Table of Algorithms
| Name | Year | Time | Space | Approximation Factor | Model | Reference |
|---|---|---|---|---|---|---|
| Hopcroft's algorithm | 1971 | $O(kn \log n)$ | $O(kn)$ | Exact | Deterministic | Time & Space |
| Moore's algorithm | 1956 | $O(n^{2} k)$ | $O(n)$ | Exact | Deterministic | Time |
| Brzozowski's algorithm | 1963 | $O({2}^n)$ | $O({2}^n)$ | Exact | Deterministic | Time & Space |
Time Complexity graph
Space Complexity graph
Pareto Decades graph
