Reporting all intersection points, line segments

Description

The line segment intersection problem supplies a list of line segments in the Euclidean plane and asks about the points where they intersect (cross), if any. In this case, we wish to report all points of intersection.

Related Problems

Generalizations: Reporting all intersection points, generalized segments

Subproblem: Counting number of intersection points, line segments

Related: Reporting all intersection points, convex polygons, Reporting all intersection points, general polygons

Parameters

n: number of line segments

k: number of points of intersection

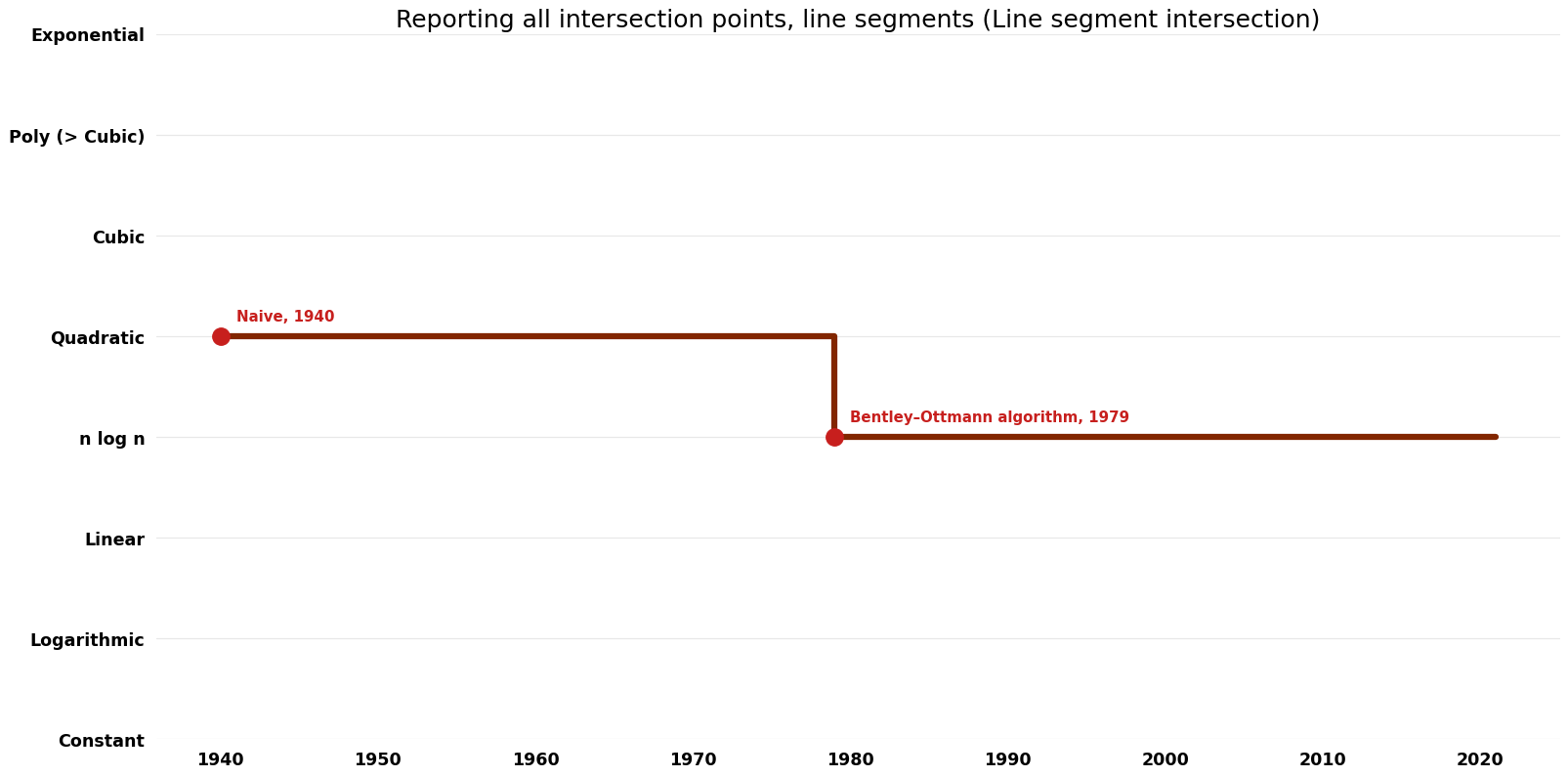
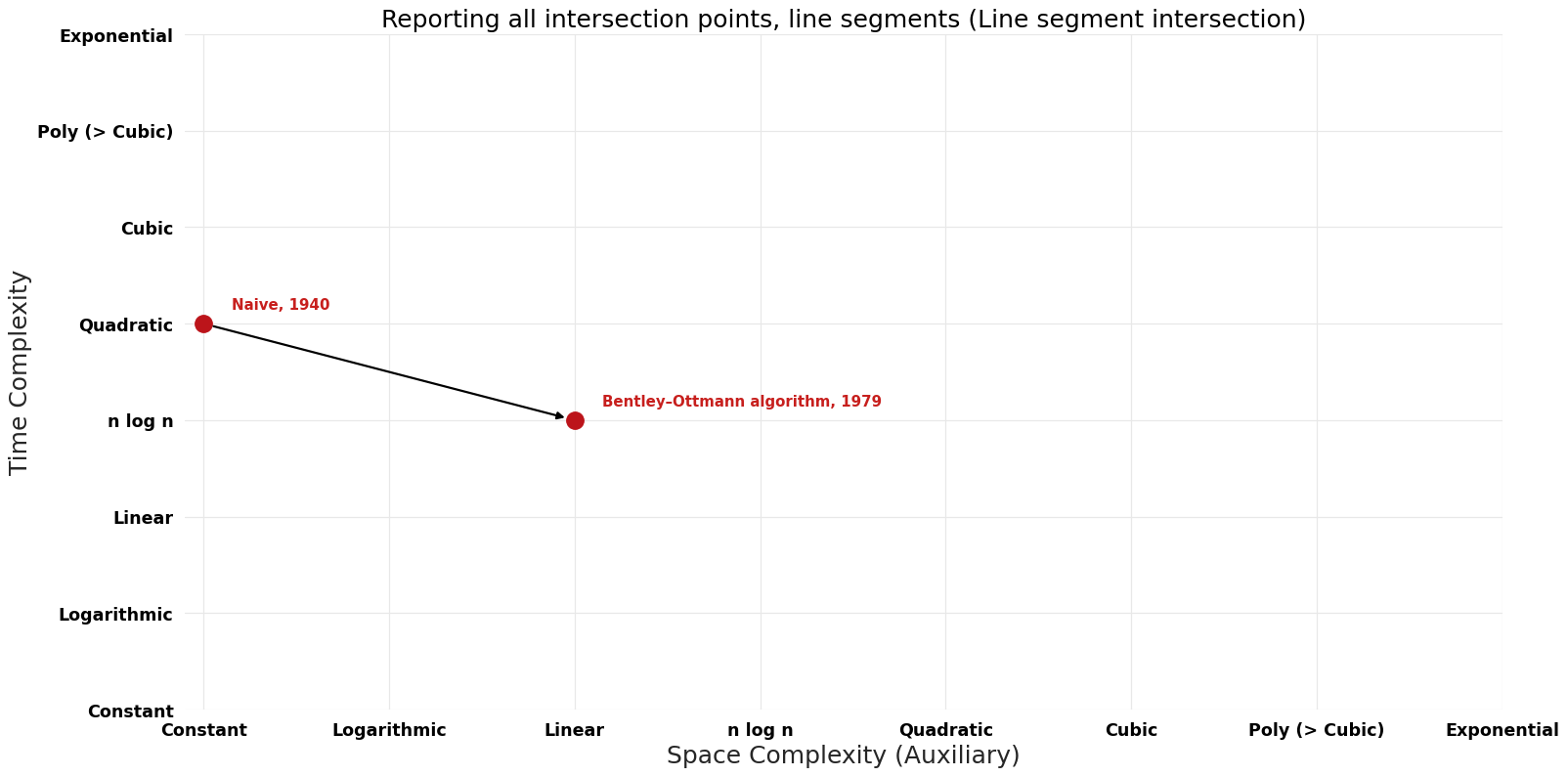
Table of Algorithms

Name	Year	Time	Space	Approximation Factor	Model	Reference
Naive	1940	$O(n^{2})$	$O(n+k)$ total ($O({1})$ auxiliary if excluding input and output)	Exact	Deterministic
Bentley–Ottmann algorithm	1979	$O( n log n + k log n)$	$O(n)$ auxiliary	Exact	Deterministic	Time & Space
Chazelle & Edelsbrunner	1992	$O( nlog n + k )$	$O(n+k)$ total?	Exact	Deterministic	Time & Space
CHAZELLE	1986	$O( n*log^{2}(n)/(log log n) + k)$	$O(n+k)$ total (and possibly auxiliary as well?)	Exact	Deterministic	Time & Space
Goodrich	1989	$O(log^{2}(n))$	$O(n+k)$ total?	Exact	Parallel	Time

Time Complexity graph

Space Complexity graph

Pareto Decades graph

References/Citation

https://dl.acm.org/doi/10.1145/147508.147511

https://dl.acm.org/doi/10.1145/304893.304991)