Longest Common Subsequence: Difference between revisions
Jump to navigation
Jump to search
(Created page with "{{DISPLAYTITLE:Longest Common Subsequence (Longest Common Subsequence)}} == Description == The longest common subsequence (LCS) problem is the problem of finding the longest subsequence common to all sequences in a set of sequences (often just two sequences). == Related Problems == Subproblem: Longest Common Substring with don't cares == Parameters == <pre>$n$: length of the longer input string $m$: length of the shorter input string $r$: length of the LCS $s...") |
No edit summary |
||
| Line 10: | Line 10: | ||
== Parameters == | == Parameters == | ||
$n$: length of the longer input string | |||
$m$: length of the shorter input string | $m$: length of the shorter input string | ||
$r$: length of the LCS | $r$: length of the LCS | ||
$s$: size of the alphabet | $s$: size of the alphabet | ||
$p$: the number of dominant matches (AKA number of minimal candidates), i.e. the total number of ordered pairs of positions at which the two sequences match | |||
$p$: the number of dominant matches (AKA number of minimal candidates), i.e. the total number of ordered pairs of positions at which the two sequences match | |||
== Table of Algorithms == | == Table of Algorithms == | ||
Revision as of 13:02, 15 February 2023
Description
The longest common subsequence (LCS) problem is the problem of finding the longest subsequence common to all sequences in a set of sequences (often just two sequences).
Related Problems
Subproblem: Longest Common Substring with don't cares
Parameters
$n$: length of the longer input string
$m$: length of the shorter input string
$r$: length of the LCS
$s$: size of the alphabet
$p$: the number of dominant matches (AKA number of minimal candidates), i.e. the total number of ordered pairs of positions at which the two sequences match
Table of Algorithms
Currently no algorithms in our database for the given problem.
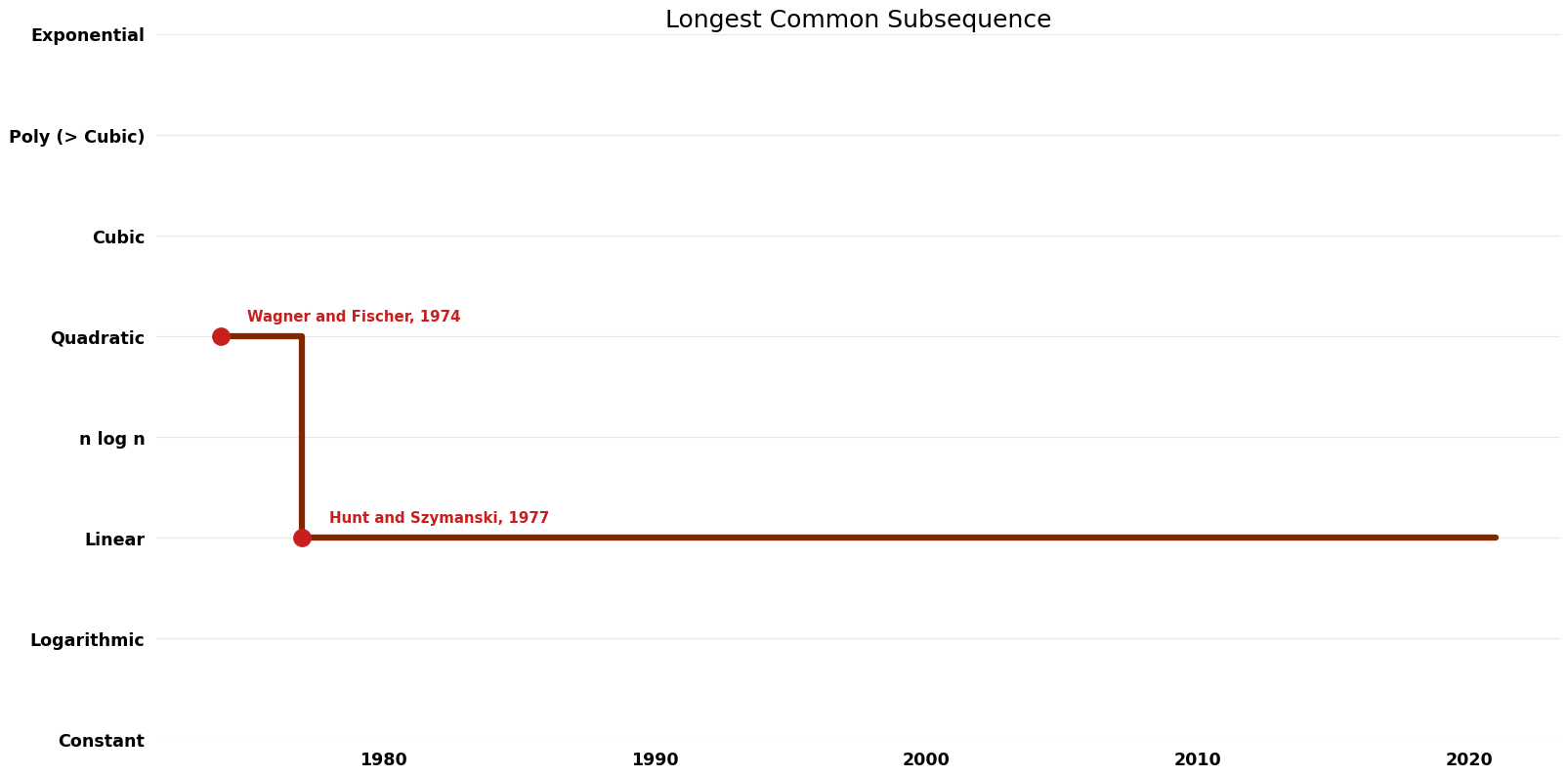
Time Complexity graph
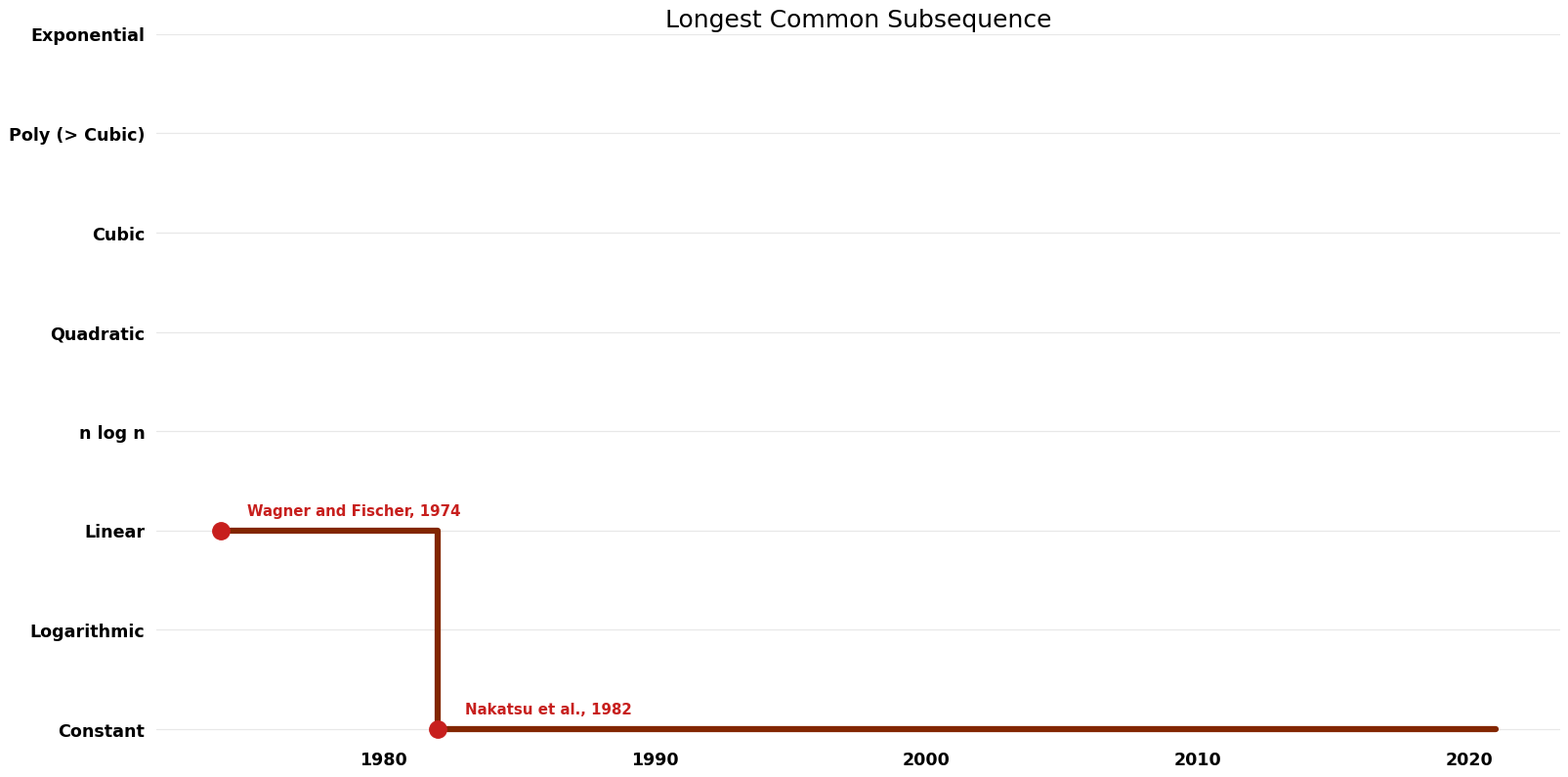
Space Complexity graph
Pareto Decades graph
Reductions FROM Problem
| Problem | Implication | Year | Citation | Reduction |
|---|---|---|---|---|
| UOV | If: to-time: $O((nm)^{({1}-\epsilon)})$, where $|x| = O(nd)$ and $|y| = O(md)$ Then: from-time: $O((nm)^{({1}-\epsilon/{2})})$ |
2015 | https://arxiv.org/pdf/1502.01063.pdf | link |
References/Citation
https://link.springer.com/chapter/10.1007/978-3-662-43948-7_4