Matrix Chain Ordering Problem: Difference between revisions
Jump to navigation
Jump to search
(Created page with "{{DISPLAYTITLE:Matrix Chain Ordering Problem (Matrix Chain Multiplication)}} == Description == Matrix chain multiplication (or Matrix Chain Ordering Problem; MCOP) is an optimization problem. Given a sequence of matrices, the goal is to find the most efficient way to multiply these matrices. == Related Problems == Subproblem: Approximate MCOP, Matrix Chain Scheduling Problem Related: Matrix Chain Scheduling Problem, Approximate MCSP == Parameters...") |
No edit summary |
||
| Line 12: | Line 12: | ||
== Parameters == | == Parameters == | ||
$n$: number of matrices | |||
== Table of Algorithms == | == Table of Algorithms == | ||
Revision as of 13:02, 15 February 2023
Description
Matrix chain multiplication (or Matrix Chain Ordering Problem; MCOP) is an optimization problem. Given a sequence of matrices, the goal is to find the most efficient way to multiply these matrices.
Related Problems
Subproblem: Approximate MCOP, Matrix Chain Scheduling Problem
Related: Matrix Chain Scheduling Problem, Approximate MCSP
Parameters
$n$: number of matrices
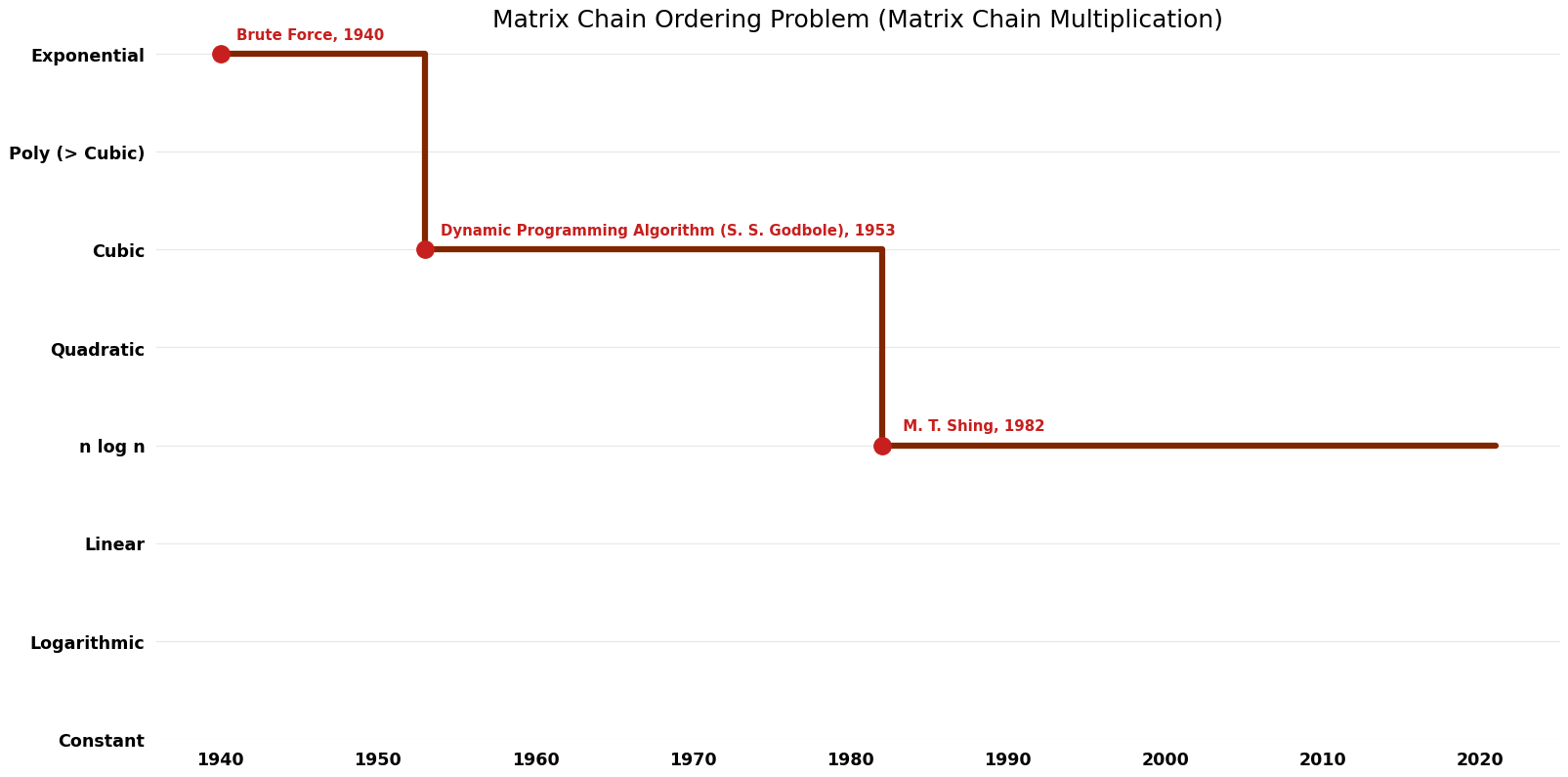
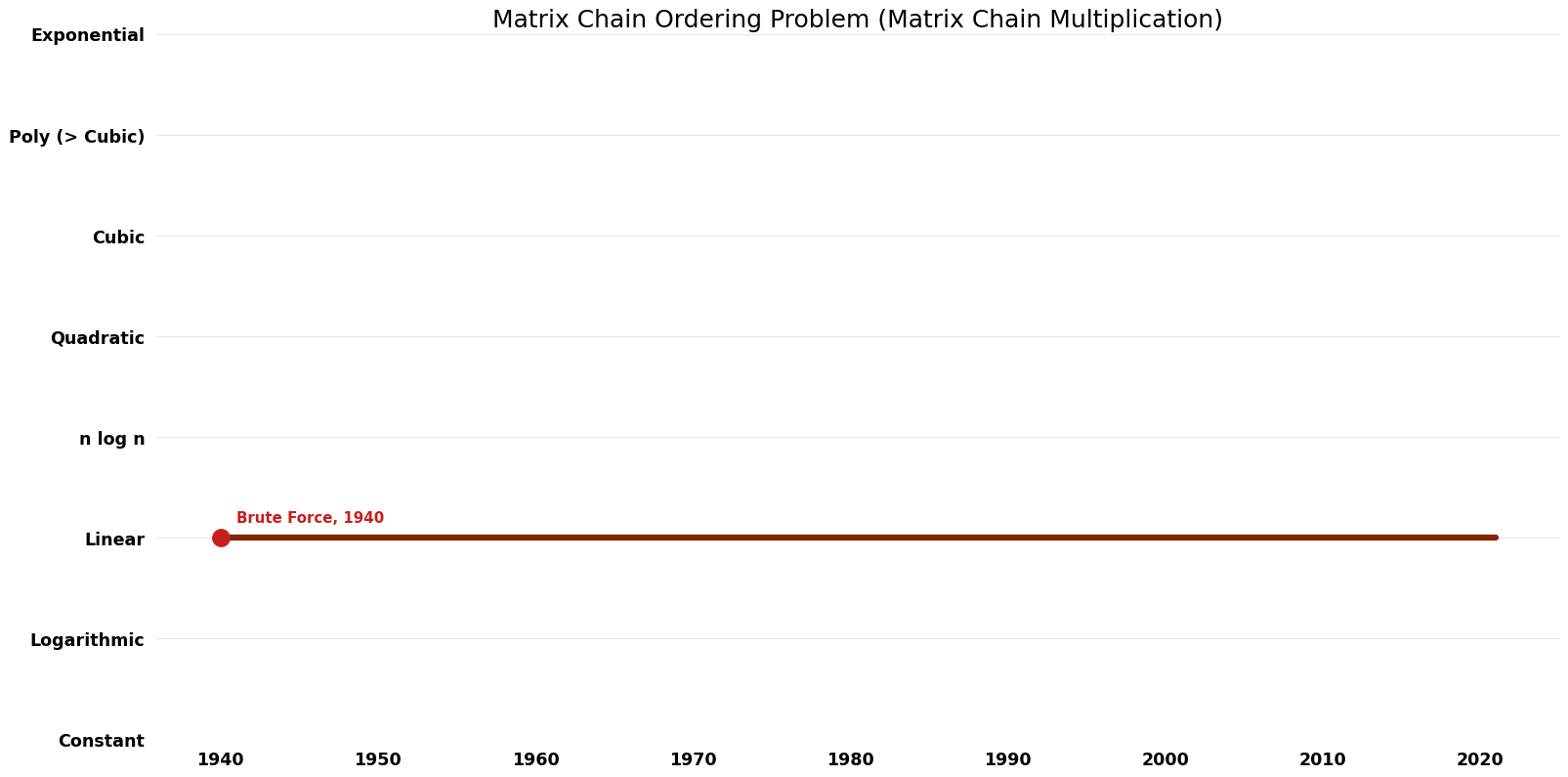
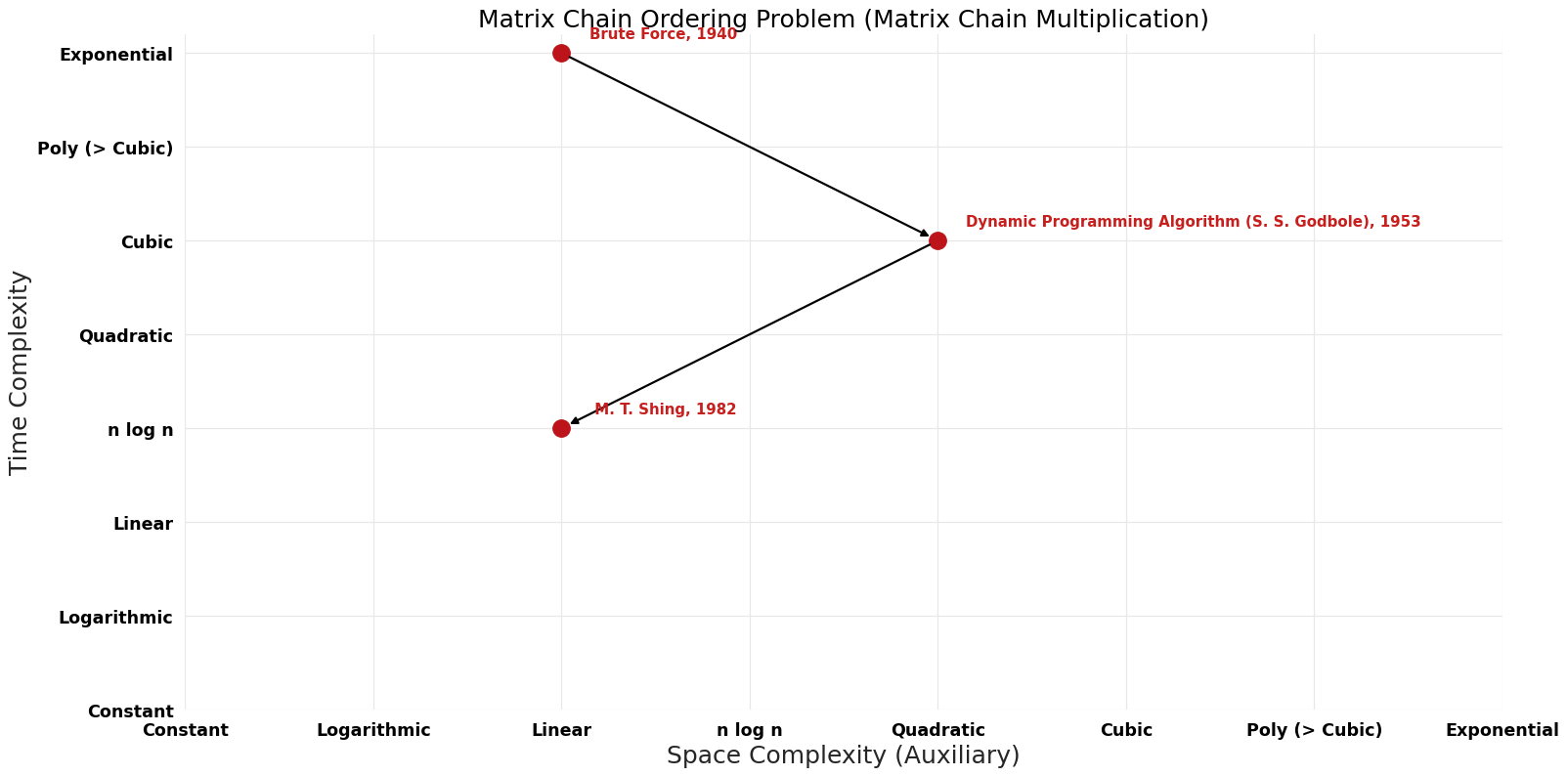
Table of Algorithms
| Name | Year | Time | Space | Approximation Factor | Model | Reference |
|---|---|---|---|---|---|---|
| Brute Force | 1940 | O ({4}^n) | $O(n)$ | Exact | Deterministic | |
| Dynamic Programming Algorithm (S. S. Godbole) | 1953 | $O(n^{3})$ | $O(n^{2})$ | Exact | Deterministic | |
| T. C. Hu ; M. T. Shing | 1982 | $O(nlogn)$ | $O(n)$ | Exact | Deterministic | Time |
Time Complexity graph
Space Complexity graph
Pareto Decades graph
References/Citation
https://citeseerx.ist.psu.edu/viewdoc/citations?doi=10.1.1.695.2923