BCNF Decomposition: Difference between revisions
Jump to navigation
Jump to search
(Created page with "== Problem Description== == Bounds Chart == 350px == Step Chart == 350px == Improvement Table == {| class="wikitable" style="text-align:center;" width="100%" !width="20%" | Complexity Classes !! width="40%" | Algorithm Paper Links !! width="40%" | Lower Bounds Paper Links |- | rowspan="1" | Exp/Factorial | | |- | rowspan="1" | Polynomial > 3 | | |- | rowspan="1" | Cubic | | |- | ro...") |
No edit summary |
||
| Line 1: | Line 1: | ||
== | {{DISPLAYTITLE:BCNF Decomposition (BCNF Decomposition)}} | ||
== Description == | |||
BCNF Decomposition is the problem of decomposing a relation schema into Boyce-Codd normal form (BCNF). | |||
= | A relation schema $R$ is in Boyce Codd Normal Form (abbr. BCNF) if for all non-trivial FDs $X \rightarrow Y$ in $F^+$, $X$ is a superkey. In extending this notion to database schemas, we must be conscious of the UR-assumption. We say that $R_i = <ATTR_i,F_i>$ is in BCNF if the schema $<ATTR_i, F^+(ATTR_i)>$ is in BCNF, and $D$ is in BCNF if each $R_i$ is. | ||
== | == Related Problems == | ||
== | Related: [[Decisional BCNF]] | ||
== Parameters == | |||
No parameters found. | |||
== Table of Algorithms == | |||
Currently no algorithms in our database for the given problem. | |||
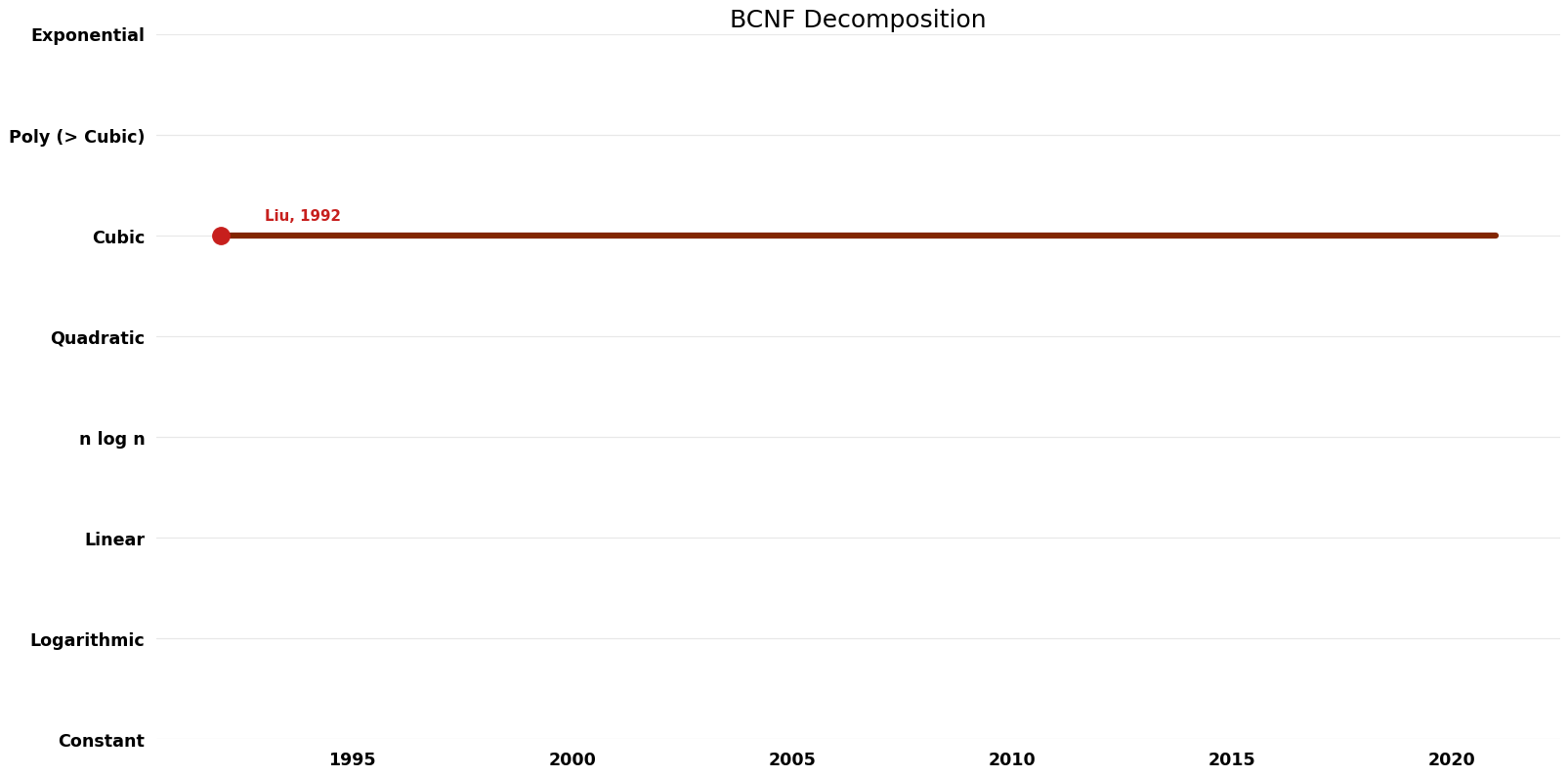
| | == Time Complexity graph == | ||
[[File:BCNF Decomposition - Time.png|1000px]] | |||
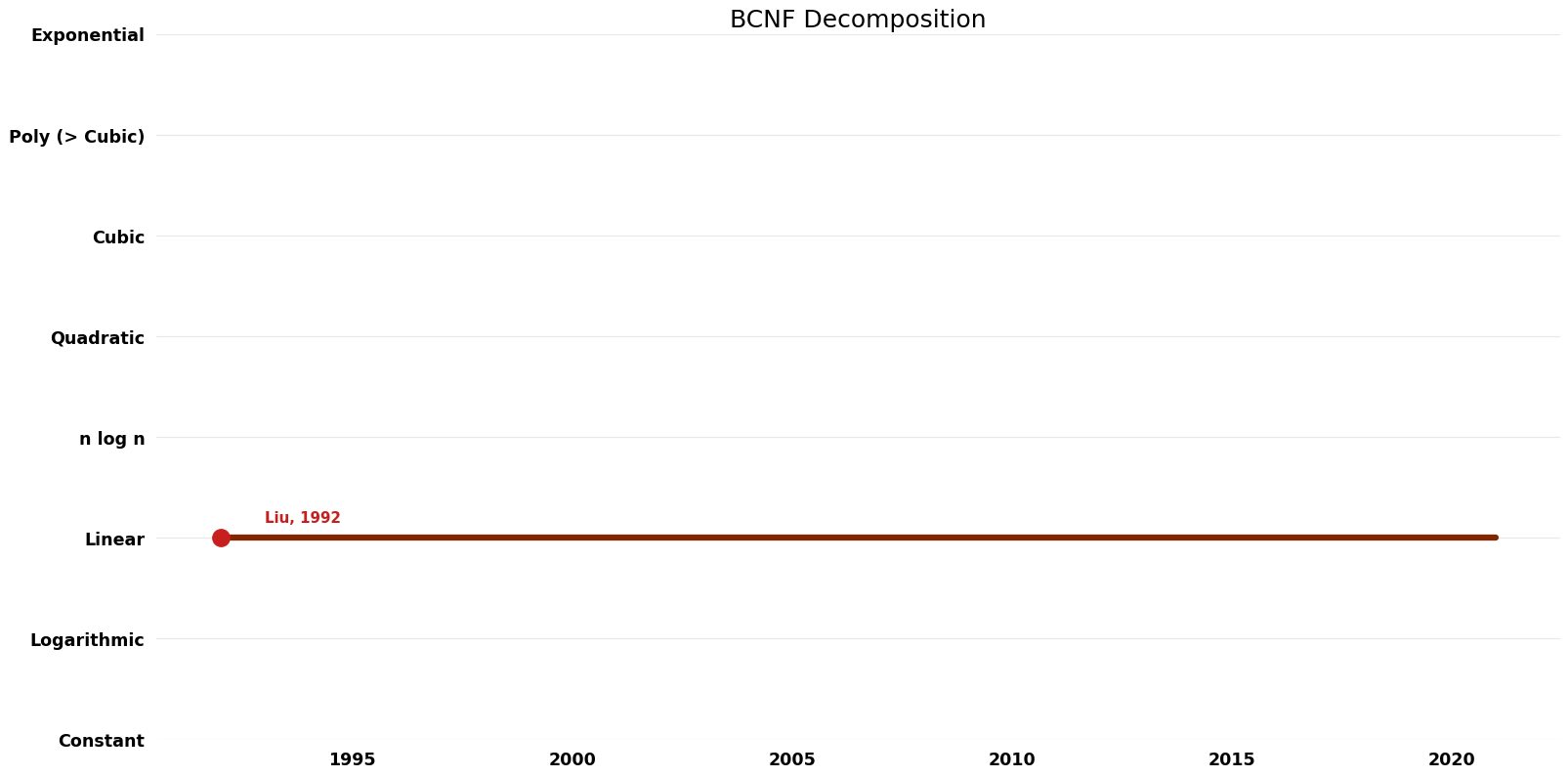
| | == Space Complexity graph == | ||
[[File:BCNF Decomposition - Space.png|1000px]] | |||
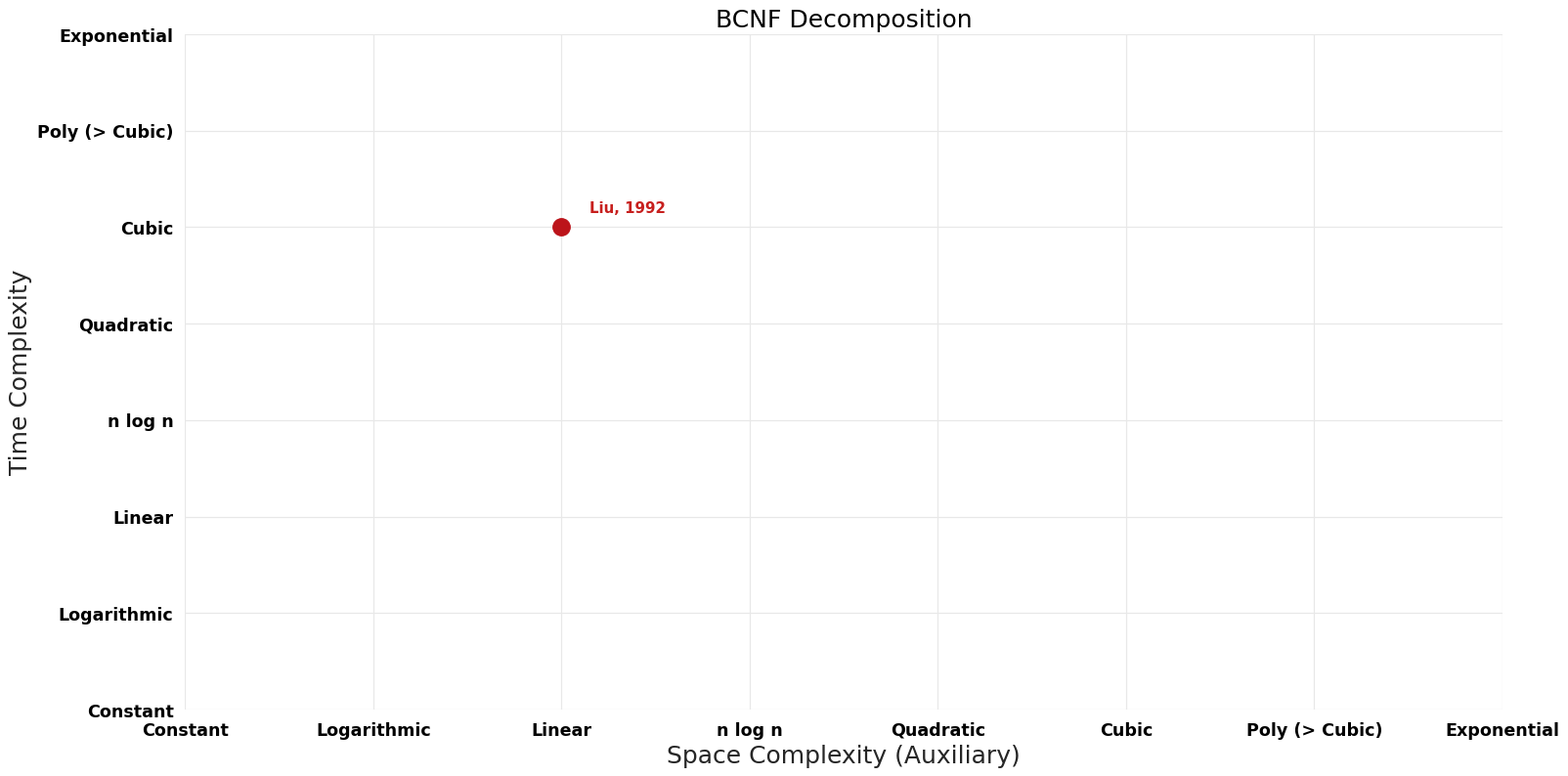
== Pareto Decades graph == | |||
[[File:BCNF Decomposition - Pareto Frontier.png|1000px]] | |||
Revision as of 11:22, 15 February 2023
Description
BCNF Decomposition is the problem of decomposing a relation schema into Boyce-Codd normal form (BCNF).
A relation schema $R$ is in Boyce Codd Normal Form (abbr. BCNF) if for all non-trivial FDs $X \rightarrow Y$ in $F^+$, $X$ is a superkey. In extending this notion to database schemas, we must be conscious of the UR-assumption. We say that $R_i = <ATTR_i,F_i>$ is in BCNF if the schema $<ATTR_i, F^+(ATTR_i)>$ is in BCNF, and $D$ is in BCNF if each $R_i$ is.
Related Problems
Related: Decisional BCNF
Parameters
No parameters found.
Table of Algorithms
Currently no algorithms in our database for the given problem.