Topological Sorting: Difference between revisions
Jump to navigation
Jump to search
(Created page with "== Problem Description== Topological sorting for Directed Acyclic Graph (DAG) is a linear ordering of vertices such that for every directed edge u v, vertex u comes before v in the ordering. Topological Sorting for a graph is not possible if the graph is not a DAG. Topological Sorting is mainly used for scheduling jobs from the given dependencies among jobs. In computer science, applications of this type arise in instruction scheduling, ordering of formula cell evaluati...") |
No edit summary |
||
| Line 1: | Line 1: | ||
== | {{DISPLAYTITLE:Topological Sorting (Topological Sorting)}} | ||
== Description == | |||
Given a graph or network, find a topological sorting of the graph. A list in topological order has a special property. Simply expressed: proceeding from element to element along any path in the network, one passes through the list in one direction only. Stated another way, a list in topological order is such that no element appears in it until after all elements appearing on all paths leading to the particular element have been listed. | |||
== | == Parameters == | ||
== | <pre>V: number of vertices | ||
E: number of edges</pre> | |||
== Table of Algorithms == | |||
{| class="wikitable sortable" style="text-align:center;" width="100%" | |||
! Name !! Year !! Time !! Space !! Approximation Factor !! Model !! Reference | |||
|- | |- | ||
| | |||
| | | [[Kahn's algorithm (Topological Sorting Topological Sorting)|Kahn's algorithm]] || 1962 || $O(V+E)$ || $O(V)$ auxiliary || Exact || Deterministic || [https://dl.acm.org/doi/10.1145/368996.369025 Time] | ||
| | |||
|- | |- | ||
| | | [[Tarjan's DFS based algorithm (Topological Sorting Topological Sorting)|Tarjan's DFS based algorithm]] || 1976 || $O(V+E)$ || $O(V)$ auxiliary? || Exact || Deterministic || [https://link.springer.com/article/10.1007/BF00268499 Time] | ||
| | |||
| | |||
|- | |- | ||
| | | [[Dekel; Nassimi & Sahni Parallel Implementation (Topological Sorting Topological Sorting)|Dekel; Nassimi & Sahni Parallel Implementation ]] || 1981 || $O( log² V)$ || $O(V^{2})$?? || Exact || Parallel || [https://www.proquest.com/docview/920003939?pq-origsite=gscholar&fromopenview=true Time] | ||
| | |||
| | |||
|- | |- | ||
| | |} | ||
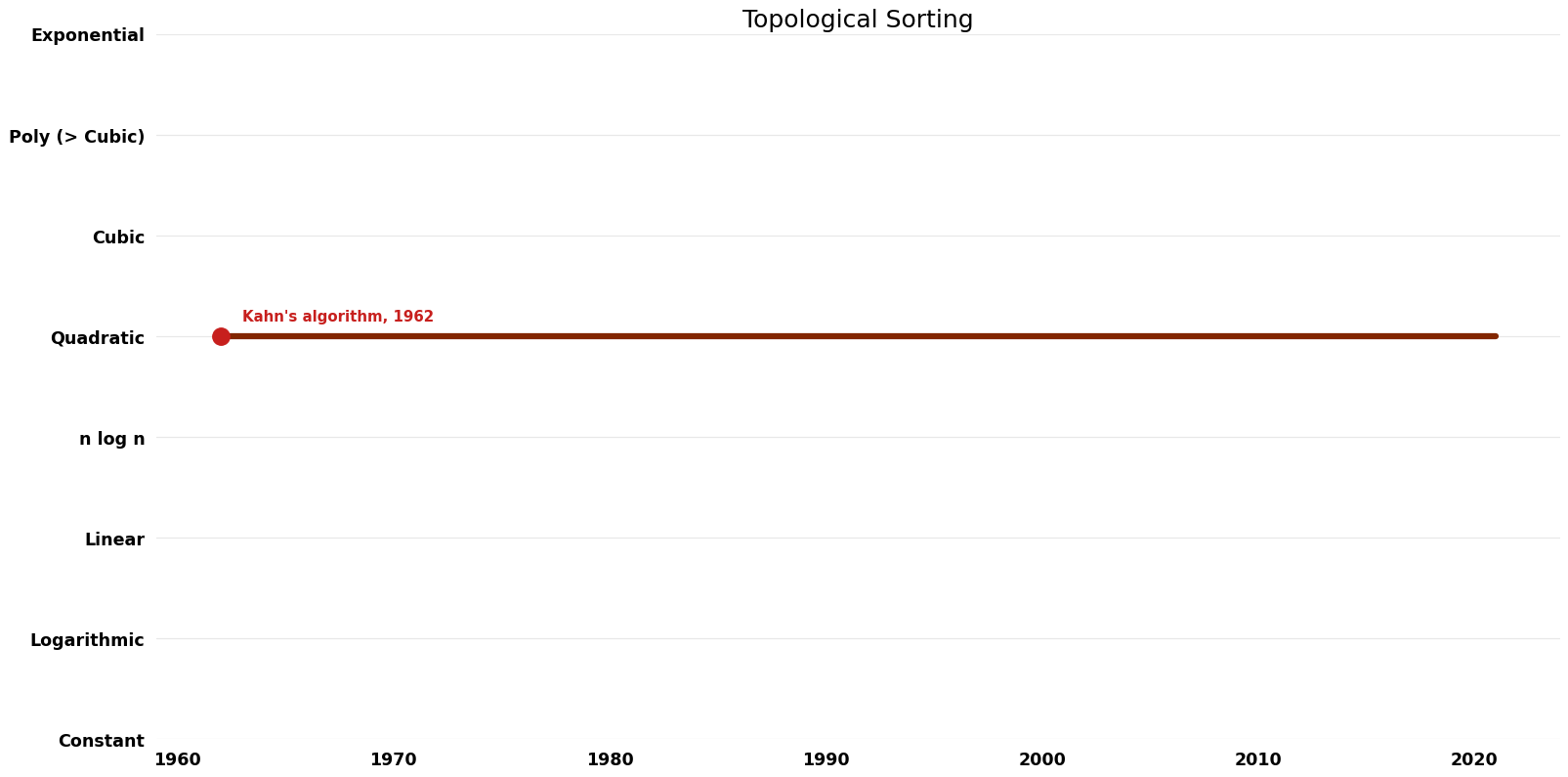
| | == Time Complexity graph == | ||
[[File:Topological Sorting - Time.png|1000px]] | |||
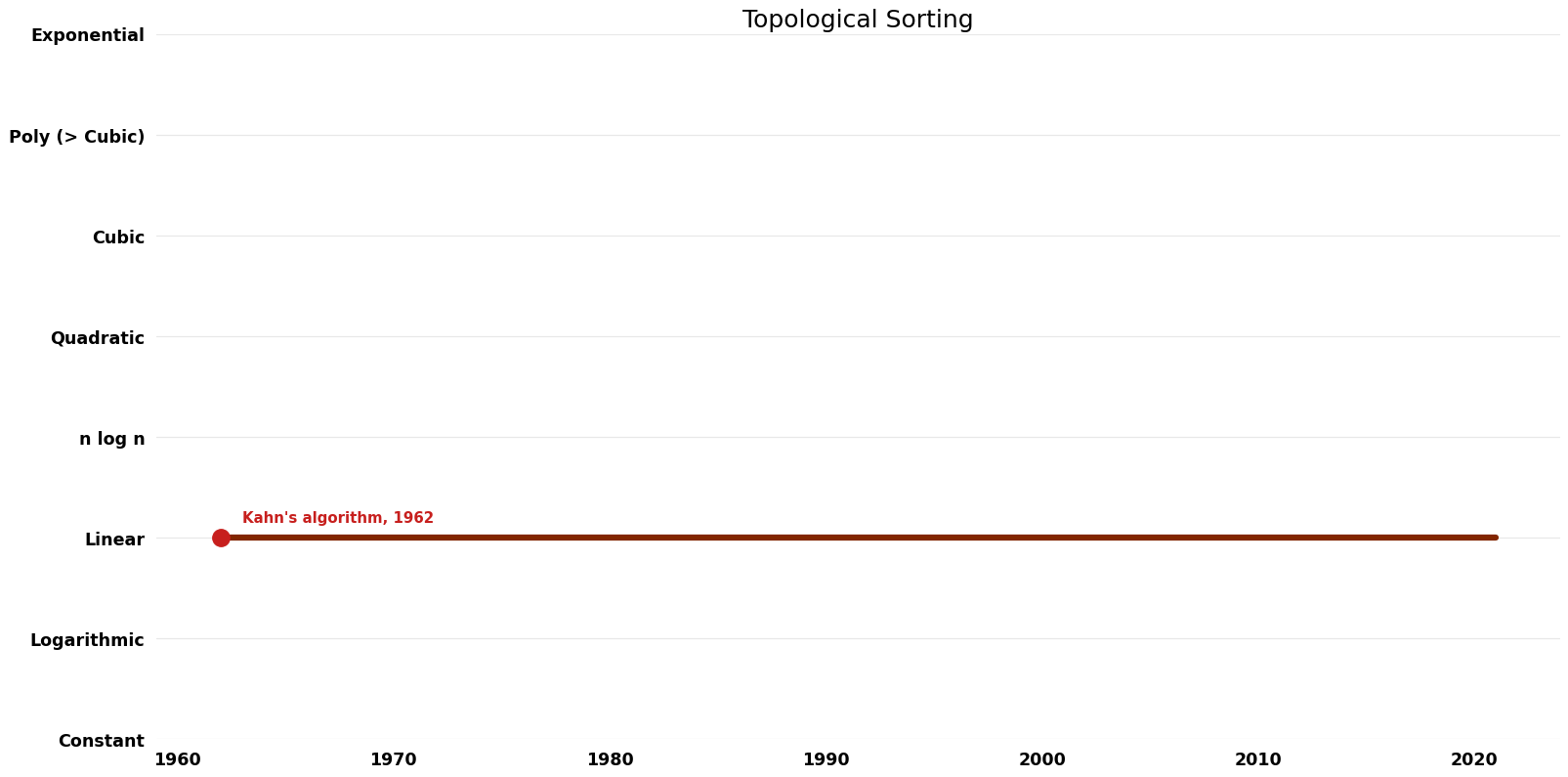
== Space Complexity graph == | |||
[[File:Topological Sorting - Space.png|1000px]] | |||
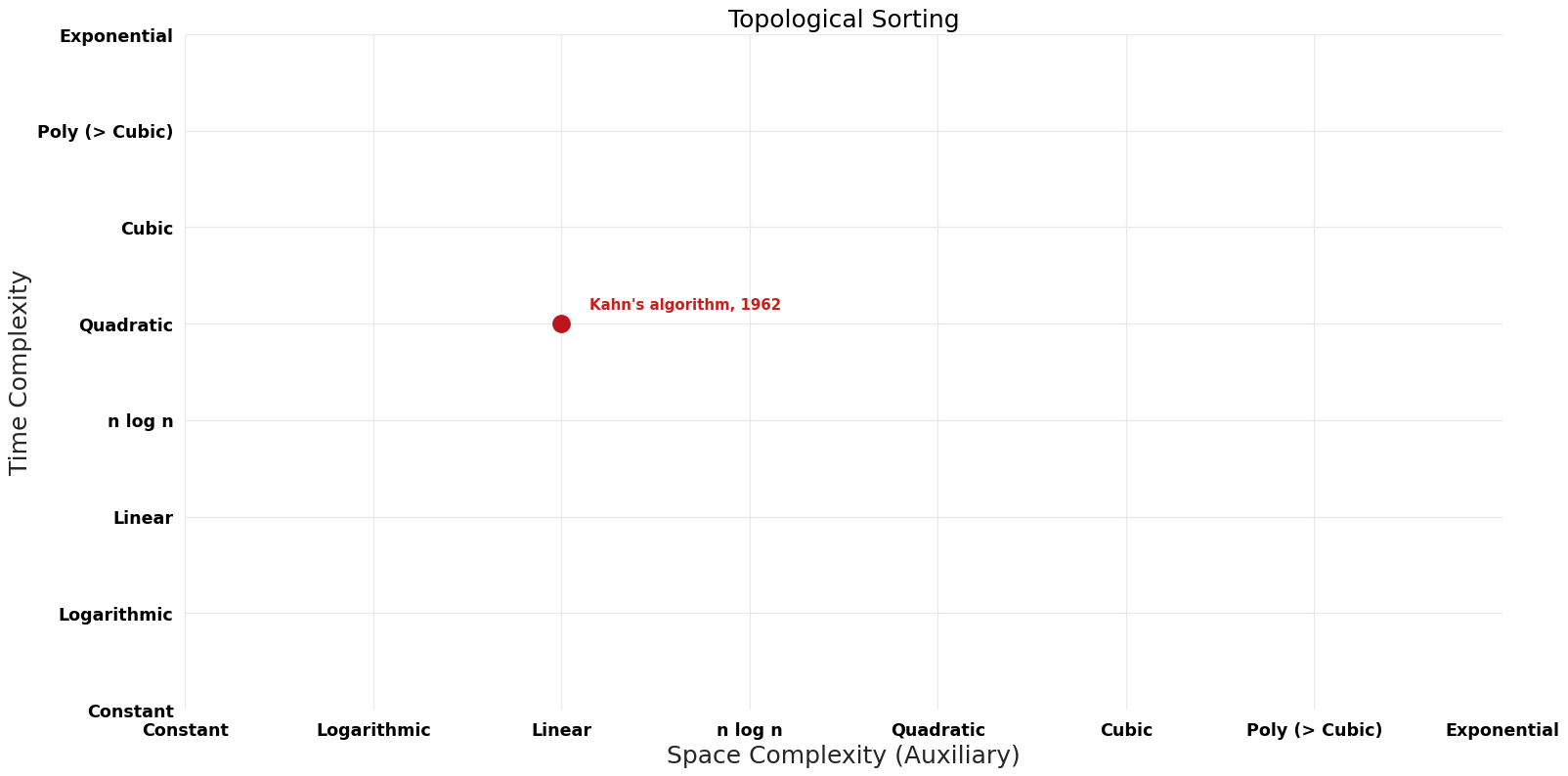
== Pareto Decades graph == | |||
[ | [[File:Topological Sorting - Pareto Frontier.png|1000px]] | ||
Revision as of 10:22, 15 February 2023
Description
Given a graph or network, find a topological sorting of the graph. A list in topological order has a special property. Simply expressed: proceeding from element to element along any path in the network, one passes through the list in one direction only. Stated another way, a list in topological order is such that no element appears in it until after all elements appearing on all paths leading to the particular element have been listed.
Parameters
V: number of vertices E: number of edges
Table of Algorithms
| Name | Year | Time | Space | Approximation Factor | Model | Reference |
|---|---|---|---|---|---|---|
| Kahn's algorithm | 1962 | $O(V+E)$ | $O(V)$ auxiliary | Exact | Deterministic | Time |
| Tarjan's DFS based algorithm | 1976 | $O(V+E)$ | $O(V)$ auxiliary? | Exact | Deterministic | Time |
| Dekel; Nassimi & Sahni Parallel Implementation | 1981 | $O( log² V)$ | $O(V^{2})$?? | Exact | Parallel | Time |
Time Complexity graph
Space Complexity graph
Pareto Decades graph
