Matrix Multiplication: Difference between revisions
Jump to navigation
Jump to search
(Created page with "== Problem Description== Matrix multiplication or multiplication of matrices is one of the operations that can be performed on matrices in linear algebra. Multiplication of matrix A with matrix B is possible when both the given matrices, A and B are compatible. Matrix multiplication is a binary operation, that gives a matrix from two given matrices. Matrix multiplication was first introduced in 1812 by French mathematician Jacques Philippe Marie Binet, in order to repre...") |
No edit summary |
||
| Line 1: | Line 1: | ||
== | {{DISPLAYTITLE:Matrix Multiplication (Matrix Product)}} | ||
== Description == | |||
Matrix | Matrix Multiplication or Matrix Product is a binary operation that produces a matrix from two matrices with entries in a field; or; more generally; in a ring or even a semiring. | ||
== | == Related Problems == | ||
Subproblem: [[Boolean Matrix Multiplication]], [[ Matrix Product Verification]] | |||
[[ | |||
Related: [[Boolean Matrix Multiplication (Combinatorial)]], [[Matrix Product Verification]], [[Distance Product]], [[$(\min, \leq)$ Product]] | |||
== Parameters == | |||
<pre>n: dimension of square matrix</pre> | |||
== Table of Algorithms == | |||
{| class="wikitable sortable" style="text-align:center;" width="100%" | |||
! Name !! Year !! Time !! Space !! Approximation Factor !! Model !! Reference | |||
|- | |||
[ Strassen's algorithm ( | | [[Naive algorithm (Matrix Multiplication Matrix Product)|Naive algorithm]] || 1940 || $O(n^{3})$ || $O({1})$ auxiliary || Exact || Deterministic || | ||
|- | |||
[http://www.cs. | | [[Strassen's algorithm (Matrix Multiplication Matrix Product)|Strassen's algorithm]] || 1969 || $O(n^{(log7/log2)}) ~ O(n^{2.{80}7})$ || $O(n^{2})$ || Exact || Deterministic || [https://link.springer.com/article/10.1007%2FBF02165411 Time] & [http://www.cs.cmu.edu/afs/cs/academic/class/15750-s17/ScribeNotes/lecture1.pdf Space] | ||
|- | |||
[ | | [[Pan's algorithm (Matrix Multiplication Matrix Product)|Pan's algorithm]] || 1978 || $O(n^{(log({143640})/log({70}))}) ~ O(n^{2.{79}5})$ || $O(n^{2})$ || Exact || Deterministic || [https://ieeexplore.ieee.org/document/4567976 Time] | ||
|- | |||
[https:// | | [[Romani's algorithm (Matrix Multiplication Matrix Product)|Romani's algorithm]] || 1981 || $O(n^{2.{5166}5})$ || $O(n^{2})$ || Exact || Deterministic || [https://epubs.siam.org/doi/abs/10.1137/0211020 Time] | ||
| | |- | ||
| [[Coppersmith–Winograd algorithm (Matrix Multiplication Matrix Product)|Coppersmith–Winograd algorithm]] || 1981 || $O(n^{2.{49554}8})$ || $O(n^{2})$ || Exact || Deterministic || [https://epubs.siam.org/doi/abs/10.1137/0211038 Time] | |||
|- | |||
| [[Strassen's algorithm (Matrix Multiplication Matrix Product)|Strassen's algorithm]] || 1986 || $O(n^{(log54/log5)}) ~ O(n^{({2.4785})})$ || $O(n^{2})$ || Exact || Deterministic || [https://ieeexplore.ieee.org/abstract/document/4568194 Time] | |||
|- | |||
| [[Coppersmith–Winograd algorithm (Matrix Multiplication Matrix Product)|Coppersmith–Winograd algorithm]] || 1990 || $O(n^{2.{375}5})$ || $O(n^{2})$ || Exact || Deterministic || [http://www.cs.umd.edu/~gasarch/TOPICS/ramsey/matrixmult.pdf Time] | |||
|- | |||
| [[Vassilevska Williams (Matrix Multiplication Matrix Product)|Vassilevska Williams]] || 2014 || $O(n^{2.{37287}3})$ || $O(n^{2})$ || Exact || Deterministic || [http://theory.stanford.edu/~virgi/matrixmult-f.pdf Time] | |||
|- | |- | ||
| | | [[François Le Gall (Matrix Multiplication Matrix Product)|François Le Gall]] || 2014 || $O(n^{2.{372863}9})$ || $O(n^{2})$ || Exact || Deterministic || [https://arxiv.org/abs/1401.7714 Time] | ||
| | |||
| | |||
|- | |- | ||
| | | [[Bini's algorithm (Matrix Multiplication Matrix Product)|Bini's algorithm]] || 1979 || $O(n^{2.{779}9})$ || $O(n^{2})$ || $O(n logn)$ error || Deterministic || [https://doi.org/10.1016/0020-0190(79)90113-3 Time] | ||
| | |||
| | |||
|- | |- | ||
| | | [[Schonhage's algorithm (Matrix Multiplication Matrix Product)|Schonhage's algorithm]] || 1980 || $O(n^{({3}*log52/log110)}) ~ O(n^{2.{521}8})$ || $O(n^{2})$ || ? || Deterministic || [https://epubs.siam.org/doi/abs/10.1137/0210032 Time] | ||
| | |||
| | |||
|- | |- | ||
| | |} | ||
| | |||
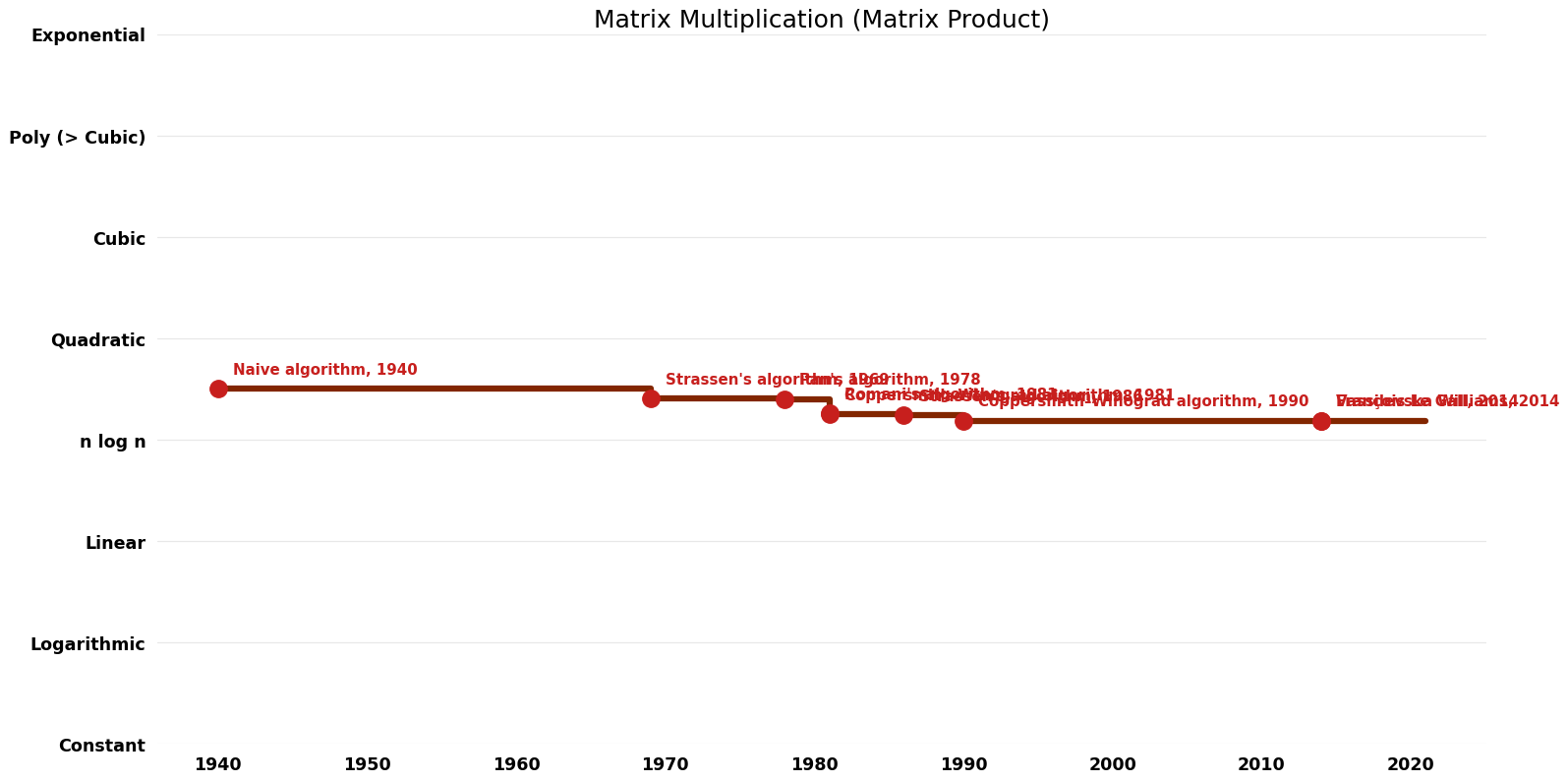
== Time Complexity graph == | |||
[[File:Matrix Product - Matrix Multiplication - Time.png|1000px]] | |||
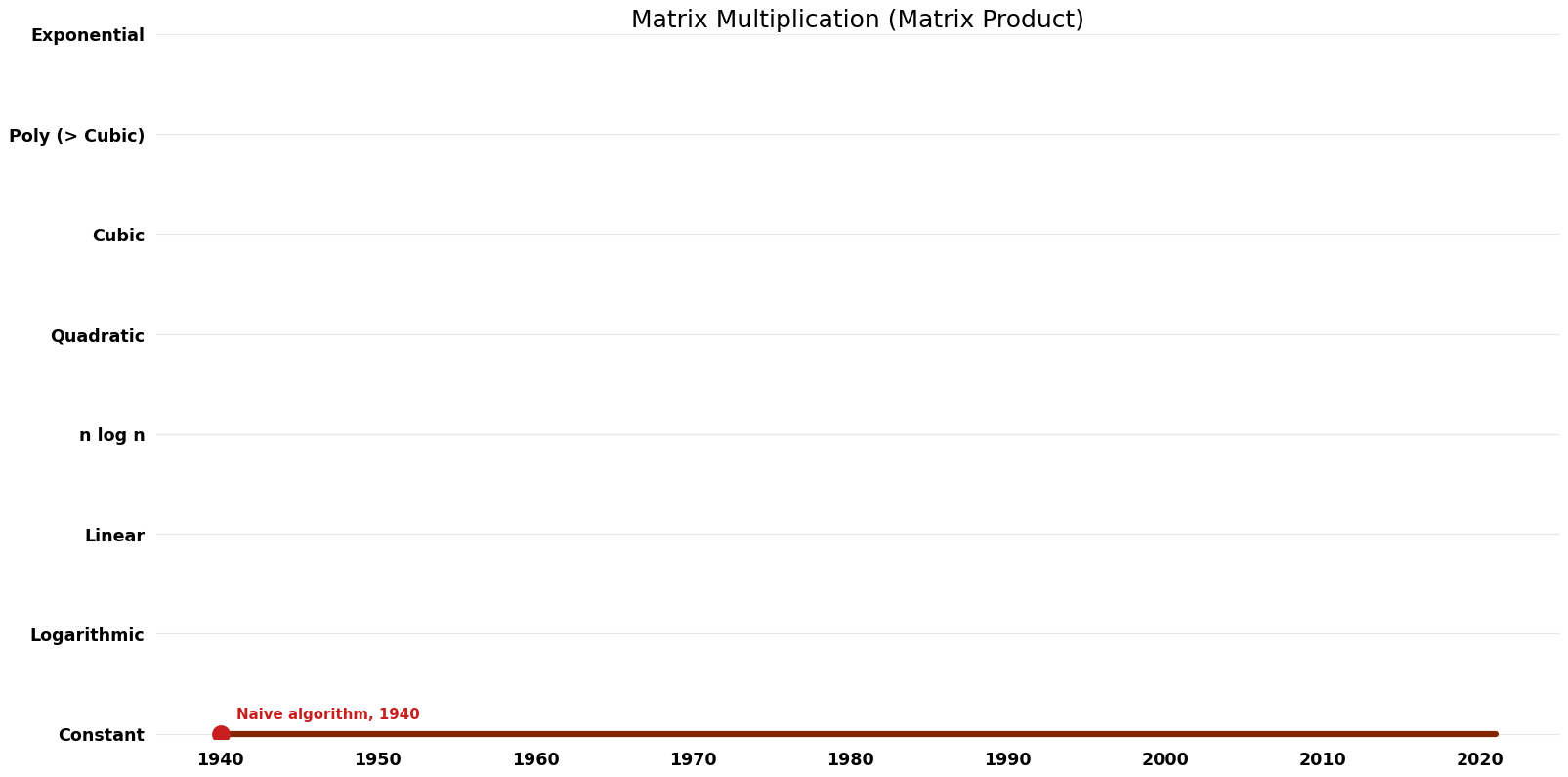
== Space Complexity graph == | |||
[[File:Matrix Product - Matrix Multiplication - Space.png|1000px]] | |||
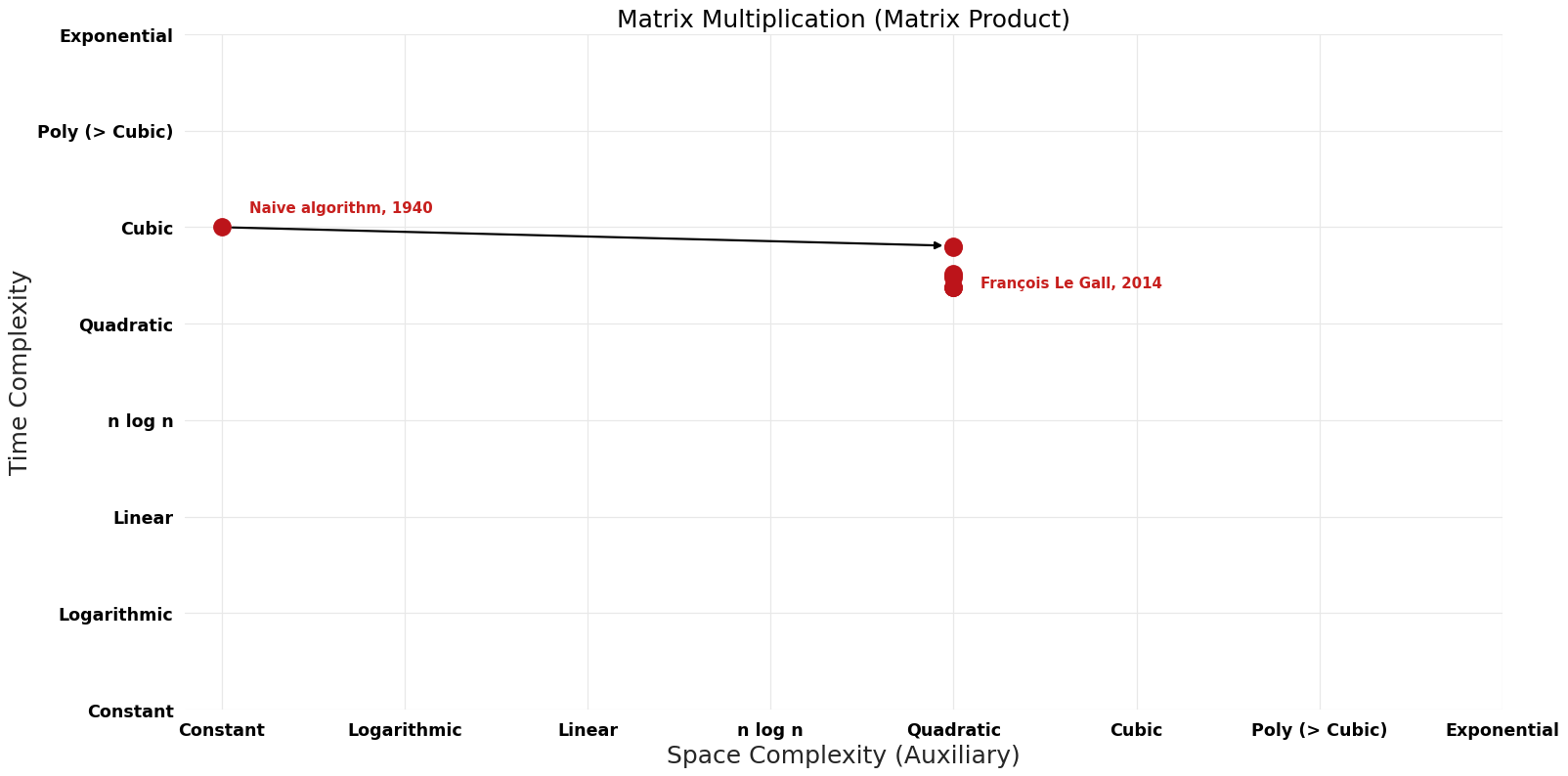
== Pareto Decades graph == | |||
[[File:Matrix Product - Matrix Multiplication - Pareto Frontier.png|1000px]] | |||
== References/Citation == | |||
https://arxiv.org/pdf/2010.05846.pdf | |||
Revision as of 11:18, 15 February 2023
Description
Matrix Multiplication or Matrix Product is a binary operation that produces a matrix from two matrices with entries in a field; or; more generally; in a ring or even a semiring.
Related Problems
Subproblem: Boolean Matrix Multiplication, Matrix Product Verification
Related: Boolean Matrix Multiplication (Combinatorial), Matrix Product Verification, Distance Product, $(\min, \leq)$ Product
Parameters
n: dimension of square matrix
Table of Algorithms
| Name | Year | Time | Space | Approximation Factor | Model | Reference |
|---|---|---|---|---|---|---|
| Naive algorithm | 1940 | $O(n^{3})$ | $O({1})$ auxiliary | Exact | Deterministic | |
| Strassen's algorithm | 1969 | $O(n^{(log7/log2)}) ~ O(n^{2.{80}7})$ | $O(n^{2})$ | Exact | Deterministic | Time & Space |
| Pan's algorithm | 1978 | $O(n^{(log({143640})/log({70}))}) ~ O(n^{2.{79}5})$ | $O(n^{2})$ | Exact | Deterministic | Time |
| Romani's algorithm | 1981 | $O(n^{2.{5166}5})$ | $O(n^{2})$ | Exact | Deterministic | Time |
| Coppersmith–Winograd algorithm | 1981 | $O(n^{2.{49554}8})$ | $O(n^{2})$ | Exact | Deterministic | Time |
| Strassen's algorithm | 1986 | $O(n^{(log54/log5)}) ~ O(n^{({2.4785})})$ | $O(n^{2})$ | Exact | Deterministic | Time |
| Coppersmith–Winograd algorithm | 1990 | $O(n^{2.{375}5})$ | $O(n^{2})$ | Exact | Deterministic | Time |
| Vassilevska Williams | 2014 | $O(n^{2.{37287}3})$ | $O(n^{2})$ | Exact | Deterministic | Time |
| François Le Gall | 2014 | $O(n^{2.{372863}9})$ | $O(n^{2})$ | Exact | Deterministic | Time |
| Bini's algorithm | 1979 | $O(n^{2.{779}9})$ | $O(n^{2})$ | $O(n logn)$ error | Deterministic | Time |
| Schonhage's algorithm | 1980 | $O(n^{({3}*log52/log110)}) ~ O(n^{2.{521}8})$ | $O(n^{2})$ | ? | Deterministic | Time |